Note này được dựa trên Concrete Mathematics, 3.3, và bài viết về bài toán Josephus trên CP-Algorithms .

Xét bài toán Josephus dạng tổng quát.

Cho ~n~ người đứng thành một vòng tròn, mỗi người được đánh số từ 1 đến ~n~. Bắt đầu từ vị trí số 1, mỗi người sẽ đếm lần lượt 1, 2, ..., ~k~, người đếm ~k~ sẽ bị loại khỏi vòng tròn, và mọi người tiếp tục đếm lại từ ~1~ cho đến khi chỉ còn lại một người. Hỏi người đánh số nào là người ở lại vòng tròn cuối cùng.

Một ý tưởng để giải quyết bài toán này là khi mỗi người đếm mà không bị loại, ta gán số thứ tự mới bằng số thứ tự lớn nhất hiện tại cộng ~1~. Ví dụ minh họa một vài lượt đếm với ~n = 10~, ~k = 3~

• Người ~1~ đếm ~1~ và không bị loại, ta gán số thứ tự mới ~11~ (kí hiệu ~1 \rightarrow 11~)
• Người ~2~ đếm ~2~ và không bị loại, ta gán số thứ tự mới ~12~ (kí hiệu ~2 \rightarrow 12~)
• Người ~3~ đếm ~3~ và bị loại, ta không gán số thứ tự mới (kí hiệu ~3 \rightarrow \emptyset~)
• ~4 \rightarrow 13~
• ~5 \rightarrow 14~
• ~6 \rightarrow \emptyset~
• ...

Ta thấy người bị loại sẽ có số thứ tự lần lượt là ~k~, ~2k~, .... Do cuối cùng cả ~n~ người bị loại, người bị loại cuối cùng sẽ có số thứ tự ~nk~.

Để các công thức tính toán sau này, ta sẽ đánh số lại mọi người theo thứ tự từ ~nk~ về ~1~. Ví dụ, khi ~n = 10~, ~k = 3~ thì ban đầu ~n~ người sẽ có số thứ tự lần lượt là ~30, 29, 28, ..., 21~. Một vài lượt chơi ban đầu như sau:

• ~30 \rightarrow 20~
• ~29 \rightarrow 19~
• ~28 \rightarrow \emptyset~
• ~27 \rightarrow 18~
• ~26 \rightarrow 17~
• ~25 \rightarrow \emptyset~

Người ở lại vòng tròn cuối cùng sẽ có số thứ tự cuối cùng là ~1~. Giờ ta chỉ cần tìm lại số thứ tự ban đầu của người này là giải quyết được bài toán.

Giả sử ~x~ là số thứ tự của một người nào đó trong vòng tròn. Khi tìm số thứ tự trước đó của người ~x~, kí hiệu là ~x'~, ta sẽ cần xử lí hai trường hợp:

• Nếu ~x \geq nk - n + 1~ thì ~x~ là số thứ tự ban đầu, vì thế sẽ không có số thứ tự trước đó.
• Trường hợp ~x < nk - n + 1~, ta có thể chia các số từ ~nk~ đến ~1~ thành những nhóm ~k~ số liên tiếp nhau (gọi tắt là nhóm ~k~, minh họa bằng cách đóng khung chữ nhật), và chia các số từ ~nk - n~ đến ~1~ thành những nhóm ~k-1~ số liên tiếp nhau (gọi tắt là nhóm ~k-1~, minh họa bằng cách khoanh tròn).

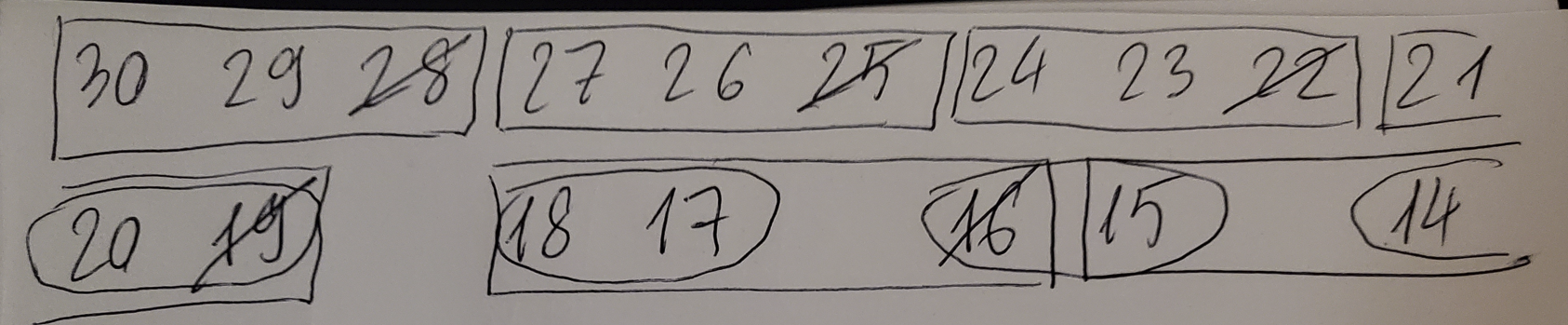
Đánh số các nhóm theo thứ tự từ ~0~. Trong nội bộ mỗi nhóm, ta cũng đánh số thứ tự từ ~0~.

Với mọi ~x < nk - n + 1~, nếu ~x~ là số thứ ~i~ nhóm ~k-1~ thứ ~j~ thì ~x'~ là số thứ ~i~ của nhóm ~k~ thứ ~j~ (dễ thấy điều này ở một số số ~x~ ngay sau số ~nk - n + 1~, cỏn các số sau nữa thì ta có thể chứng minh bằng quy nạp được). Vậy ta chỉ cần tìm ~i~ và ~j~ là ra ~x'~.

Ta tính được:

~x~ thuộc nhóm ~k-1~ thứ ~\lfloor \frac{nk - n - x}{k-1} \rfloor~

Số thứ tự của ~x~ trong nhóm ~k-1~ là ~nk - n - x - (k-1)\lfloor \frac{nk - n - x}{k-1} \rfloor~

~x'~ sẽ là số thứ ~nk - n - x - (k-1)\lfloor \frac{nk - n - x}{k-1} \rfloor~ của nhóm ~k~ thứ ~\lfloor \frac{nk - n - x}{k-1} \rfloor~, vậy

~x' = nk - k\lfloor \frac{nk - n - x}{k-1} \rfloor - (nk - n - x - (k-1)\lfloor \frac{nk - n - x}{k-1} \rfloor)~

~x' = n + x - \lfloor \frac{n(k - 1) - x}{k-1} \rfloor~

~x' = n + x - \lfloor n - \frac{x}{k-1} \rfloor~

Vận dụng tính chất ~\lfloor x + y \rfloor = x + \lfloor y \rfloor~ khi ~x \in \mathbb{Z}~ để đưa ~n~ ra ngoài hàm làm tròn xuống, ta có:

~x' = x - \lfloor -\frac{x}{k-1} \rfloor~

Vận dụng tiếp tính chất ~\lfloor -x \rfloor = -\lceil x \rceil~, ta có:

~x' = x + \lceil \frac{x}{k-1} \rceil~

~x' = \lceil \frac{x(k-1)}{k-1} + \frac{x}{k-1} \rceil~

~\boxed{x' = \lceil \frac{k}{k-1} x \rceil}~

Từ hai trường hợp trên, ta ra được thuật toán sau để tìm số thứ tự của người ở lại vòng tròn cuối cùng

Đọc n, k
Gán x = 1
While x < nk - k + 1:
    x = ceil(k/(k-1) * x)

# x là số thứ tự ban đầu nếu ta đánh số ngược, ta cần tìm số thứ tự ban đầu khi đánh số thuận
Gán x = nk + 1 - x
In ra x

Thuật toán trên có độ phức tạp ~O(\log_{\frac{k}{k-1}}(nk))~. Với ~k = 10^5, n = 10^{18}~, thuật toán này sẽ chỉ tốn khoảng ~6 \times 10^7~ phép tính và hoàn toàn có thể chạy dưới ~1~ giây, trong khi thuật toán duyệt thông thường sẽ mất đến ~O(nk)~ phép tính (hay khoảng ~10^{17}~ phép tính)

Vậy là ta đã giải quyết được bài toán trong trường hợp ~n~ lớn, ~k~ khá lớn. Vậy nếu như ta phải giải bài toán trong trường hợp ~k~ lớn, ~n~ khá lớn thì ta làm thế nào?

Gọi ~J_{n,k}~ là người ở lại vòng tròn cuối cùng nếu ta đánh số các người chơi từ ~0~ đến ~n-1~. Ta mô phỏng lại trò chơi bằng máy tính với một số giá trị ~n, k~ nhỏ rồi lập bảng. Ta sẽ thấy được quy luật

~J_{n, k} = (J_{n-1, k} + k) \text{ mod } n~

Từ công thức này, ta sẽ tính được ~J_{n,k}~ với độ phức tạp ~O(n)~, không phụ thuộc vào ~k~

Rất tiếc là ở thời điểm hiện tại, các nhà khoa học máy tính vẫn chưa tìm ra được cách giải quyết "dưới 1 giây" của bài toán này trong trường hợp cả ~n~ và ~k~ đều rất lớn.