Dựa trên Concrete Mathematics, 3.1

1. Làm tròn lên, làm tròn xuống

Ta định nghĩa các kí hiệu sau:

~\lfloor x \rfloor~ - số nguyên lớn nhất không vượt quá ~x~. Kí hiệu này đọc là "phần nguyên của ~x~" hoặc "~x~ làm tròn xuống"

Ví dụ: ~\lfloor 1.2 \rfloor = 1, \lfloor -0.8 \rfloor = -1~.

Lưu ý rằng với số âm thì các ngôn ngữ lập trình khác nhau có thể định nghĩa "làm tròn xuống khác nhau", ta sẽ thống nhất sử dụng định nghĩa trên cho dễ biến đổi.

~\lceil x \rceil~ - số nguyên nhỏ nhất không nhỏ hơn ~x~. Kí hiệu này đọc là "~x~ làm tròn lên"

Ví dụ: ~\lceil 1.2 \rceil = 2, \lceil -0.8 \rceil = 0~

Để dễ nhìn tính chất của hai hàm làm tròn, ta vẽ đồ thị các hàm số ~y = \lfloor x \rfloor, y = \lceil x \rceil~ và ~y = x~ trên cùng một hệ trục tọa độ

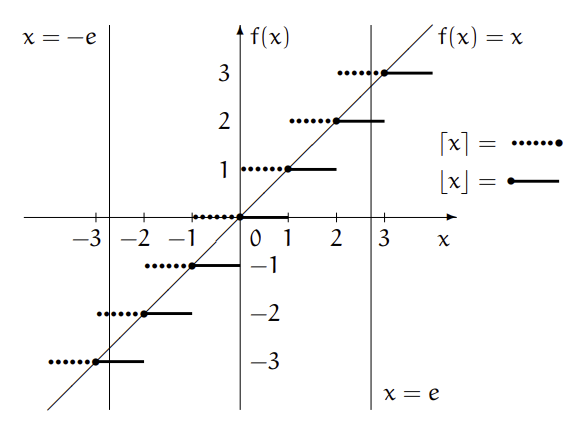
Dễ thấy:

~x = \lfloor x \rfloor \Leftrightarrow x \in \mathbb{Z} \Leftrightarrow x = \lceil x \rceil~

~\lceil x \rceil - \lfloor x \rfloor = [x \in \mathbb{Z}]~

~x - 1 < \lfloor x \rfloor \leq x \leq \lceil x \rceil < x + 1~

Ta thấy khi lấy đối xứng đồ thị hàm số ~y = \lfloor x \rfloor~ thì ta được ~y = \lceil x \rceil~, vì thế nên:

~\lfloor -x \rfloor = - \lceil x \rceil~ và ~\lceil -x \rceil = - \lfloor x \rfloor~

Ngoài ra

~\lfloor x \rfloor = n \Leftrightarrow n \leq x < n+1 \Leftrightarrow x-1 < n \leq x-1~

~\lceil x \rceil = n \Leftrightarrow n-1 < x \leq n \Leftrightarrow x \leq n < x+1~

Ta có thể cộng một số nguyên ở trong hay ở ngoài hàm làm tròn lên lẫn làm tròn xuống

~\lfloor x + n \rfloor = \lfloor x \rfloor + n~ với ~n \in \mathbb{Z}~

~\lceil x + n \rceil = \lceil x \rceil + n~ với ~n \in \mathbb{Z}~

Lưu ý điều này không đúng với phép nhân (~\lfloor nx \rfloor \ne n \lfloor x \rfloor~ sai khi ~n = 2~ và ~x = \frac{1}{2}~)

Với ~n~ là số nguyên, ta cũng dễ dàng chứng minh được các phép biến đổi tương đương sau:

~x < n \Leftrightarrow \lfloor x \rfloor < n~

~n < x \Leftrightarrow n < \lceil x \rceil~

~x \leq n \Leftrightarrow \lfloor x \rfloor \leq n~

~n \leq x \Leftrightarrow n \leq \lceil x \rceil~

Người ta còn định nghĩa ~\{x\} = x - \lfloor x \rfloor~ (~\{x\}~ được đọc là "phần thập phân của ~x~"). Nếu một số thực ~x = n + \theta~ với ~n, \theta~ thỏa mãn ~n~ nguyên và ~0 \leq \theta < 1~ thì ta biết được ~n = \lfloor x \rfloor~ và ~\theta = \{x\}~

2. Bài tập ứng dụng

Ví dụ 1:

Sử dụng khái niệm phần thập phân và tính chất ~\lfloor x + n \rfloor = \lfloor x \rfloor + n~ với ~n \in \mathbb{Z}~, ta có thể chứng minh được tính chất sau:

~\lfloor x + y \rfloor~ chỉ có thể là ~\lfloor x \rfloor + \lfloor y \rfloor~ hoặc ~\lfloor x \rfloor + \lfloor y \rfloor + 1~

Ta có:

~\lfloor x + y \rfloor = \lfloor \lfloor x \rfloor + \{x\} + \lfloor y \rfloor + \{y\} \rfloor = \lfloor x \rfloor + \lfloor y \rfloor + \lfloor \{x\} + \{y\} \rfloor~

Do ~0 \leq \{x\}, \{y\} < 1~ nên ~0 \leq \{x\} + \{y\} < 2~, và vì thế nên ~\lfloor \{x\} + \{y\} \rfloor~ chỉ có thể là ~0~ hoặc ~1~.

Nếu ~\lfloor \{x\} + \{y\} \rfloor = 0~, ~\lfloor x + y \rfloor = \lfloor x \rfloor + \lfloor y \rfloor~

Nếu ~\lfloor \{x\} + \{y\} \rfloor = 1~, ~\lfloor x + y \rfloor = \lfloor x \rfloor + \lfloor y \rfloor + 1~

Ví dụ 2:

Tính ~\lfloor \lg 35 \rfloor~ (do độ phổ biến của logarithm cơ số 2 trong Tin học, ta kí hiệu ~\log_2~ bằng ~\lg~)

Ta có:

~2^5 \leq 35 < 2^6 \Rightarrow 5 \leq \lg 35 < 6 \Rightarrow \lfloor \lg 35 \rfloor = 5~

Ví dụ 3:

Cho hàm ~f~ liên tục và đồng biến thỏa mãn ~f(x) \in \mathbb{Z} \Rightarrow x \in \mathbb{Z}~.

Khi đó, ~\lfloor f(x) \rfloor = \lfloor f(\lfloor x \rfloor) \rfloor~.

Tương tự, ta cũng có ~\lceil f(x) \rceil = \lceil f(\lceil x \rceil) \rceil~

Chứng minh:

Đặt ~m = \lfloor f(\lfloor x \rfloor) \rfloor~.

Khi đó ~m \leq f(\lfloor x \rfloor) < m+1~ (phá dấu làm tròn xuống ở ngoài bằng định nghĩa)

Do ~x \geq \lfloor x \rfloor~ và ~f~ đồng biến, ta có ~f(x) \geq f(\lfloor x \rfloor) \Rightarrow f(x) \geq m~

Để chứng minh ~\lfloor f(x) \rfloor = m~, ta giờ chỉ cần chứng minh ~f(x) < m+1~. Ta sẽ chứng minh điều này bằng phản chứng.

Giả dụ ~f(x) \geq m+1~.

Khi đó do ~\begin{cases} f(\lfloor x \rfloor) < m+1 \leq f(x) \\ f \text{ liên tục} \end{cases}~, theo định lí giá trị trung gian, ta sẽ tìm được ~c~ thỏa mãn ~f(c) = m+1~ và ~\lfloor x \rfloor < c \leq x~

Theo giả thiết ~f(x) \in \mathbb{Z} \Rightarrow x \in \mathbb{Z}~, do ~f(c) = m+1 \in \mathbb{Z}~, ~c \in \mathbb{Z}~.

Như vậy, ta tìm được số nguyên ~c~ nằm giữa ~\lfloor x \rfloor~ và ~x~, nhưng lại không bằng ~\lfloor x \rfloor~. Điều này vô lí.

Do đó giả dụ ban đầu sai, nói cách khác, ~f(x) < m+1~ đúng.

Kết hợp ~\begin{cases} m \leq f(x) \\ f(x) < m+1 \end{cases}~, ta có ~\lfloor f(x) \rfloor = m \Rightarrow \lfloor f(x) \rfloor = \lfloor f(\lfloor x \rfloor) \rfloor~. Đây là điều phải chứng minh.

Hệ quả của ví dụ 3:

~\lfloor \sqrt{x} \rfloor = \lfloor \sqrt{\lfloor x \rfloor} \rfloor~

~\lfloor \frac{x + m}{n} \rfloor = \lfloor \frac{\lfloor x \rfloor + m}{n} \rfloor~ (~n~ dương)

Các công thức tương tự với hàm làm tròn lên cũng đúng

Ví dụ 4: Giải phương trình ẩn ~x~ sau: ~\lceil \sqrt{\lfloor x \rfloor} \rceil = \lceil \sqrt{x} \rceil~

Xét các trường hợp sau:

Trường hợp 1: ~\sqrt{x}~ nguyên, ~\sqrt{\lfloor x \rfloor}~ nguyên. Khi đó phương trình luôn đúng. Kết hợp điều kiện, ta được ~x = m^2~ với ~m \in \mathbb{Z}~

Trường hợp 2: ~\sqrt{x}~ nguyên, ~\sqrt{\lfloor x \rfloor}~ không nguyên. Trường hợp này không thể xảy ra. ~\sqrt{x}~ nguyên ~\Rightarrow x~ nguyên ~\Rightarrow \lfloor x \rfloor = x \Rightarrow \sqrt{\lfloor x \rfloor} = \sqrt{x}~ nguyên.

Trường hợp 3: ~\sqrt{x}~ không nguyên, ~\sqrt{\lfloor x \rfloor}~ nguyên. Khi đó, phương trình trở thành

~\sqrt{\lfloor x \rfloor} = \lfloor \sqrt{x} \rfloor + 1 \Leftrightarrow \sqrt{\lfloor x \rfloor} = \lfloor \sqrt{\lfloor x \rfloor} \rfloor + 1 > (\sqrt{\lfloor x \rfloor} - 1) + 1 \Leftrightarrow \sqrt{\lfloor x \rfloor} > \sqrt{\lfloor x \rfloor}~ (vô nghiệm)

Trường hợp 4: ~\sqrt{x}~ không nguyên, ~\sqrt{\lfloor x \rfloor}~ không nguyên. Khi đó, phương trình trở thành

~\lfloor \sqrt{\lfloor x \rfloor} \rfloor + 1 = \lfloor \sqrt{x} \rfloor + 1 \Leftrightarrow \lfloor \sqrt{\lfloor x \rfloor} \rfloor = \lfloor \sqrt{x} \rfloor~ (luôn đúng)

Kết hợp điều kiện, ta được ~\lfloor x \rfloor \ne m^2~ với ~m \in \mathbb{Z}~ (phần nguyên của ~x~ không là số chính phương)

Từ bốn trường hợp trên, ta kết luận tập nghiệm của phương trình ~\lceil \sqrt{\lfloor x \rfloor} \rceil = \lceil \sqrt{x} \rceil~ là

~S = \{m \in \mathbb{Z} | m^2\} \cup \{x \in \mathbb{R} | \forall m \in \mathbb{Z}: \lfloor x \rfloor \ne m^2 \}~

(số ~x~ là nghiệm của phương trình khi và chỉ khi ~x~ là số chính phương hoặc phần nguyên của ~x~ không là số chính phương)