Tạp chí VNOI Xuân Bính Ngọ - Bài toán cây khung Manhattan nhỏ nhất của tập điểm nguyên có tọa độ nhỏ
Một thuật toán đơn giản giải bài toán cây khung Manhattan nhỏ nhất của tập điểm nguyên có tọa độ nhỏ
Tác giả: Bùi Việt Dũng - Học viên Nghiệp vụ Sư phạm tại Trường Đại học Vinh.
Giới thiệu
Bài toán tìm cây khung Manhattan nhỏ nhất có nội dung như sau:
Cho một tập ~P~ gồm ~n~ điểm có tọa độ nguyên trên mặt phẳng tọa độ, điểm thứ ~i~ có tọa độ ~(x_i, y_i)~. Ta cần nối các điểm này với nhau bằng các đoạn thẳng sao cho:
- Một điểm bất kì trong tập ~P~ có thể đi đến tất cả các điểm khác trong tập ~P~ bằng các đoạn thẳng đã nối. Ta phải đi hết đoạn thẳng, không được phép "nhảy" từ đoạn thẳng này sang đoạn thẳng khác tại một điểm không nằm trong tập ~P~.
- Tổng chi phí các đoạn nối là nhỏ nhất có thể. Chi phí một đoạn nối từ điểm ~(x_u, y_u)~ đến điểm ~(x_v, y_v)~ được tính bằng khoảng cách Manhattan, tức ~|x_u - x_v| + |y_u - y_v|~ thay vì tính bằng khoảng cách Euclide thông thường (~\sqrt{(x_u - x_v)^2 + (y_u - y_v)^2}~)
Ở bài viết này, tôi sẽ giới thiệu một thuật toán ~\mathcal{O}(xy + n \log n)~ có khả năng giải quyết các bộ dữ liệu có ~n \leq 10^5~ và ~0 \leq x, y < 1000~ của bài toán trên trong giới hạn thời gian 1 giây. Điều này đồng nghĩa với việc ta giải quyết được subtask 3 tương ứng với ~20\%~ số điểm của Bài 3 - Kết nối Internet của Kỳ thi chọn Học sinh Giỏi Quốc gia môn Tin học năm học 2021-2022 (VOI 2022).
Trong video chữa đề VOI 2022, VNOI cũng đã giới thiệu một thuật toán giải quyết subtask này. Tuy nhiên, theo cảm nhận chủ quan của tôi, thuật toán được giới thiệu ở bài viết này dễ cài đặt hơn, chỉ cần một số kĩ thuật cơ bản trên mảng hai chiều, thuật toán tìm kiếm theo chiều rộng (BFS) và thuật toán Kruskal.
Thuật toán của bài viết ít được chú ý trong lập trình thi đấu do tồn tại một thuật toán cài đặt phức tạp hơn, giải quyết được trọn vẹn bài toán trong ~\mathcal{O}(n \log n)~ (không phụ thuộc vào ~x, y~). Tuy nhiên, với hình thức chấm thi một lần duy nhất như hầu hết các kỳ thi Học sinh Giỏi tại Việt Nam hiện nay, sự tồn tại của thuật toán tìm cây khung Manhattan nhỏ nhất trong ~\mathcal{O}(xy + n\log n)~ vẫn có giá trị nhất định đối với người ra đề và thí sinh. Người ra đề có thể dùng thuật toán này làm căn cứ tạo subtask đơn giản cho những bài toán liên quan đến cây khung Manhattan nhỏ nhất, còn thí sinh có thể cài đặt thuật toán để giải quyết subtask, qua đó tạo đà tâm lý và làm căn cứ kiểm thử trước khi chinh phục trọn vẹn bài toán.
Thuật toán
- Nhân đôi tọa độ các điểm trong tập ~P~ để đơn giản hóa việc cài đặt.
- Với ~(x, y)~ là cặp số nguyên không âm có giá trị nhỏ hơn ~2000~, gọi ~\texttt{voronoi[x][y]}~ là chỉ số của điểm trong tập ~P~ mà gần điểm ~(x, y)~ nhất theo khoảng cách Manhattan. Ta có thể tính mảng hai chiều ~\texttt{voronoi}~ bằng cách BFS đa nguồn với các nguồn là ~n~ điểm trong tập ~P~ và chỉ di chuyển từ một điểm đến các điểm có khoảng cách Manhattan bằng ~1~. Sau khi thực hiện BFS, ta chia được các điểm nguyên thành các vùng như trong hình dưới đây.
Hình minh họa kết quả BFS trong trường hợp ~P = \{(0, 0); (0, 10); (2, 14); (4, 18)\}~, các điểm trong tập ~P~ được đánh chỉ số từ ~0~ theo thứ tự đã liệt kê. - Xây dựng tập cạnh có trọng số ~E~ sao cho mỗi cạnh ~(u, v)~ của tập thể hiện rằng vùng được đánh dấu bằng chỉ số ~u~ giáp với vùng được đánh dấu bằng chỉ số ~v~ và trọng số của cạnh là khoảng cách Manhattan giữa hai điểm ~P[u]~ và ~P[v]~. Ta làm điều này bằng cách duyệt mảng ~\texttt{voronoi}~ bằng hai vòng lặp lồng nhau để tìm các cặp hai điểm ~(x_1, y_1)~ và ~(x_2, y_2)~ có khoảng cách Manhattan bằng 1 ("ô" ~(x_1, y_1)~ và "ô" ~(x_2, y_2)~ có chung cạnh) mà ~\texttt{voronoi}[x_1][y_1] \ne \texttt{voronoi}[x_2][y_2]~. Với mỗi cặp điểm như vậy, ta thêm cạnh ~(\texttt{voronoi}[x_1][y_1], \texttt{voronoi}[x_2][y_2])~ kèm trọng số phù hợp vào tập ~E~.
- Thực hiện thuật toán Kruskal trên tập cạnh ~E~, ta thu được một cây khung.
- Chia đôi trọng số của các cạnh trong cây khung này, ta sẽ có được cây khung Manhattan của tập điểm ~P~ ban đầu.
Cài đặt
Đoạn code sau được sử dụng để giải quyết bài toán Grid MST trên Kattis.
#include <bits/stdc++.h>
using namespace std;
typedef pair<int, int> pii;
const int MAX_POINTS = 100000;
const int GRID_SIZE = 2000;
int numberOfPoints;
int pointX[MAX_POINTS], pointY[MAX_POINTS];
set<pii> existingPoints;
int voronoi[GRID_SIZE][GRID_SIZE];
// hai mảng này giúp dịch chuyển theo 4 hướng Đông - Tây - Nam - Bắc
int moveX[4] = {0,0,1,-1};
int moveY[4] = {1,-1,0,0};
queue<pii> bfsQueue;
bool withinLimit(int x,int y) {
return (0<=x and x<GRID_SIZE and 0<=y and y<GRID_SIZE);
}
struct Edge {
int u, v, weight;
};
vector<Edge> edges;
int parent[MAX_POINTS];
// cấu trúc dữ liệu các tập rời nhau (disjoint set union - DSU)
// tìm hiểu về DSU tại https://wiki.vnoi.info/algo/data-structures/disjoint-set-union
// tìm đỉnh cha (đỉnh đại diện) cho một tập đỉnh
int find_parent(int pointX) {
if (parent[pointX] == pointX) return pointX;
return parent[pointX] = find_parent(parent[pointX]);
}
// ghép tập đỉnh chứa đỉnh pointX và tập đỉnh chứa đỉnh pointY với nhau
void merge(int pointX,int pointY) {
parent[find_parent(pointX)] = find_parent(pointY);
}
int main() {
ios_base::sync_with_stdio(0); cin.tie(0);
cin >> numberOfPoints;
// đánh dấu tất cả các ô (điểm nguyên) đều không thuộc vùng nào
for (int i = 0; i < GRID_SIZE; ++i)
for (int j = 0; j < GRID_SIZE; ++j)
voronoi[i][j] = numberOfPoints+1;
for (int i = 0; i < numberOfPoints; ++i) {
cin >> pointX[i] >> pointY[i];
// nhân đôi tọa độ mỗi điểm để dễ cài đặt
pointX[i] *= 2;
pointY[i] *= 2;
// khi có nhiều điểm giống nhau, chỉ xét điểm đầu tiên
if (!existingPoints.count({pointX[i], pointY[i]})) {
existingPoints.insert({pointX[i], pointY[i]});
voronoi[pointX[i]][pointY[i]] = i;
bfsQueue.push({pointX[i], pointY[i]});
}
}
// thực hiện BFS đa nguồn để tạo các vùng
while (!bfsQueue.empty()) {
auto current = bfsQueue.front(); bfsQueue.pop();
int currentIndex = voronoi[current.first][current.second];
for (int direction = 0; direction < 4; ++direction) {
int neighborX = current.first + moveX[direction];
int neighborY = current.second + moveY[direction];
if (withinLimit(neighborX, neighborY) and
voronoi[neighborX][neighborY] == numberOfPoints+1) {
voronoi[neighborX][neighborY] = currentIndex;
bfsQueue.push({neighborX, neighborY});
}
}
}
// tìm các vùng kề nhau để tạo tập cạnh
for (int i = 0; i < GRID_SIZE; ++i)
for (int j = 0; j < GRID_SIZE; ++j) {
for (int direction = 0; direction < 4; ++direction) {
int neighborI = i + moveX[direction], neighborJ = j + moveY[direction];
if (withinLimit(neighborI, neighborJ) and
voronoi[i][j] != voronoi[neighborI][neighborJ]) {
int u = voronoi[i][j];
int v = voronoi[neighborI][neighborJ];
int weight = abs(pointX[u] - pointX[v]) + abs(pointY[u] - pointY[v]);
edges.push_back({u, v, weight});
}
}
}
// thực hiện thuật toán Kruskal
sort(edges.begin(), edges.end(), [&](Edge a, Edge b) { return a.weight < b.weight; });
// khởi tạo disjoint set union
// với mỗi i từ 0 đến numberOfPoints - 1, parent[i] <- i
iota(parent, parent + numberOfPoints, 0);
long long mstWeight = 0;
for (auto e: edges) {
if (find_parent(e.u) != find_parent(e.v)) {
merge(e.u, e.v);
mstWeight += (long long) e.weight;
}
}
// chia đôi vì đã nhân đôi tọa độ các điểm
cout << mstWeight / 2;
return 0;
}
Độ phức tạp của code này thực tế là ~\mathcal{O}(xy\log(xy))~, do danh sách cạnh edges có thể chứa nhiều cạnh trùng nhau. Ta có thể chứng minh được danh sách cạnh edges chứa tối đa ~\mathcal{O}(n)~ cạnh phân biệt, nhờ đó, khi sử dụng thêm cấu trúc dữ liệu unordered_set, ta giảm độ phức tạp của code xuống ~\mathcal{O}(xy + n \log n)~.
Giải thích tính đúng đắn của thuật toán
Đây là một thuật toán đơn giản. Tuy nhiên, việc chứng minh tính đúng đắn của nó khá phức tạp, đòi hỏi kiến thức liên quan đến sơ đồ Voronoi và lưới Delaunay. Chúng ta hãy cùng tìm hiểu những kiến thức đó trong bài viết này.
Sơ đồ Voronoi
Với tập điểm ~P = \{P_1; P_2; \dots; P_n\}~, ta định nghĩa vùng Voronoi (Voronoi region) của điểm ~P_i~ là tập hợp
với ~d(A, B)~ là khoảng cách giữa hai điểm ~A~ và ~B~.
Nói cách khác, vùng Voronoi của điểm ~P_i~ là một hình gồm các điểm gần điểm ~P_i~ hơn bất cứ điểm nào khác trong tập ~P~.
~d~ có thể là bất cứ hàm khoảng cách nào, miễn là thỏa mãn đồng thời các tính chất sau:
- ~\forall X, Y: d(X, Y) \geq 0~. Đẳng thức xảy ra khi và chỉ khi ~X = Y~.
- ~\forall X, Y: d(X, Y) = d(Y, X)~.
- ~\forall X, Y, Z: d(X, Y) + d(Y, Z) \geq d(X, Z)~ (bất đẳng thức tam giác).
Ở bài toán của bài viết này, ta sử dụng khoảng cách Manhattan. Ta có thể dễ dàng chứng minh khoảng cách Manhattan thỏa mãn tính chất 1 và 2. Do đó, ở bài viết này, tôi sẽ chỉ chứng minh khoảng cách Manhattan thỏa mãn tính chất 3 - bất đẳng thức tam giác.
Chứng minh
Chọn ba điểm ~X(x_1, x_2), Y(y_1, y_2), Z(z_1, z_2)~ bất kì. Ta có:
và
vì thế nên
Áp dụng bất đẳng thức ~|a| + |b| \geq |a+b|~ với ~(a, b) = (x_1 - y_1, y_1 - z_1)~ và ~(a, b) = (x_2 - y_2, y_2 - z_2)~, ta có:
Do ta chọn ba điểm ~X, Y, Z~ bất kì, ta có thể kết luận:
Đây là điều phải chứng minh.
Quay trở lại với định nghĩa ~V(P_i)~. Do định nghĩa vùng Voronoi sử dụng dấu ~\leq~ thay vì dấu ~<~, sẽ có trường hợp một điểm nằm trên nhiều vùng Voronoi khác nhau (điểm cách đều hai điểm trong tập ~P~). Tập hợp các điểm thuộc nhiều vùng Voronoi khác nhau của tập điểm ~P~ được gọi là sơ đồ Voronoi (Voronoi diagram) của tập điểm ~P~, kí hiệu là ~\mathcal{V}(P)~.
Sau đây là sơ đồ Voronoi sử dụng khoảng cách Euclide trong trường hợp tập ~P~ có 2 điểm và trường hợp tập ~P~ 3 điểm không thẳng hàng.
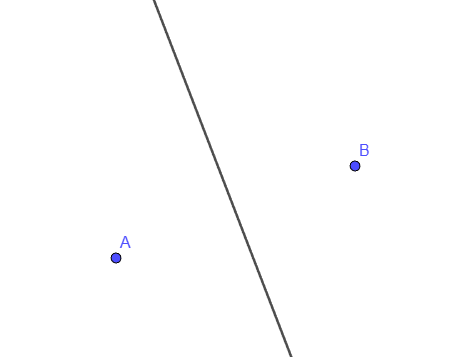
Trường hợp tập ~P~ có 2 điểm ~A~ và ~B~, sơ đồ Voronoi là đường trung trực của đoạn thẳng ~AB~.
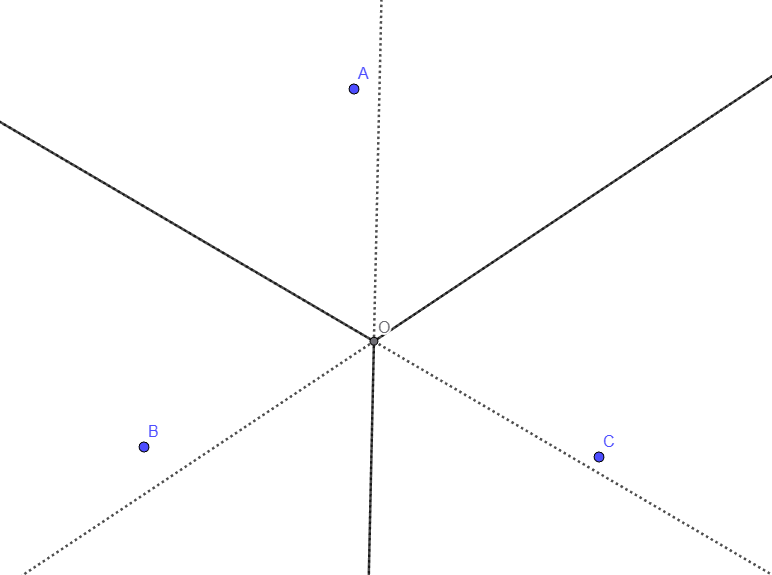
Trường hợp tập ~P~ có 3 điểm ~A~, ~B~ và ~C~ không thẳng hàng, sơ đồ Voronoi là ba tia có gốc là tâm ~O~ của đường tròn ngoại tiếp tam giác ~ABC~. Ba tia này là một phần của các đường trung trực đoạn thẳng ~AB~, ~BC~, ~CA~.
Dễ thấy bước BFS đa nguồn trong thuật toán thực chất là bước tìm vùng Voronoi cho từng điểm trong tập điểm ~P~ khi khoảng cách Manhattan được sử dụng. Ta gấp đôi tọa độ các điểm để không có điểm nguyên nào nằm trên hai vùng Voronoi khác nhau, giúp các bước sau rõ ràng và thuận tiện hơn.
Hình GIF sau minh họa quá trình tạo sơ đồ Voronoi (đường viền đậm trong hình) theo khoảng cách Manhattan bằng thuật toán BFS đa nguồn trong trường hợp ~P = \{(0, 0); (0, 10); (2, 14); (4, 18)\}~.

Lưới Delaunay
Cho tập điểm ~P = \{P_1; P_2; \dots; P_n\}~. Đồ thị ~G = (V, E)~ với ~V = P~ và ~E = \{(P_x, P_y) \mid V(P_x)~ và ~V(P_y)~ có chung một biên giới có kích thước dương~\}~ được gọi là một lưới Delaunay (Delaunay triangulation) của tập điểm ~P~, kí hiệu là ~\mathcal{D}(P)~.

Bước xây dựng tập ~E~ của thuật toán tìm cây khung Manhattan nhỏ nhất chính là bước xây dựng lưới Delaunay.
Ta thừa nhận rằng khi sử dụng khoảng cách Manhattan, ~\mathcal{D}(P)~ liên thông và là một đồ thị phẳng có ~n~ đỉnh. Do ~\mathcal{D}(P)~ là một đồ thị phẳng có ~n~ đỉnh nên nó có tối đa ~3n - 6 = \mathcal{O}(n)~ cạnh (xem định lí 5-5, trang 132 của Tài liệu giáo khoa chuyên Tin - Quyển 1).
Vấn đề cuối cùng là chứng minh tồn tại một cây khung Manhattan nhỏ nhất của tập điểm ~P~ chỉ sử dụng các cạnh của đồ thị ~\mathcal{D}(P)~.
Chứng minh
Kí hiệu ~d(X, Y)~ là khoảng cách Manhattan giữa hai điểm ~X~ và ~Y~ và đồng thời là trọng số của cạnh ~(X, Y)~ của ~\mathcal{D}(P)~ hay của một cây khung Manhattan nào đó của tập điểm ~P~.Giả sử tồn tại cây khung Manhattan nhỏ nhất của tập điểm ~P~ mà có cạnh không phải của ~\mathcal{D}(P)~. Theo nguyên lí cực hạn, trong số các cây khung như vậy, ta có thể chọn một cây khung Manhattan nhỏ nhất ~T~ của tập điểm ~P~ có ít cạnh không phải của ~\mathcal{D}(P)~ nhất. Gọi một trong những cạnh không phải của ~\mathcal{D}(P)~ đó là ~(P_x, P_y)~
Trên mặt phẳng, vẽ một đường ~S~ là đường nối điểm ~P_x~ và điểm ~P_y~ có độ dài ngắn nhất theo khoảng cách Manhattan. Đường ~S~ lần lượt đi qua các vùng Voronoi của các điểm ~P_x = V_0, V_1, V_2, ..., V_m = P_y~.
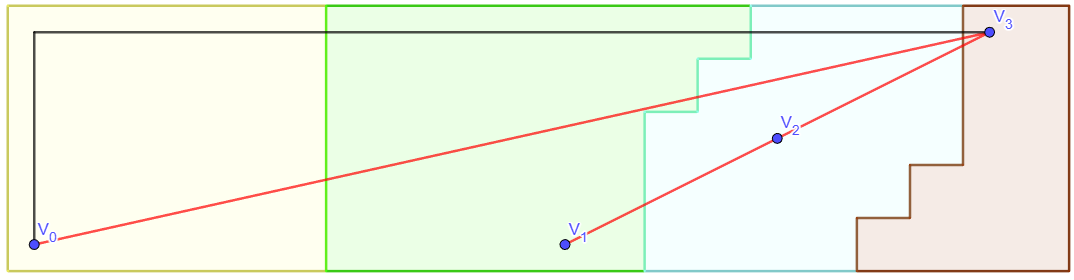
Chú ý rằng dãy các đỉnh ~V_0, V_1, V_2, \dots, V_m~ là một đường đi trên đồ thị ~\mathcal{D}(P)~.
Khi bỏ cạnh ~(P_x, P_y)~ khỏi cây khung ~T~, ta có hai cây ~T_x~ và ~T_y~ rời nhau theo thứ tự chứa đỉnh ~P_x~ và đỉnh ~P_y~. Do đó, tồn tại hai đỉnh liên tiếp ~V_i, V_{i+1}~ trên đường đi từ ~P_x~ đến ~P_y~ sao cho ~V_i~ nằm trên ~T_x~ và ~V_{i+1}~ nằm trên ~T_y~. Do ~V_i, V_{i+1}~ là hai đỉnh liên tiếp của một đường đi trên ~\mathcal{D}(P)~, dĩ nhiên ~(V_i, V_{i+1})~ là một cạnh của ~\mathcal{D}(P)~.
Ghép hai cây ~T_x~ và ~T_y~ bằng cạnh ~(V_i, V_{i+1})~, ta được một cây khung mới ~T'~.
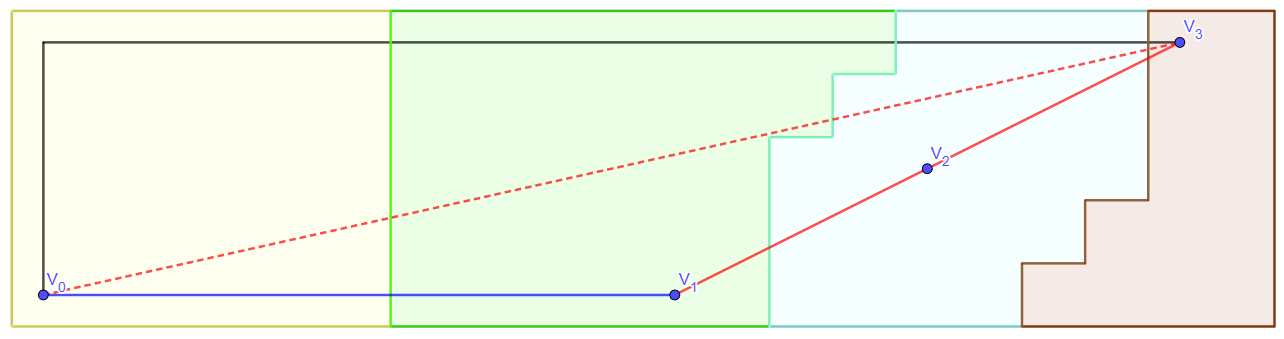
Kí hiệu ~c(X)~ là tổng trọng số các cạnh của cây khung ~X~. Ta có:
Cần chứng minh hiệu này không dương.
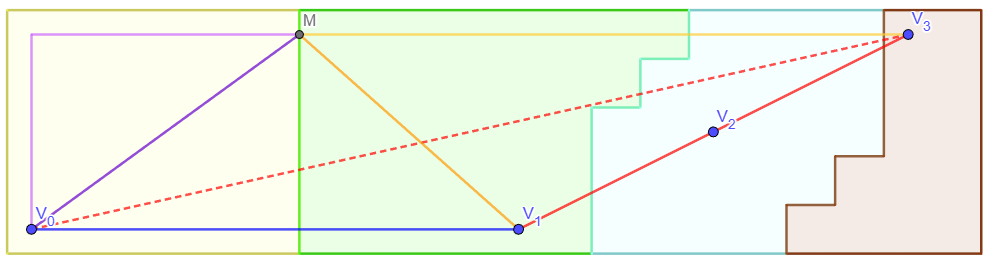
Gọi ~M~ là giao của đường ~S~ với biên giữa vùng Voronoi của ~V_i~ và vùng Voronoi của ~V_{i+1}~.
Do ~S~ là đường đi ngắn nhất từ ~P_x~ đến ~P_y~ và ~M~ nằm trên ~S~, theo tính chất của đường đi ngắn nhất, ta có:
Theo bất đẳng thức tam giác, ta có:
Do ~M~ nằm trên biên giữa vùng Voronoi của ~V_i~ và vùng Voronoi của ~V_{i+1}~, theo định nghĩa vùng Voronoi của một điểm, ta có:
và
Từ ~(1), (2), (3), (4)~, ta có:
hay
vì thế nên
Do ~T~ là một cây khung Manhattan nhỏ nhất và ~c(T') \leq c(T)~, ~T'~ phải là một cây khung Manhattan nhỏ nhất.
Tuy nhiên, do ~(P_x, P_y)~ không phải một cạnh của ~\mathcal{D}(P)~ và ~(V_i, V_{i+1})~ là một cạnh của ~\mathcal{D}(P)~, ~T'~ là một cây khung nhỏ nhất có ít cạnh không phải của ~\mathcal{D}(P)~ hơn ~T~, mâu thuẫn với việc ~T~ là cây khung nhỏ nhất có ít cạnh không phải của ~\mathcal{D}(P)~ nhất.
Vậy giả sử ban đầu sai, và ta có điều phải chứng minh.
Từ chứng minh trên, ta có thể yên tâm rằng khi thực hiện thuật toán Kruskal trên tập cạnh của ~\mathcal{D}(P)~, ta sẽ thu được một cây khung Manhattan nhỏ nhất của tập điểm ~P~.
Kết luận
Ở bài viết này, tôi đã giới thiệu một thuật toán đơn giản để tìm cây khung Manhattan nhỏ nhất cho một tập điểm có tọa độ nhỏ và chứng minh một số điểm mấu chốt liên quan đến tính đúng đắn của thuật toán này.
Do dung lượng bài viết có hạn, tôi chưa chứng minh được một số điểm (ví dụ như tính liên thông và tính phẳng của ~\mathcal{D}(P)~ khi khoảng cách Manhattan được sử dụng), xin được phép nhường những điểm đó cho bạn đọc. Ngoài ra, sau bài viết này, bạn đọc cũng có thể tìm hiểu thêm về:
- thuật toán tìm cây khung Manhattan nhỏ nhất trong ~\mathcal{O}(n \log n)~ đã được trình bày trong video chữa đề VOI 2022 của VNOI,
- các bài toán khác liên quan đến cây khung Manhattan nhỏ nhất,
- sơ đồ Voronoi và lưới Delaunay với khoảng cách Euclide và ứng dụng của chúng trong việc giải bài toán tìm cây khung Euclide nhỏ nhất.
Tham khảo
Phần sơ đồ Voronoi, lưới Delaunay và ý tưởng chứng minh trong trường hợp sử dụng khoảng cách Euclide được tham khảo trong quyển Computational Geometry in C của Joseph O'Rourke. Đây là một quyển sách kinh điển trong lĩnh vực hình học tính toán và nên được tìm hiểu bởi một thành viên của các đội thi ICPC muốn có cơ hội giải các bài hình học khó.

Bình luận