Tạp chí VNOI - Số 1: Coding Challenge #2

Coding Challenge

Coding Challenge là một chuyên mục thuộc Tạp chí VNOI, được xây dựng với mục tiêu mang đến cho cộng đồng lập trình thi đấu Việt Nam một sân chơi hữu ích và thiết thực nhằm giúp các độc giả củng cố kiến thức thuật toán và thúc đẩy tinh thần học hỏi, chia sẻ trong cộng đồng.

Hoạt động được tổ chức định kỳ hai lần mỗi tháng trên Fanpage VNOI, Group Facebook “Diễn đàn Tin học Việt Nam” và nền tảng chấm bài trực tuyến VNOJ. Toàn bộ các bài toán trong Coding Challenge được biên soạn bởi đội ngũ Tình nguyện viên thuộc Team Contest của VNOI. Chất lượng các bài toán Coding Challenge được đảm bảo về tính chuyên môn, có sự đa dạng về chủ đề và độ khó cũng như đáp ứng yêu cầu về tính chặt chẽ và chính xác.

Độc giả của Tạp chí VNOI có thể tham gia giải các bài toán thuộc Coding Challenge và gửi lời giải về cho Tạp chí. Những bài giải chất lượng sẽ được chọn lọc để đăng tải trong các số Tạp chí tiếp theo. Bên cạnh việc được ghi nhận và giới thiệu rộng rãi đến cộng đồng, các tác giả có lời giải được đăng tải sẽ nhận những phần quà tri ân từ VNOI nhằm khuyến khích tinh thần ham học hỏi và chia sẻ kiến thức đến cộng đồng

Các lời giải được chọn lọc để đăng công khai sẽ được đánh giá dựa trên tiêu chí về sự rõ ràng, mạch lạc, sáng tạo; có sự đầu tư trong diễn giải tư duy, cấu trúc và tính dễ hiểu. Đối với các bài toán có nhiều subtask, tác giả cần trình bày đầy đủ ý tưởng và hướng giải quyết cho tất cả các phần.

Phần thưởng dành cho mỗi lời giải được đăng tải trên Tạp chí là một bộ quà tặng gồm sổ tay, bút, sticker và móc khóa. Đặc biệt, với các tác giả có từ 03 bài giải trở lên được đăng trong chuyên mục, Ban biên tập Tạp chí sẽ gửi tặng một chiếc áo VNOI như lời tri ân cho những đóng góp tích cực đối với Coding Challenge.

Sau 03 số đầu tiên, Coding Challenge đã ghi nhận những kết quả rất ấn tượng. Đã có tổng cộng 2316 lượt nộp bài trên hệ thống và 26 lời giải chất lượng được gửi về cho Tạp chí. Đây là nguồn động lực to lớn để đội ngũ Tạp chí VNOI tiếp tục phát triển và mở rộng sân chơi học thuật này trong thời gian tới.

Coding Challenge #2

Coding Challenge #2 tiếp tục là một bài toán đồ thị, với chủ đề về Cây Khung Nhỏ Nhất. Điểm đặc biệt của bài toán chính là ở việc chúng ta sẽ không chỉ đi tìm một cây khung, mà cần liên tiếp thực hiện thao tác tìm kiếm để cho ra K cây khung lớn nhất (một biến thể ngược của bài toán MST nổi tiếng).

Bài toán này ghi nhận 116 độc giả tham gia giải và 28 bài giải được trọn vẹn 100/100 điểm từ bộ test. Đội ngũ Tạp chí VNOI đã chọn ra 2 lời giải cho bài toán này đến từ các độc giả của Tạp chí.

Đề Bài

Đề bài gốc có thể được đọc trên hệ thống VNOJ

Coding Challenge #2 - Đấu Thầu

Nước VNOI gồm ~n~ thành phố và đang có kế hoạch liên kết chúng bằng ~m~ con đường cao tốc hai chiều. Các con đường được đánh số từ 1 tới ~m~, con đường thứ ~i~ liên kết thành phố ~u_i~ với ~v_i~, và có lợi nhuận là ~w_i~ (các giá trị ~w_i~ phân biệt). Các con đường được thiết kế để tất cả các cặp thành phố đều có thể trực tiếp hoặc gián tiếp đi tới nhau.

Để xây dựng các con đường đó, chính quyền VNOI quyết định giao việc này cho ~k~ nhà thầu. Sau những vòng bỏ phiếu căng thẳng, các nhà thầu này được xếp ở các vị trí từ ~1~ tới ~k~ thể hiện sự ưu tiên trong việc chọn tuyến đường thi công.

Mỗi nhà thầu sẽ được chọn một tập hợp các con đường trong ~m~ đường cao tốc có sẵn trong kế hoạch, sao cho chúng không tạo ra bất kì chu trình nào và con đường không bị nhà thầu nào trước đó chọn. Giả sử, nếu nhà thầu chọn con đường ~\{1 \to 2; 2 \to 3; 3 \to 1; 4 \to 5\}~ là không thoả mãn, bởi vì có chu trình ~1 \to 2 \to 3 \to 1~. Lưu ý rằng ở ví dụ trên mũi tên được đánh hướng cho mục đích biểu diễn, còn trên thực tế thì các con đường là hai chiều.

Đầu tiên, nhà thầu thứ ~1~ sẽ được chọn trước, sau đó tới nhà thầu thứ ~2~, ... tới nhà thầu thứ ~k~. Tất nhiên với cách này, một số con đường sẽ không được xây dựng, nhưng ở giai đoạn đầu của dự án thì đây là chuyện bình thường.

Tất nhiên, mỗi nhà thầu đều muốn tối đa hoá lợi ích của mình, vậy nên khi được chọn các con đường, họ sẽ chọn tập con đường mang tới tổng lợi nhuận lớn nhất có thể.

Nhiệm vụ của bạn là tính toán trước cho chính quyền VNOI xem mỗi nhà thầu từ ~1~ tới ~k~ sẽ có lợi nhuận là bao nhiêu khi tất cả đều chọn tập con đường một cách tối ưu.

Input

Dòng đầu tiên gồm 3 số nguyên ~n, m, k~ miêu tả số thành phố, số con đường cần xây dựng và số nhà thầu;
~m~ dòng tiếp theo, dòng thứ ~i~ gồm ~3~ số nguyên ~u_i, v_i, w_i~ miêu tả con đường thứ ~i~ trong kế hoạch, kết nối thành phố ~u_i~ với ~v_i~

Output

Gồm ~k~ dòng, dòng thứ ~i~ chứa giá trị là tổng lợi nhuận của nhà thầu thứ ~i~ trong cách chia tối ưu.

Subtask

Trong tất cả các test ~w_i \le 10^9~
Có ~20~% test tương ứng ~20~% số điểm có ~n \le 10^5, m \le 5 \times 10^5; k = 1~.
Có ~25~% test tương ứng ~25~% số điểm có ~n \le 10^3, m \le 10^4; k \le 1000~.
Có ~35~% test tương ứng ~35~% số điểm có ~n \le 10^3, m \le 5 \times 10^5; k \le 10^4~.
~20~% số test còn lại tương ứng với ~20~ số điểm có ~n \le 10^5, m \le 5 \times 10^5; k \le 10^4~.

Sample

Sample 1

Input

Output

Sample 2

Input

Output

30
14
0

Tóm Tắt Đề Bài

Cho một đồ thị vô hướng liên thông ~G = (V, E)~ có ~n~ đỉnh và ~m~ cạnh mang trọng số dương.
Thực hiện thao tác sau ~k~ lần:
- Tìm tập cạnh ~E' \subseteq E~ sao cho:
  - ~E'~ không chứa chu trình;
  - ~E'~ có tổng trọng số lớn nhất có thể.
- Xóa các cạnh trong ~E'~ khỏi ~E~ (~E \leftarrow E \setminus E'~).
- Cho biết tổng trọng số của ~E'~ sau mỗi lần thực hiện thao tác.

Subtask	Điểm	Giới hạn
~1~	~20~%	~n \le 10^5, m \le 5 \times 10^5; k = 1~
~2~	~25~%	~n \le 10^3, m \le 10^4; k \le 1000~
~3~	~35~%	~n \le 10^3, m \le 5 \times 10^5; k \le 10^4~
~4~	~20~%	~n \le 10^5, m \le 5 \times 10^5; k \le 10^4~

Minh Họa Sample

Sample 1:

Minh hoạ đồ thị sau mỗi lần thực hiện thao tác

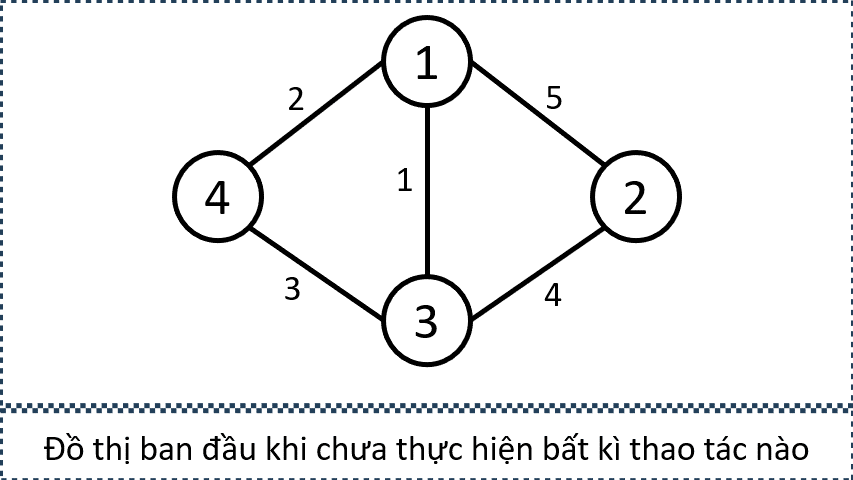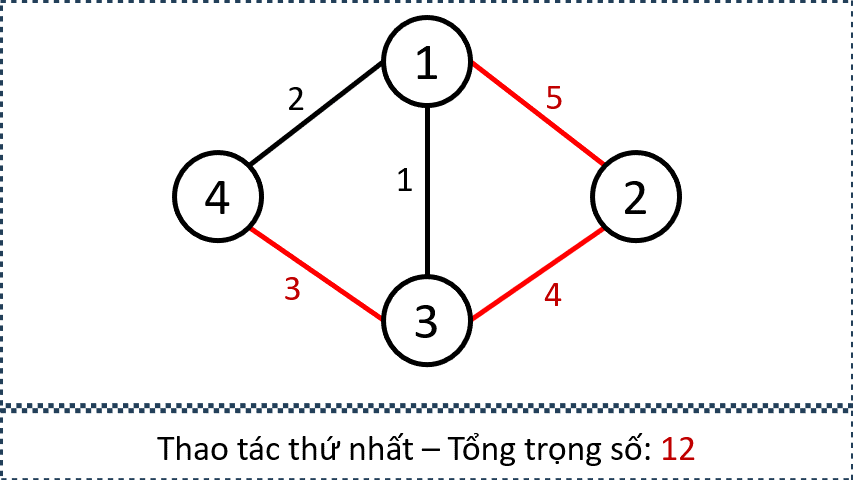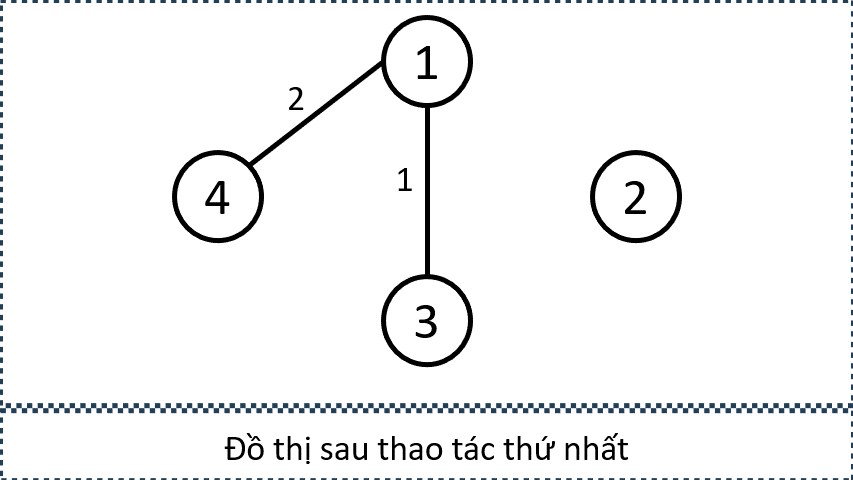
sample_01

Minh họa tập cạnh được chọn bởi các thao tác

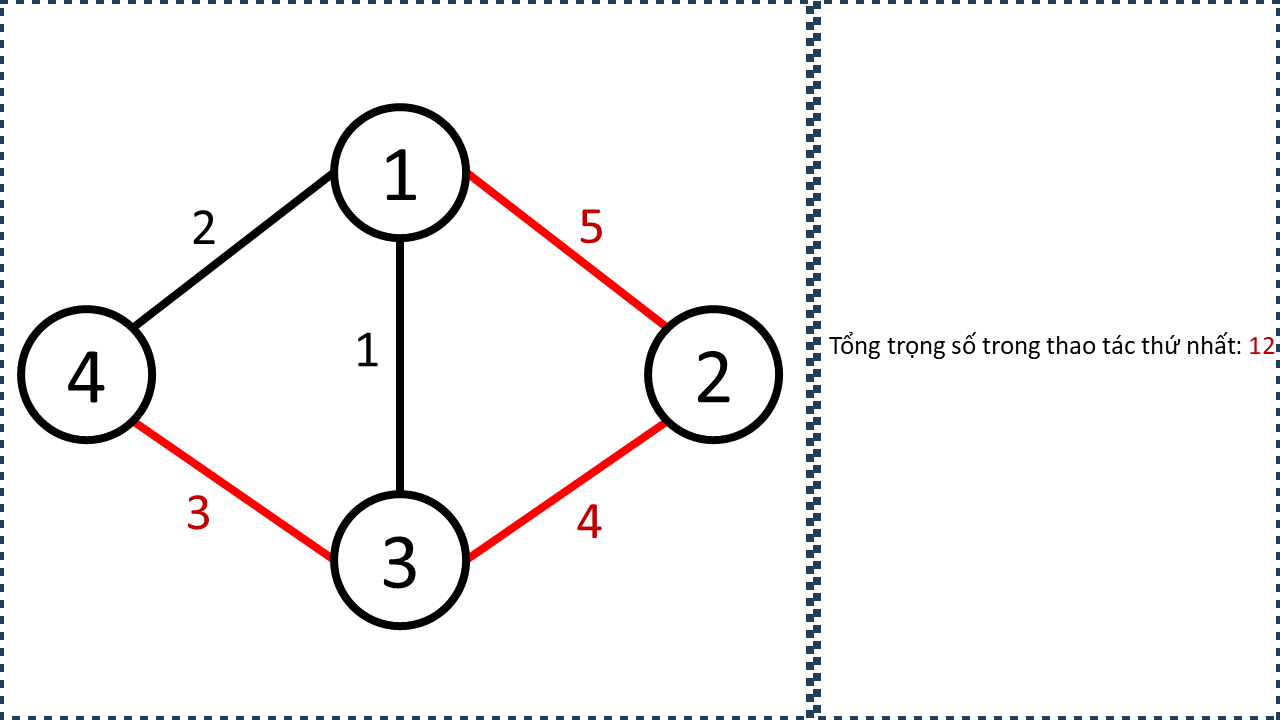
sample<em>01</em>summary

Sample 2:

Minh họa đồ thị sau mỗi lần thực hiện thao tác

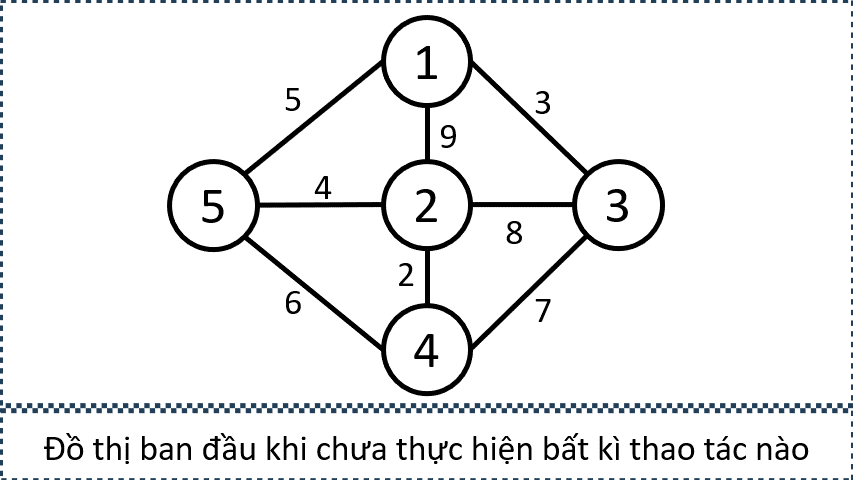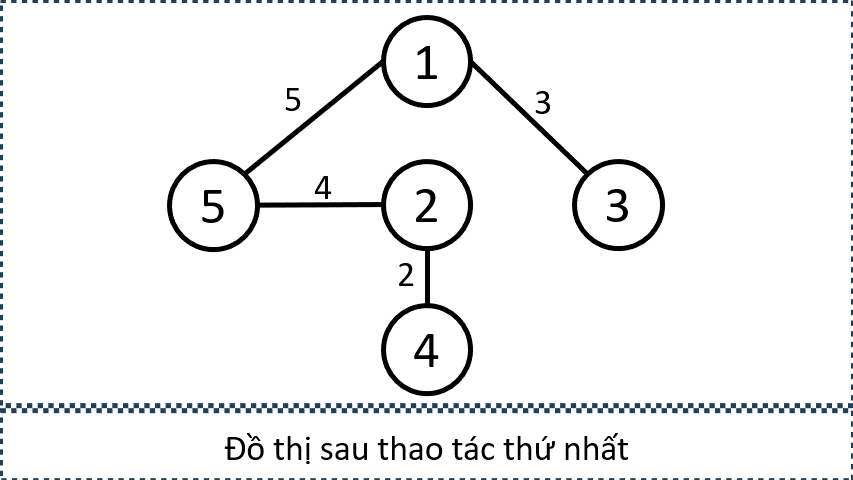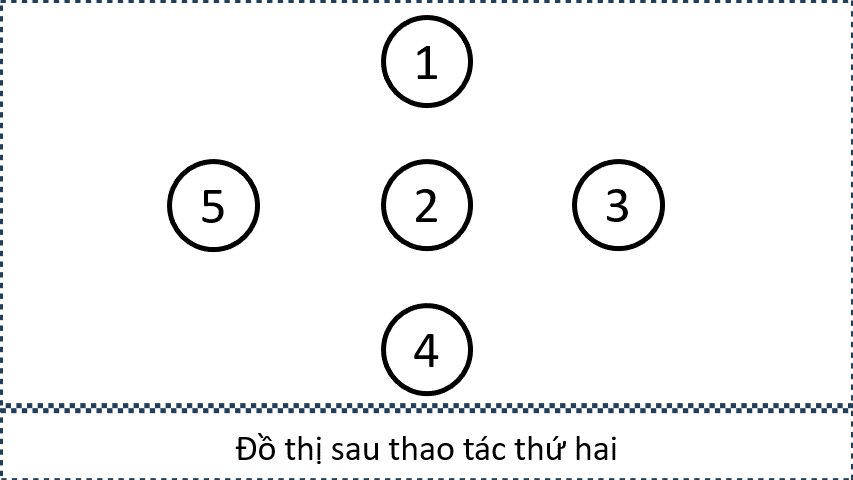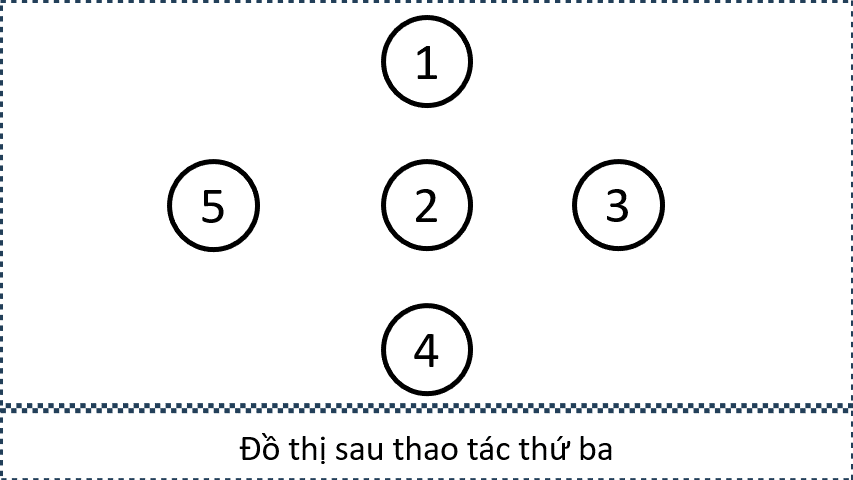
sample__02

Minh họa tập cạnh được chọn bởi các thao tác

sample<em>02</em>summary

Lời giải #1

Một số lưu ý

Đồ thị được cho trên đề bài không nhắc đến việc không tồn tại cạnh lặp.

Subtask 1: ~n\le 10^5,m\le 5\times 10^5,k=1~

Theo đề bài, các cạnh mà mỗi nhà thầu chọn không được tạo thành một chu trình. Điều này tương ứng với việc các cạnh đó phải là các cạnh của một rừng (forest).

Trong subtask 1, chỉ có duy nhất một nhà thầu nên ta có thể tóm tắt yêu cầu của subtask này như sau: Chọn ra một tập cạnh có tổng trọng số lớn nhất sao cho tập cạnh đó phải tạo thành một rừng.

Đây là dạng bài toán tìm cây khung lớn nhất trên đồ thị. Về cơ bản thì cách làm không khác gì cách làm bài toán tìm cây khung nhỏ nhất.

Về thuật toán tìm cây khung nhỏ nhất, các bạn có thể tìm hiểu tại đây.

Độ phức tạp: ~O(m\times log(m)+m\times log(n))~ (Kruskal) hoặc ~O((m+n)\times log(n))~ (Prim).

Subtask 2: ~n\le 10^3,m\le 10^4,k\le 1000~

Trong trường hợp có nhiều nhà đấu thầu hơn, rõ ràng:

Nhà đấu thầu thứ nhất sẽ chọn các cạnh để tạo thành cây khung lớn nhất (như subtask 1).
Từ nhà đấu thầu thứ hai, họ cũng sẽ chọn các cạnh để tạo thành cây khung lớn nhất từ các cạnh còn lại mà họ có thể chọn.

Như vậy, subtask này chỉ là tìm cây khung lớn nhất ~k~ lần tương ứng với ~k~ nhà đấu thầu. Với mỗi lần chọn được các cạnh cho một nhà đấu thầu, ta bỏ các cạnh đó đi để xét cạnh trên đồ thị mới cho các nhà đấu thầu sau.

Độ phức tạp: ~O(T\times k)~ với ~T~ là độ phức tạp cho mỗi lần tìm cây khung lớn nhất (subtask 1).

Subtask 3: ~n\le 10^3,m\le 5\times 10^5,k\le 10^4~

Vì giới hạn lớn nên ta không thể áp dụng cách tìm cây khung lớn nhất như cách làm của subtask 1/2.

Dựa trên thuật toán Kruskal, ta có một cách làm khác để giải subtask 2 như sau:

Ta tạo ~k~ cây khung tương ứng với ~k~ nhà đấu thầu. Sắp xếp lại các cạnh theo trọng số giảm dần.
Khi xét từng cạnh, nếu cạnh đó có thể thêm vào cây khung thứ nhất thì ta sẽ thêm. Trong trường hợp ngược lại, ta sẽ xét cây khung thứ hai, và cứ vậy đến cây khung thứ ~k~ (chọn cây khung có chỉ số nhỏ nhất mà ta có thể thêm cạnh).
Cách duyệt này vẫn đảm bảo việc chọn ra được cây khung lớn nhất cho tất cả ~k~ nhà đấu thầu.

Tới đây ta có một nhận xét:

Gọi ~f(i,j,p)~ là hàm kiểm tra tính liên thông của cặp đỉnh ~(i,j)~ trên cây khung thứ ~p~. ~f(i,j,p)=1~ khi hai đỉnh này cùng nằm trên một TPLT của cây khung thứ ~p~ và ~f(i,j,p)=0~ trong trường hợp ngược lại.
Khi đó, ~f(i,j,p)\ge f(i,j,p+1)\forall 1\le i,j\le n,1\le p<k~.</li>
Nói cách khác, tính liên thông của mọi cặp đỉnh ~(i,j)~ giảm dần theo chỉ số ~p~ của cây khung.

Với tính chất của hàm ~f(i,j,p)~, ta có thể thực hiện tìm kiếm nhị phân để tìm cây khung có chỉ số nhỏ nhất mà ~f(i,j,p)=0~ mỗi khi xét cạnh ~(i,j)~.

Độ phức tạp cho mỗi lần xét cạnh sẽ là ~O(log(n)\times log(k))~ hoặc có thể nhỏ hơn nếu thực hiện tối ưu như nén đường đi hay gộp theo kích cỡ.

Độ phức tạp: ~O(m\times log(n)\times log(k))~.

Subtask 4: ~n\le 10^5,m\le 5\times 10^5,k\le 10^4~

Việc dựng ~k~ cây khung một cách thủ công sẽ không thể thực hiện như subtask 3 vì ~n\times k\le 10^9~, giới hạn này là rất lớn để có thể lưu trữ.

Trên thực tế, ta không cần phải lưu hết trạng thái của các đỉnh vì nếu có đỉnh không phải là một trong hai đầu của bất kỳ cạnh nào của cây khung thì không cần phải lưu trữ. Vì thế nên ta có thể sử dụng std::map hoặc cây tiền tố (trie) để lưu tất cả những nút cần lưu trữ thông tin. Điều này giúp việc thực hiện các thao tác trên DSU cũng chỉ mất ~O(log(n))~.

Lưu ý: Cần phải cài đặt cẩn thận vì có thể sẽ bị TLE (time limit exceed).

Độ phức tạp: ~O(m\times log(n)\times log(k))~.

Lời giải #2

Subtask 1: Giới hạn: ~n \le 10^5, m \le 5 \times 10^5; k = 1~

Ý Tưởng:

Vì số thao tác cần phải thực hiện ~k~ là ~1~, bài toán có thể được quy về tìm cây khung lớn nhất (ngược với bài toán tìm cây khung nhỏ nhất) trong đồ thị đã cho bởi:
- Vì tập cạnh được chọn, tạm gọi là ~E'~, không được chứa chu trình, ~E'~ phải là một rừng.
- Hơn nữa, vì đồ thị ban đầu liên thông, để tổng trọng số là lớn nhất, ~E'~ phải là một cây khung (rừng liên thông gồm ~n - 1~ cạnh). Nếu ~E'~ không liên thông, ta có thể thêm một cạnh mới mà không tạo ra chu trình, làm tăng tổng trọng số. Điều này mâu thuẫn với giả thiết tối ưu.
Để tìm cây khung lớn nhất, ta có thể sử dụng thuật toán Kruskal với một thay đổi nhỏ: Thay vì sắp xếp các cạnh theo thứ tự tăng dần trọng số, ta sắp xếp giảm dần.

Cách chứng minh thứ nhất (ngắn gọn):

Bài toán tìm cây khung lớn nhất trên đồ thị ~G = (V, E)~ có thể được quy về bài toán tìm cây khung nhỏ nhất trên đồ thị ~G' = (V, E)~ với cùng tập đỉnh và cạnh, nhưng với trọng số mới được đảo dấu (~w'_e = -w_e~ cho mọi cạnh ~e \in E~). Khi đó, cây khung nhỏ nhất của ~G'~ cũng chính là cây khung lớn nhất của ~G~.
Thuật toán Kruskal có thể được dùng để tìm cây khung nhỏ nhất với các cạnh được duyệt theo thứ tự trọng số tăng dần. Khi áp dụng thuật toán trên đồ thị ~G'~, thứ tự này tương đương với việc duyệt các cạnh của ~G~ theo thứ tự trọng số giảm dần.

Cách chứng minh thứ hai (chi tiết):

Lưu ý: Cách chứng minh này phần lớn giống với cách minh tính đúng đắn của thuật toán Kruskal.

Ta có thể chứng minh tính đúng đắn của ý tưởng trên bằng cách chứng minh quy nạp theo số lượng cạnh đã chọn với mệnh đề sau: "Với tập cạnh ~M~ được chọn bởi thuật toán tại mọi thời điểm, đồ thị luôn chứa một cây khung lớn nhất với tập cạnh ~T~ chứa mọi cạnh của ~M~".
- Trường hợp cơ sở: Mệnh đề trên hiển nhiên đúng với trường hợp ban đầu, khi ~M~ không chứa bất kì cạnh nào bởi tập rỗng luôn là tập con của bất kì cây khung lớn nhất nào.
- Bước quy nạp: Khi ta xem xét có nên thêm cạnh ~e~ vào ~M~ đang thỏa mệnh đề trên không, ta có ba trường hợp sau:
1. ~M \cup \{e\}~ chứa chu trình (thêm cạnh ~e~ vào ~M~ tạo nên một chu trình): Thuật toán sẽ không thêm ~e~ vào ~M~. Vì vậy, mệnh đề sẽ vẫn thỏa bởi ~T~ cũng không thể chứa ~e~ (~T~ là một cây khung nên không chứa chu trình).
2. ~T~ chứa ~e~: Mệnh đề trên tiếp tục thỏa.
3. ~T~ không chứa ~e~: Khi thêm cạnh ~e~ vào ~T~, ta có ~T \cup {e}~ chứa một chu trình duy nhất có chứa cạnh ~e~. Chu trình này phải chứa ít nhất một cạnh ~f~ không ở trong ~M~. Nếu không, việc thêm ~e~ vào ~M~ đã tạo chu trình, tức rơi vào trường hợp đầu tiên.
Vì cạnh ~f~ đã không được chọn bởi thuật toán trước đó, trọng số của cạnh ~f~ không thể lớn hơn trọng số cạnh ~e~ (~w_f \leq w_e~). Khi này, ta nhận thấy rằng cây khung với tập cạnh ~T' = T \cup \{e\} \setminus \{f\}~ cũng là cây khung lớn nhất bởi tổng trọng số của ~T'~ không nhỏ hơn tổng trọng số của ~T~. Mệnh đề vì thế vẫn tiếp tục được thỏa bởi ~M \cup \{e\}~ là tập con của tập cạnh ~T'~ của một cây khung lớn nhất.

Độ Phức Tạp:

Ý tưởng trên có thể được cài đặt với độ phức tạp thời gian ~O(m \log m + n)~ bằng cách sử dụng cấu trúc dữ liệu Disjoint Set Union để quản lý các thành phần liên thông như trong bài toán tìm cây khung nhỏ nhất.

Giải thích:

Bước khởi tạo cấu trúc dữ liệu Disjoint Set Union có thể có độ phức tạp ~O(n)~.
Bước sắp xếp cạnh có độ phức tạp ~O(m \log m)~.
Với mỗi lần xem xét một cạnh ~e = (u, v)~, ta cần kiểm tra hai đỉnh của cạnh ~e~ có cùng thuộc một thành phần liên thông không và nếu không thuộc thì ta có gộp hai thành phần liên thông chứa ~u~ và ~v~ lại. Nếu ta cài đặt cấu trúc dữ liệu Disjoint Set Union với cả hai phương pháp gộp theo kính cỡ và nén đường đi, một lần xem xét thêm cạnh như trên có độ phức tạp ~O(\alpha(n))~ với ~\alpha~ là hàm Ackermann nghịch đảo.

Vì ta duyệt ~m~ cạnh, bước xém xét hết tất cả các cạnh sẽ có độ phức tạp ~O(m \cdot \alpha(n))~.

Độ phức tạp tổng lúc này sẽ là ~O(m \log m) + O(m \cdot \alpha(n)) + O(n) = O(m \log m + n)~.

Lưu ý: Nếu ta chỉ dùng một trong phương pháp nêu trên khi cài đặt cấu trúc dữ liệu Disjoint Set Union, một lần xem xét thêm cạnh như trên có độ phức tạp ~O(\log(n))~. Khi này, độ phức tạp tổng sẽ là ~O(m \cdot (\log(m) + \log(n)) + n)~.

Với cách cài đặt này, độ phức tạp bộ nhớ là ~O(n + m)~.

Giải thích:

Lưu danh sách cạnh chiếm cần ~O(m)~ bộ nhớ.
Cấu trúc dữ liệu Disjoint Set Union cần ~O(n)~ bộ nhớ.

Code Minh Họa:

#include <bits/stdc++.h>
using namespace std;

class DisjointSetUnion {
private:

    mutable vector<int> roots;

public:

    DisjointSetUnion() {};

    DisjointSetUnion(const int n): roots(n, -1) {};

    int getRoot(const int x) const {
        return (roots[x] < 0) ? x : (roots[x] = getRoot(roots[x]));
    }

    bool checkConnected(const int x, const int y) const {
        return getRoot(x) == getRoot(y);
    }

    bool unite(int x, int y) {
        x = getRoot(x);
        y = getRoot(y);
        if (x == y)
            return false;
        if (roots[x] > roots[y])
            swap(x, y);
        roots[x] += roots[y];
        roots[y] = x;
        return true;
    }

};

constexpr int MAX_N = 1E5 + 5, MAX_M = 1E5 + 5, MAX_K = 1E4 + 4;

int n, m, k;
vector<tuple<int, int, int> > edges;

void input() {
    cin >> n >> m >> k;

    edges.resize(m);

    for (auto &[w, u, v] : edges)
        cin >> u >> v >> w;
}

void solve() {
    DisjointSetUnion dsu(n + 1);
    long long result = 0;

    sort(edges.rbegin(), edges.rend());

    for (const auto &[w, u, v] : edges)
        if (dsu.unite(u, v))
            result += w;

    cout << result << '\n';
}

signed main() {
    #ifdef LOCAL
    freopen("input.INP", "r", stdin);
    #endif // LOCAL

    cin.tie(0) -> sync_with_stdio(0);
    cout.tie(0);

    input();
    solve();

    return 0;
}

Subtask 2: Giới hạn: ~n \le 10^3, m \le 10^4; k \le 1000~

Ý Tưởng:

Giới hạn của Subtask 2 cho phép chúng ta thực hiện ý tưởng đề cập trong Subtask 1 ~k~ lần mà vẫn đảm bảo được độ phức tạp thời gian cho phép. Cụ thể hơn, với mỗi thao tác, ta có thể thực hiện lại ý tưởng trong Subtask 1 rồi xóa tập cạnh được chọn bởi thao tác khỏi đồ thị để ta có thể xử lý các thao tác sau. >[!Note] Lưu ý: >Vì sau khi xóa cạnh khỏi đồ thị, đồ thị có thể không liên thông nữa, tập cạnh mà chúng ta cần tìm lúc này có thể là một rừng thay vì chỉ một cây khung: với mỗi thành phần liên thông trong đồ thị hiện tại, ta cần tìm cây khung lớn nhất trong thành phần liên thông đó; tập cạnh chúng ta cần tìm sẽ là tập cạnh được tạo bởi các cạnh của các khung đó.

Độ Phức Tạp:

Ý tưởng trên có thể được cài đặt với độ phức tạp ~O(m \log m + k \cdot (n + m \cdot \alpha(n)))~.
Độ phức tạp bộ nhớ sẽ tương tự như trong Subtask 1, tức ~O(n + m)~.

Code Minh Họa:

#include <bits/stdc++.h>
using namespace std;

class DisjointSetUnion {
private:

    mutable vector<int> roots;

public:

    DisjointSetUnion(const int n): roots(n, -1) {};

    void reload() {
        fill(roots.begin(), roots.end(), -1);
    }

    int getRoot(const int x) const {
        return (roots[x] < 0) ? x : (roots[x] = getRoot(roots[x]));
    }

    bool checkConnected(const int x, const int y) const {
        return getRoot(x) == getRoot(y);
    }

    bool unite(int x, int y) {
        x = getRoot(x);
        y = getRoot(y);
        if (x == y)
            return false;
        if (roots[x] > roots[y])
            swap(x, y);
        roots[x] += roots[y];
        roots[y] = x;
        return true;
    }

};

constexpr int MAX_N = 1E5 + 5, MAX_M = 1E5 + 5, MAX_K = 1E4 + 4;

int n, m, k;
vector<tuple<int, int, int> > edges;

void input() {
    cin >> n >> m >> k;

    edges.resize(m);

    for (auto &[w, u, v] : edges)
        cin >> u >> v >> w;
}

void solve() {
    DisjointSetUnion dsu(n + 1);
    vector<bool> removed(m);
    long long result = 0;

    sort(edges.rbegin(), edges.rend());

    for (int t = 0; t < k; ++t) {
        result = 0;
        dsu.reload();

        for (int i = 0; i < m; ++i) {
            if (removed[i])
                continue;
            const auto &[w, u, v] = edges[i];
            if (dsu.unite(u, v)) {
                removed[i] = true;
                result += w;
            }
        }

        cout << result << '\n';
    }
}

signed main() {
    #ifdef LOCAL
    freopen("input.INP", "r", stdin);
    #endif // LOCAL

    cin.tie(0) -> sync_with_stdio(0);
    cout.tie(0);

    input();
    solve();

    return 0;
}

Subtask 3: Giới hạn: ~n \le 10^3, m \le 5 \times 10^5; k \le 10^4~

Ý Tưởng:

Đặt ~S_{i, j}~ (với ~1 \leq i \leq k~ và ~0 \leq j \leq m~) là tập cạnh được chọn trong thao tác thứ ~i~ sau khi đã xét ~j~ cạnh trong danh sách các cạnh được sắp xếp theo trọng số giảm dần. Chi tiết và ví dụ:

Lưu ý: Phần này trình bày chi tiết cách xác định tập cạnh ~S_{i, j}~ theo định nghĩa trên. Nội dung này có thể không bắt buộc phải đọc để hiểu ý tưởng chính, mà chỉ nhằm làm rõ hơn định nghĩa ~S_{i, j}~.

Chi Tiết
- Với ~j = 0~, ta có ~S_{i,j} = \emptyset~ vì chưa có cạnh nào được xét ở thời điểm bắt đầu thao tác thứ ~i~.
- Với ~1 \leq j \leq m~, đặt ~e~ là cạnh thứ ~j~. Khi đó, ta có thể xác định ~S_{i, j}~ như sau:
  - ~S_{i, j} = S_{i, j - 1}~ nếu một trong hai điều kiện sau thỏa:
    - Cạnh ~e~ đã được chọn trước đó: ~\exists z ((1 \leq z < i) \land (e \in S_{z,j}))~
    - Việc thêm cạnh ~e~ sẽ tạo thành một chu trình trong tập hiện tại: ~S_{i, j - 1} \cup \{e\}~ chứa ít nhất một chu trình.
  - ~S_{i, j} = S_{i, j - 1} \cup \{e\}~ trong trường hợp còn lại.
Ví dụ
- Với test ví dụ thứ hai, các cạnh sau khi được sắp xếp giảm dần theo trọng số có thứ tự như sau:
  
  ~ \begin{array}{|c|*{8}{c|}} \hline \textbf{i} & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ \hline e_i & (1,2) & (2,3) & (3,4) & (4,5) & (1,5) & (2,5) & (1,3) & (2,4) \\ \hline w_i & 9 & 8 & 7 & 6 & 5 & 4 & 3 & 2 \\ \hline \end{array} ~
- Giá trị ~S_{i, j}~ được tính như bảng sau:
  
  ~ \begin{array}{|c|*{3}{l|}} \hline \textbf{ j\i } & \textbf{1} & \textbf{2} & \textbf{3} \\ \hline 0 & \emptyset & \emptyset & \emptyset \\ \hline 1 & \{(1,2)\} & \emptyset & \emptyset \\ \hline 2 & \{(1,2), (2,3)\} & \emptyset & \emptyset \\ \hline 3 & \{(1,2), (2,3), (3,4)\} & \emptyset & \emptyset \\ \hline 4 & \{(1,2), (2,3), (3,4), (4,5)\} & \emptyset & \emptyset \\ \hline 5 & \{(1,2), (2,3), (3,4), (4,5)\} & \{(1, 5)\} & \emptyset \\ \hline 6 & \{(1,2), (2,3), (3,4), (4,5)\} & \{(1, 5), (2, 5)\} & \emptyset \\ \hline 7 & \{(1,2), (2,3), (3,4), (4,5)\} & \{(1, 5), (2, 5), (1, 3)\} & \emptyset \\ \hline 8 & \{(1,2), (2,3), (3,4), (4,5)\} & \{(1, 5), (2, 5), (1, 3), (2, 4)\} & \emptyset \\ \hline \end{array} ~
Ta nhận thấy rằng nếu cạnh thứ ~j~, gọi là ~e_j~, được chọn trong bất kì một thao tác ~i~ nào thì ~i~ chính là giá trị nhỏ nhất sao cho với mọi thao tác ~z~ trước ~i~ (~1 \leq z < i~), việc thêm ~e_j~ vào ~S_{z, j - 1}~ sẽ tạo thành chu trình. Nếu không, cạnh ~e_j~ đã nên được chọn trước thao tác ~i~. Ta có: ~i = \min\{x \mid \forall z ((1 \leq z < x) \rightarrow C(S_{z, j - 1} \cup \{e_j\})) \}~ với ~C~ là mệnh đề "đồ thị con tạo bởi tập cạnh ~A~ chứa ít nhất một chu trình".
Dựa vào nhận xét trên, ta có thể duyệt qua từng cạnh và dùng kỹ thuật chặt nhị phân để xác định thao tác sớm nhất có thể chứa cạnh đó mà không tạo chu trình. Để kiểm tra việc một chu trình có thể xuất hiện hay không khi thêm một cạnh nào đó, với mỗi thao tác, ta sử dụng một cấu trúc dữ liệu để quản lý thành phần liên thông trong suốt quá trình duyệt qua các cạnh. Ý tưởng cài đặt: Ta có thể sử dụng ~k~ cấu trúc dữ liệu Disjoint Set Union để quản lý thành phần liên thông giữa ~n~ đỉnh cho ~k~ thao tác.

Độ Phức Tạp:

Ý tưởng trên có thể được cài đặt với độ phức tạp ~O(m \log m + k \cdot n + m \log k \cdot \alpha(n))~.

Giải thích:
- Bước sắp xếp cạnh có độ phức tạp ~O(m \log m)~ (tương tự như trong Subtask 1).
- Việc khởi tạo ~k~ cấu trúc dữ liệu Disjoint Set Union để quản lý thành phần liên thông trên ~n~ đỉnh có độ phức tạp ~O(k \cdot n)~.
- Bước xử lý các cạnh có độ phức tạp ~O(m \log k \cdot \alpha(n))~.
  - Với mỗi lần xét cạnh, chúng ta tìm được thao tác (nếu tồn tại) mà chứa được cạnh đang xét sau tối đa ~O(\log k)~ bước chặt nhị phân.
  - Với mỗi lần chặt nhị phân, việc kiểm tra việc hai đỉnh của cạnh đang xét có đang thuộc cùng một thành phần liên thông có độ phức tạp ~O(\alpha(n))~ (tương tự như trong Subtask 1).
  - Chúng ta phải xét qua ~O(m)~ cạnh.
  - Ngoài ra, chúng ta có thể phải cập nhật thành phần liên thông cuối mỗi lần xét cạnh với độ phức tạp ~O(\alpha(n))~.

Độ phức tạp tổng vì thế là ~O(m \cdot (\log k \cdot \alpha(n) + \alpha(n))) = O(m \log k \cdot \alpha(n))~

Với cách cài đặt này, độ phức tạp bộ nhớ là ~O(m + k \cdot n)~. Giải thích:
- Lưu danh sách cạnh chiếm cần ~O(m)~ bộ nhớ (tương tự như trong Subtask 1).
- Lưu ~k~ cấu trúc dữ liệu Disjoint Set Union cần ~O(k \cdot n)~ bộ nhớ.

Code Minh Họa:

#include <bits/stdc++.h>
using namespace std;

class DisjointSetUnion {
private:

    mutable vector<int> roots;

public:

    DisjointSetUnion() {};

    DisjointSetUnion(const int n): roots(n, -1) {};

    int getRoot(const int x) const {
        return (roots[x] < 0) ? x : (roots[x] = getRoot(roots[x]));
    }

    bool checkConnected(const int x, const int y) const {
        return getRoot(x) == getRoot(y);
    }

    bool unite(int x, int y) {
        x = getRoot(x);
        y = getRoot(y);
        if (x == y)
            return false;
        if (roots[x] > roots[y])
            swap(x, y);
        roots[x] += roots[y];
        roots[y] = x;
        return true;
    }

};

constexpr int MAX_N = 1E5 + 5, MAX_M = 1E5 + 5, MAX_K = 1E4 + 4;

int n, m, k;
long long result[MAX_K];
vector<DisjointSetUnion> graphs;
vector<tuple<int, int, int> > edges;

void input() {
    cin >> n >> m >> k;

    edges.resize(m);

    for (auto &[w, u, v] : edges)
        cin >> u >> v >> w;
}

void solve() {
    int low = 0, middle = 0, high = 0;

    graphs.resize(k + 1, DisjointSetUnion(n + 1));

    sort(edges.rbegin(), edges.rend());

    for (const auto &[w, u, v] : edges) {
        low = 0;
        high = k + 1;
        while (low + 1 < high) {
            middle = low + high >> 1;
            if (graphs[middle].checkConnected(u, v))
                low = middle;
            else
                high = middle;
        }
        if (high <= k) {
            graphs[high].unite(u, v);
            result[high] += w;
        }
    }

    for (int i = 1; i <= k; ++i)
        cout << result[i] << '\n';
}

signed main() {
    #ifdef LOCAL
    freopen("input.INP", "r", stdin);
    #endif // LOCAL

    cin.tie(0) -> sync_with_stdio(0);
    cout.tie(0);

    input();
    solve();

    return 0;
}

Subtask 4: Giới hạn: ~n \le 10^5, m \le 5 \times 10^5; k \le 10^4~

Ý Tưởng:

Lưu ý: Ý tưởng chính sử dụng trong Subtask này cũng giống như trong Subtask 3. Điểm khác biệt chính nằm ở hướng cài đặt ý tưởng.

Nhận xét về độ phức tạp của cách cài đặt cho Subtask 3: Với độ phức tạp của cách cài đặt cho Subtask 3, ta nhận thấy rằng việc quản lý các thành phần liên thông cho từng thao tác, là phần có chi phí tính toán nặng trong trường hợp tệ nhất (với độ phức tạp ~O(k \cdot n)~). Mặt khác, các bước xử lý còn lại có chi phí tính toán chấp nhận được. Vì vậy, nếu ta muốn cải thiện ý tưởng đó, ta cần phải tối ưu những bước xử lý liên quan tới quản lý thành phần liên thông.
Ta có một số nhận xét như sau:
- Với cách cài đặt đề cập trong Subtask 3, ta cần phải quan lý tổng cộng ~k \cdot n~ đỉnh (mỗi cấu trúc dữ liệu Disjoint Set Union quản lý ~n~ đỉnh). Tuy nhiên, trong suốt quá trình xử lý ~m~ cạnh, chỉ có tối đa ~2 \cdot m~ đỉnh thuộc các thành phần liên thông có kích thước lớn hơn ~1~. Giải thích: Mỗi cạnh được xét nếu được thêm vào chỉ có thể làm tăng số lượng đỉnh nằm trong một thành phần liên thông không đơn lẻ thêm tối đa ~2~ đỉnh.
- Khi kiểm tra hai đỉnh ~u~ và ~v~ khác nhau có thuộc cùng một thành phần liên thông hay không, ta nhận thấy rằng: nếu một trong hai đỉnh thuộc một thành phần có kích thước bằng ~1~ thì ~u~ và ~v~ chắc chắn không cùng thành phần liên thông. ~\Rightarrow~ Dựa trên những nhận xét trên, ta chỉ cần quản lý các thành phần liên thông có kích thước ít nhất là ~2~ đỉnh, và xử lý riêng các trường hợp thành phần liên thông chỉ có một đỉnh. Về mặt cài đặt, ta chỉ cần thêm đỉnh vào cấu trúc dữ liệu Disjoint Set Union khi ta cần gộp thành phần liên thông của đỉnh đó với đỉnh khác.

Độ Phức Tạp

Ý tưởng trên có thể được cài đặt với độ phức tạp ~O(m \log m + k + m \log k \cdot \alpha(n))~. Giải thích:
- Việc quản lý các thành phần liên thông giờ đây chỉ có độ phức tạp ~O(k)~ để khởi tạo và ~O(m)~ để thêm đỉnh khi xử lý tất cả ~m~ cạnh. Vì thế độ phức tạp tổng của cách cài đặt là ~O(m \log m) + O(k) + O(m) + O(m \log k \cdot \alpha(n)) = O(m \log m + k + m \log k \cdot \alpha(n))~
Với cách cài đặt này, độ phức tạp bộ nhớ là ~O(m + k)~. Giải thích:
- Lưu danh sách cạnh chiếm cần ~O(m)~ bộ nhớ như trong Subtask 1.
- Lưu ~k~ cấu trúc dữ liệu Disjoint Set Union cần ~O(k)~ bộ nhớ và cần thêm ~O(m)~ bộ nhớ do chúng ta có thể thêm tối đa ~2 \cdot m~ đỉnh. ~\Rightarrow~ Độ phức tạp tổng của cách cài đặt là ~O(m) + O(m) + O(k) = O(m + k)~.

Code Minh Họa:

#include <bits/stdc++.h>
using namespace std;

class DisjointSetUnion {
private:

    mutable vector<int> roots;

public:

    DisjointSetUnion() {};

    int getRoot(const int x) const {
        return (roots[x] < 0) ? x : (roots[x] = getRoot(roots[x]));
    }

    bool checkConnected(const int x, const int y) const {
        return getRoot(x) == getRoot(y);
    }

    int addVertex() {
        const int result = roots.size();
        roots.push_back(-1);
        return result;
    }

    bool unite(int x, int y) {
        x = getRoot(x);
        y = getRoot(y);
        if (x == y)
            return false;
        if (roots[x] > roots[y])
            swap(x, y);
        roots[x] += roots[y];
        roots[y] = x;
        return true;
    }

};

class UndirectedGraph {
private:

    unordered_map<int, int> ids;
    DisjointSetUnion dsu;

public:

    bool checkConnected(const int x, const int y) const {
        const auto a = ids.find(x);
        if (a == ids.end())
            return false;
        const auto b = ids.find(y);
        if (b == ids.end())
            return false;
        return dsu.checkConnected(a -> second, b -> second);
    }

    int getID(const int x) {
        const auto a = ids.find(x);
        if (a == ids.end())
            return ids[x] = dsu.addVertex();
        return a -> second;
    }

    bool unite(const int x, const int y) {
        return dsu.unite(getID(x), getID(y));
    }

};

constexpr int MAX_N = 1E5 + 5, MAX_M = 1E5 + 5, MAX_K = 1E4 + 4;

int n, m, k;
long long result[MAX_K];
vector<UndirectedGraph> graphs;
vector<tuple<int, int, int> > edges;

void input() {
    cin >> n >> m >> k;

    edges.resize(m);

    for (auto &[w, u, v] : edges)
        cin >> u >> v >> w;
}

void solve() {
    int low = 0, middle = 0, high = 0;

    graphs.resize(k + 1);

    sort(edges.rbegin(), edges.rend());

    for (const auto &[w, u, v] : edges) {
        low = 0;
        high = k + 1;
        while (low + 1 < high) {
            middle = low + high >> 1;
            if (graphs[middle].checkConnected(u, v))
                low = middle;
            else
                high = middle;
        }
        if (high <= k) {
            graphs[high].unite(u, v);
            result[high] += w;
        }
    }

    for (int i = 1; i <= k; ++i)
        cout << result[i] << '\n';
}

signed main() {
    #ifdef LOCAL
    freopen("input.INP", "r", stdin);
    #endif // LOCAL

    cin.tie(0) -> sync_with_stdio(0);
    cout.tie(0);

    input();
    solve();

    return 0;
}

Coding Challenge

Coding Challenge #2

Đề Bài

Coding Challenge #2 - Đấu Thầu

Input

Output

Subtask

Sample

Sample 1

Input

Output

Sample 2

Input

Output

Tóm Tắt Đề Bài

Minh Họa Sample

Sample 1:

Sample 2:

Lời giải #1

Một số lưu ý

Subtask 1: ~n\le 10^5,m\le 5\times 10^5,k=1~

Subtask 2: ~n\le 10^3,m\le 10^4,k\le 1000~

Subtask 3: ~n\le 10^3,m\le 5\times 10^5,k\le 10^4~

Subtask 4: ~n\le 10^5,m\le 5\times 10^5,k\le 10^4~

Lời giải #2

Subtask 1: Giới hạn: ~n \le 10^5, m \le 5 \times 10^5; k = 1~

Ý Tưởng:

Cách chứng minh thứ nhất (ngắn gọn):

Cách chứng minh thứ hai (chi tiết):

Độ Phức Tạp:

Code Minh Họa:

Subtask 2: Giới hạn: ~n \le 10^3, m \le 10^4; k \le 1000~

Ý Tưởng:

Độ Phức Tạp:

Code Minh Họa:

Subtask 3: Giới hạn: ~n \le 10^3, m \le 5 \times 10^5; k \le 10^4~

Ý Tưởng:

Độ Phức Tạp:

Giải thích:

Code Minh Họa:

Subtask 4: Giới hạn: ~n \le 10^5, m \le 5 \times 10^5; k \le 10^4~

Ý Tưởng:

Độ Phức Tạp

Code Minh Họa:

Bình luận