Viettel Programming Challenge 2023
Điểm: 100
Kì thi Viettel Programming Challenge 2023 được tổ chức với địa điểm thi ngay tại hội trường trung tâm. Theo thể lệ, các đội tham dự cuộc thi đều phải có đúng ba thành viên. Ngoài các đội thi chính thức thì kì thi còn có sự góp mặt tham gia của một đội thi khách mời đặc biệt cũng gồm ba thành viên. Tuy nhiên, do sự cố tắc đường mà đội thi khách mời đã đến địa điểm thi muộn hơn so với các đội còn lại.
Hội trường được bố trí ~r \times c~ chiếc ghế được xếp ngay ngắn thành ~r~ hàng và ~c~ cột. Nhìn từ trên cao, các hàng ghế được đánh số từ ~1~ đến ~r~ từ trên xuống dưới, các chiếc ghế trong cùng hàng được đánh số từ ~1~ đến ~c~ theo thứ tự từ trái qua phải. Ta gọi ghế ngồi ở hàng ~i~ và cột ~j~ là ghế ~(i, j)~. Hội trường có một cửa ra vào nằm ở góc trên bên trái.
Hiện tại, các đội thi chính thức đều đã được bố trí chỗ ngồi trong hội trường, sao cho các bạn thuộc cùng một đội sẽ ngồi ở ba ghế liên tiếp nhau trong cùng một hàng. Ban tổ chức (BTC) cần bố trí chỗ ngồi cho đội khách mời bằng cách chọn ra một vị trí hàng ~p~ và cột ~q~ sao cho cả ba ghế ~(p, q)~, ~(p, q+1)~, ~(p, q+2)~ đều chưa có người ngồi. Đồng thời, để tiện cho việc di chuyển vào vị trí của đội khách mời, nếu có nhiều vị trí ngồi khả thi thì BTC sẽ ưu tiên lựa chọn vị trí ngồi có chỉ số hàng ~p~ thấp nhất, nếu vẫn có nhiều vị trí ngồi khả thi trong hàng đó thì BTC sẽ ưu tiên lựa chọn vị trí có chỉ số cột ~q~ nhỏ nhất.
Hãy tìm vị trí ngồi mà BTC đã sắp xếp cho đội khách mời. Dữ liệu vào đảm bảo rằng luôn có cách sắp xếp vị trí ngồi cho đội khách mời.
Input
Dòng đầu tiên gồm hai số nguyên ~r~, ~c~ (~1 \le r \le 100~, ~3 \le c \le 100~) — số hàng ghế và số ghế trong từng hàng.
~r~ dòng tiếp theo, dòng thứ ~i~ chứa xâu ~s_{i,1}, s_{i,2}, \ldots, s_{i,c}~, với ~s_{i,j} =~ 'x' nếu ghế ~(i, j)~ đã có người ngồi và ~s_{i,j} =~ '.' nếu ghế ~(i, j)~ còn trống.
Output
In ra hai số nguyên ~p~ và ~q~ cho biết chỉ số hàng và cột của vị trí ngồi mà BTC đã sắp xếp cho đội khách mời.
Sample Input 1
4 7
xxxxxx.
..xxx..
xxx....
...xxx.
Sample Output 1
3 4
Sample Input 2
3 4
....
....
....
Sample Output 2
1 1
Sample Input 3
3 6
xxxxxx
xxx...
xxxxxx
Sample Output 3
2 4
Sample Input 4
5 4
xxx.
.xxx
xxx.
.xxx
....
Sample Output 4
5 1
Notes
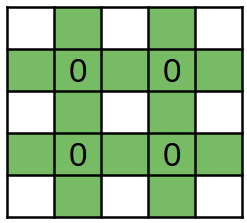
Ở ví dụ thứ nhất, có ba vị trí khả thi cho đội khách mời:
Dòng ~3~, cột ~4~: các bạn sẽ ngồi vào các ghế ~(3, 4)~, ~(3, 5)~, ~(3, 6)~
Dòng ~3~, cột ~5~: các bạn sẽ ngồi vào các ghế ~(3, 5)~, ~(3, 6)~, ~(3, 7)~
Dòng ~4~, cột ~1~: các bạn sẽ ngồi vào các ghế ~(4, 1)~, ~(4, 2)~, ~(4, 3)~
Trong số các vị trí có chỉ số dòng nhỏ nhất ~(3, 4)~, ~(3, 5)~ thì vị trí ~(3, 4)~ có chỉ số cột nhỏ nhất. Do đó, đây là vị trí ngồi mà BTC đã sắp xếp cho đội khách mời.
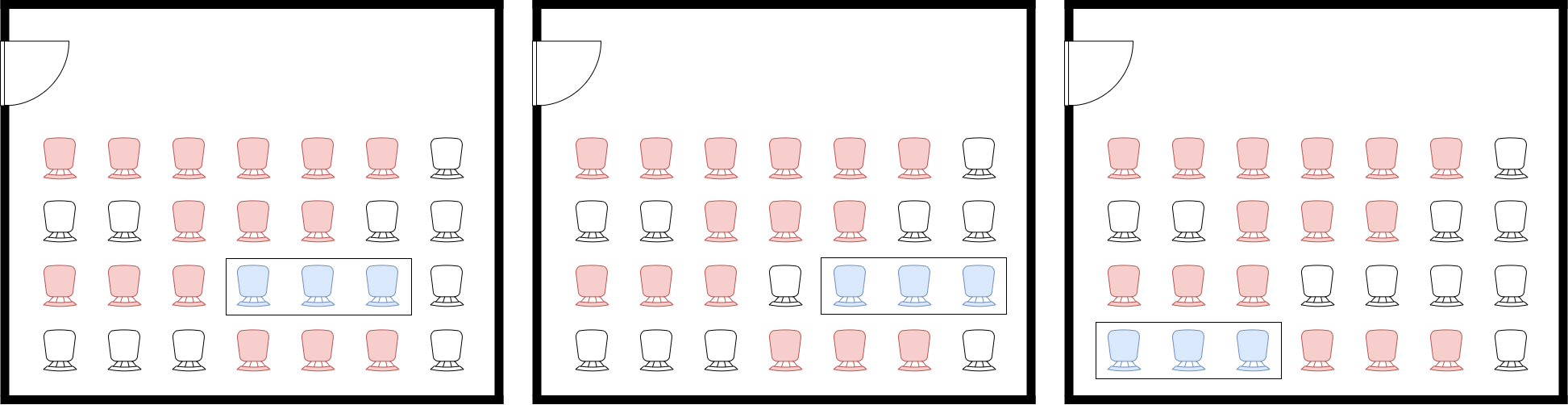
Hình vẽ minh họa ba vị trí khả thi cho đội khách mời ở ví dụ thứ nhất. Màu đỏ biểu thị ghế đã được ngồi, màu xanh biểu thị ghế mà đội khách mời sẽ ngồi.
Điểm: 150
Một công ty thương mại điện tử cung cấp dịch vụ mua gạo trực tuyến. Hôm nay, sau khi nhận các đơn đặt hàng từ các hộ gia đình ở một con phố nọ, công ty tiến hành giao hàng cho các hộ gia đình này.
Để đơn giản, con phố được biểu diễn như trục toạ độ. Có ~n~ đơn hàng mua gạo trực tuyến được đặt. Các đơn hàng được đánh số từ ~1~ đến ~n~, đơn hàng thứ ~i~ yêu cầu giao ~d_i~ bao gạo về hộ gia đình sống tại điểm có toạ độ ~x_i~. Tất cả các hộ gia đình có đơn đặt hàng đều sống ở các điểm có toạ độ dương.
Ngoài ra, trên con phố còn có ~m~ nhà cung cấp gạo, những nơi cung cấp gạo này được đặt tại các điểm có toạ độ dương ~s_1, s_2, \ldots, s_m~. Biết rằng mỗi nhà cung cấp có thể cho ra số lượng gạo lớn tuỳ ý, đồng thời địa điểm của ~n~ hộ gia đình có đơn đặt mua gạo và địa điểm của ~m~ nhà cung cấp gạo là ~n + m~ điểm đôi một phân biệt.
Công ty điều động một xe tải để tiến hành giao gạo cho các hộ dân trên con phố này. Xe tải có sức chứa tối đa ~c~ bao gạo. Xe tải tiến hành giao gạo theo chiến lược sau:
Đầu tiên, xe xuất phát tại bến ở điểm có toạ độ ~0~. Lúc này, trên xe có số gạo đúng bằng sức chứa của xe (tức xe có ~c~ bao gạo).
Xe tiến hành di chuyển theo chiều dương của trục toạ độ. Trong suốt quá trình đi, xe không bao giờ đổi hướng. Nói cách khác, theo thời gian, toạ độ của vị trí của xe chỉ tăng mà không bao giờ giảm.
Khi tới vị trí của một hộ gia đình có đơn đặt mua gạo, nếu trên xe có đủ số gạo để phát cho họ, tài xế sẽ giao đúng số gạo mà đơn hàng yêu cầu. Ngược lại, nếu trên xe không có đủ số gạo mà hộ gia đình yêu cầu, tài xế sẽ bỏ qua đơn hàng và đi tiếp.
Khi tới vị trí của một nhà cung cấp gạo, tài xế sẽ lấy thêm gạo để đưa vào xe cho tới khi số gạo trên xe đúng bằng sức chứa của xe.
Hãy cho biết, với chiến lược giao hàng như trên, có bao nhiêu bao gạo được giao tới các hộ gia đình.
Input
Dòng đầu tiên chứa số nguyên ~\tau~ ~(1 \leq \tau \leq 10)~ là số bộ dữ liệu. Tiếp theo là ~\tau~ bộ dữ liệu, mỗi bộ dữ liệu được mô tả theo khuôn dạng sau:
Dòng đầu tiên chứa ba số nguyên ~c~, ~m~ và ~n~ ~(1 \leq c \leq 10^9, 1 \leq n, m, n + m \leq 10^6)~ lần lượt là số bao gạo tối đa có thể mang lên xe tải, số nhà cung cấp gạo và số đơn đặt hàng.
Dòng thứ hai chứa ~m~ số nguyên ~s_1, s_2, \ldots, s_m~ ~(1 \leq s_i \leq 10^9)~ thể hiện vị trí của các nhà cung cấp gạo.
Trong ~n~ dòng cuối cùng, dòng thứ ~i~ chứa hai số nguyên ~x_i~ và ~d_i~ ~(1 \leq x_i, d_i \leq 10^9)~ lần lượt là vị trí của hộ gia đình đặt hàng và số bao gạo trong đơn hàng thứ ~i~.
Dữ liệu vào đảm bảo ~x_1, x_2, \ldots, x_n~ và ~s_1, s_2, \ldots, s_m~ là ~n + m~ số nguyên đôi một phân biệt.
Output
Với mỗi bộ dữ liệu, in ra một số nguyên dương là tổng số bao gạo được giao đến các hộ gia đình.
Sample Input 1
4
50 2 6
6 10
4 40
8 10
2 20
11 20
9 20
7 30
2 2 3
2 4
1 2
3 2
5 2
1 1 1
1
2 2
2 1 1
2
1 1
Sample Output 1
80
6
0
1
Notes
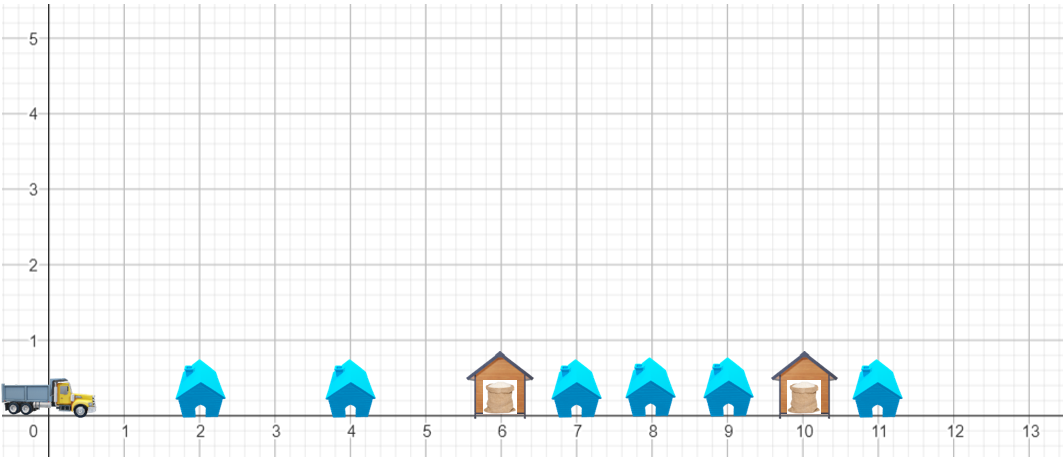
Hình vẽ minh họa bộ dữ liệu 1.
Điểm: 200
Để chuẩn bị cho kế hoạch cải tạo, nâng cấp hạ tầng kết nối Internet trên cả nước, công ty VT tiến hành khảo sát dung lượng Internet sử dụng tại các địa phương.
Cuộc khảo sát được tiến hành trên ~n~ tỉnh và thành phố trực thuộc trung ương trên cả nước. Các thành phố này được đánh số từ ~1~ đến ~n~. Kết quả khảo sát cho thấy tỉnh/thành phố thứ ~i~ có dân số là ~p_i~ và dung lượng Internet sử dụng trong tháng vừa qua tại đây là ~c_i~.
Công ty VT muốn lựa chọn một số địa phương trọng điểm, có nhu cầu sử dụng Internet cao để tiến hành nâng cấp hạ tầng kết nối. Bởi vậy, công ty sẽ chọn ra một nhóm các tỉnh/thành phố trọng điểm, là nhóm các địa phương sao cho dung lượng sử dụng bình quân đầu người của các địa phương này là lớn nhất. Dung lượng Internet sử dụng bình quân đầu người được tính bằng tổng dung lượng Internet sử dụng của các địa phương trong nhóm chia cho tổng dân số của các địa phương trong nhóm.
Nói cách khác, công ty muốn chọn ra một dãy các địa phương ~i_1, i_2, \ldots, i_k~ sao cho:
~k > 0~
~1 \leq i_1 < i_2 < \ldots < i_k \leq n~
Giá trị ~\frac{c_{i_1} + c_{i_2} + \ldots + c_{i_k}}{p_{i_1} + p_{i_2} + \ldots + p_{i_k}}~ lớn nhất.
Hãy giúp công ty tìm ra nhóm địa phương trọng điểm.
Input
Dòng đầu tiên chứa số nguyên ~n~ ~(1 \leq n \leq 50)~ là số tỉnh/thành phố được tiến hành khảo sát.
Dòng thứ hai chứa ~n~ số nguyên ~p_1, p_2, \ldots, p_n~ ~(1 \leq p_i \leq 2 \cdot 10^7)~ lần lượt là dân số của các tỉnh/thành phố trong cuộc khảo sát.
Dòng thứ ba chứa ~n~ số nguyên ~c_1, c_2, \ldots, c_n~ ~(1 \leq c_i \leq 2 \cdot 10^8)~ lần lượt là tổng dung lượng Internet trong tháng vừa qua tại các tỉnh/thành phố được tiến hành khảo sát.
Output
Dòng đầu tiên in ra số nguyên ~k~ ~(1 \leq k \leq n)~ là số tỉnh/thành phố trong nhóm địa phương trọng điểm.
Dòng thứ hai in ra ~k~ số nguyên ~(1 \leq i_1 < i_2 < \ldots < i_k \leq n)~ thể hiện các địa phương trong nhóm trọng điểm này.
Nếu có nhiều nhóm với cùng dung lượng Internet sử dụng bình quân đầu người lớn nhất, bạn có thể in ra một nhóm bắt kỳ.
Sample Input 1
4
10 10 10 10
47 47 47 47
Sample Output 1
3
1 2 4
Sample Input 2
4
1234567 2345678 3456789 4567890
2345678 3456789 4567890 5678901
Sample Output 2
1
1
Sample Input 3
5
98 120 40 135 40
4606 5167 1880 1351 1879
Sample Output 3
2
1 3
Sample Input 4
1
1
20000000
Sample Output 4
1
1
Sau khi xây dựng nhiều khu văn phòng hiện đại, công ty VT đang triển khai lắp đặt hệ thống truyền tin nội bộ cho các khu văn phòng này.
Công ty VT có ~n~ khu văn phòng được đặt tại thành phố X. Các khu văn phòng được đánh số từ ~1~ đến ~n~. Bản đồ thành phố X được mô phỏng trên mặt phẳng toạ độ Descartes và vị trí của ~n~ khu văn phòng lần lượt là ~n~ điểm với toạ độ ~(x_1, y_1)~, ~(x_2, y_2)~, ~\ldots~, ~(x_n, y_n)~. Để xây dựng mạng liên lạc nội bộ cho các khu văn phòng này, công ty VT cân nhắc sử dụng hai phương thức truyền tin: mạng cáp quang và mạng không dây.
Theo đó, công ty có thể lắp đặt một số đường dây cáp quang. Mỗi đường dây sẽ nối hai khu văn phòng với nhau. Công ty dự tính rằng, chi phí lắp đặt cáp quang nối hai khu văn phòng ~i~ và ~j~ là ~c \times d(i, j)~, với ~d(i, j)~ là khoảng cách Euclid giữa hai điểm ~(x_i, y_i)~ và ~(x_j, y_j)~, và ~c~ là hệ số chi phí lắp đặt cáp quang. Đường cáp quang này cho phép việc truyền tin giữa hai khu văn phòng ~i~ và ~j~.
Ngoài ra, công ty có thể lắp đặt một số trạm thu phát sóng ở một số khu văn phòng. Chi phí lắp đặt một trạm thu phát sóng tại một khu văn phòng là giá trị cố định ~w~. Hai khu văn phòng có thể truyền tin trực tiếp cho nhau thông qua mạng không dây nếu tại cả hai khu này đều có trạm thu phát sóng.
Công ty VT muốn lên kế hoạch lắp đặt các đường dây cáp quang và các trạm thu phát sóng sao cho mỗi khu văn phòng có thể truyền tin trực tiếp hoặc gián tiếp tới tất cả ~n - 1~ khu văn phòng còn lại; đồng thời tổng chi phí lắp đặt là nhỏ nhất. Hai khu văn phòng ~i~ và ~j~ có thể truyền tin (trực tiếp hoặc gián tiếp) cho nhau nếu ít nhất một trong ba điều kiện dưới đây được thoả mãn:
Đường dây cáp quang nối hai khu văn phòng ~i~ và ~j~ được xây dựng.
Cả hai khu văn phòng ~i~ và ~j~ đều được lắp trạm thu phát sóng.
Tồn tại một khu văn phòng ~k~ sao cho đồng thời có thể truyền tin giữa hai khu văn phòng ~i~ và ~k~, lại vừa có thể truyền tin giữa hai khu văn phòng ~k~ và ~j~.
Hãy giúp công ty VT tính tổng chi phí lắp đặt nhỏ nhất.
Input
Dòng đầu tiên chứa số nguyên ~n~ ~(1 \leq n \leq 150)~ — số khu văn phòng của công ty VT tại thành phố X.
Trong ~n~ dòng tiếp theo, dòng thứ ~i~ chứa hai số nguyên ~x_i~ và ~y_i~ ~(0 \leq x_i, y_i \leq 10^6)~ thể hiện vị trí của khu văn phòng thứ ~i~.
Dòng cuối cùng chứa hai số thực ~w~ và ~c~ ~(0 \leq w \leq 10^7, 0 \leq c \leq 3)~ lần lượt là chi phí lắp đặt một trạm thu phát sóng và hệ số chi phí lắp đặt cáp quang. Các số thực được cho với không quá ~7~ chữ số ở phần thập phân.
Output
In ra một số thực duy nhất là giá trị nhỏ nhất của tổng chi phí lắp đặt. Đáp án của bạn được chấp nhận nếu sai khác không quá ~10^{-6}~ so với đáp án của ban giám khảo. Nói cách khác, gọi đáp án của ban giám khảo là ~j~ và đáp án của bạn là ~p~, đáp án của bạn được chấp nhận khi và chỉ khi ~\frac{|j - p|}{\max(1, |j|)} \leq 10^{-6}~.
Sample Input 1
4
0 0
0 100
400 0
400 100
150 1.0
Sample Output 1
500.000000000
Sample Input 2
10
798 126
915 25
797 402
463 45
895 841
523 762
959 982
702 605
235 616
523 78
10000000 1.66
Sample Output 2
3358.234405323
Sample Input 3
5
0 0
0 100
400 0
400 100
2000 2000
500 1
Sample Output 3
1600.000000000
Sample Input 4
8
0 0
100 100
200 200
300 300
400 400
2000 2000
2100 2100
2200 2200
200.0000000 0.5000000
Sample Output 4
824.264068712
Notes
Trong ví dụ thứ nhất, phương án tối ưu cho công ty VT là xây dựng đường dây cáp quang nối hai khu văn phòng ~1~ và ~2~, xây dựng đường dây cáp quang nối hai khu văn phòng ~3~ và ~4~; sau đó lắp đặt hai trạm thu phát sóng ở các khu văn phòng ~1~ và ~3~.
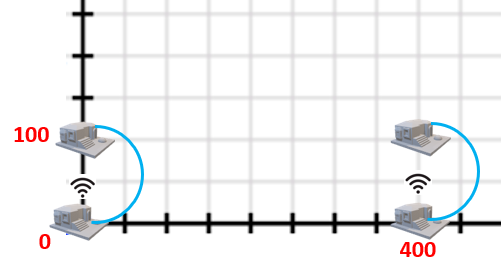
Điểm: 350
Để tăng thêm tinh thần đoàn kết cho các bạn nhân viên, tập đoàn Viettel đã tổ chức một buổi hội trại cho toàn bộ nhân viên trong công ty. Như thường lệ, một hoạt động không thể thiếu của buổi hội trại là trò chơi "Nối vòng tay lớn". Bạn được phân công làm người quản trò cho trò chơi năm nay. Bạn đã đề ra luật chơi của trò chơi năm nay như sau.
~n~ bạn tham gia hội trại còn lại sẽ xếp thành một vòng tròn, các bạn được đánh số từ ~1~ đến ~n~ theo ngược chiều kim đồng hồ. Bạn thứ ~i+1~ sẽ đứng bên phải bạn thứ ~i~, và bạn thứ ~1~ sẽ đứng bên phải bạn thứ ~n~. Ở giữa vòng tròn là một đống sỏi với số lượng viên sỏi rất lớn, luôn đủ để phục vụ cho trò chơi.
Ban đầu, người quản trò sẽ phát cho mỗi bạn một phiếu, phiếu của bạn thứ ~i~ có chứa số ~a_i~ và con số này sẽ quyết định hành động của bạn thứ ~i~ khi đến lượt mình. Sau đó, người quản trò sẽ lấy ~p~ viên sỏi từ đống sỏi trung tâm và chuyền đống sỏi này cho bạn thứ ~1~. Khi đống sỏi được chuyền đến tay của bạn thứ ~i~ thì bạn cần thực hiện hành động sau:
Nếu ~a_i < 0~ thì bạn cần lấy ra ~min(s, -a_i)~ viên sỏi từ đống sỏi trên tay để cho vào đống sỏi trung tâm (với ~s~ là số viên sỏi hiện tại trong đống sỏi)
Nếu ~a_i > 0~ thì bạn cần cho thêm ~a_i~ viên sỏi từ đống sỏi trung tâm vào đống sỏi trên tay
Nếu ~a_i = 0~ thì bạn sẽ không làm gì cả
Sau khi thực hiện hành động trên, nếu đống sỏi còn lại không quá ~q~ viên sỏi thì trò chơi sẽ kết thúc. Ngược lại, bạn cần chuyền đống sỏi trên tay đến cho bạn đứng bên phải mình, và trò chơi được tiếp tục.
Bạn cần tính xem rằng sau bao nhiêu lượt thì trò chơi sẽ kết thúc, hoặc cho biết rằng trò chơi sẽ không bao giờ kết thúc (để từ đó bạn có thể cân nhắc lại luật chơi mà mình đề ra).
Input
Dòng đầu tiên gồm ba số nguyên ~n~, ~p~, ~q~ (~1 \le n, p, q \le 10^5~, ~p > q~) — số bạn tham gia trò chơi, số viên sỏi được đưa cho bạn thứ ~1~ và điều kiện về số viên sỏi kết thúc trò chơi.
Dòng thứ hai gồm dãy số nguyên ~a_1, a_2, \ldots, a_n~ (~-10^5 \le a_i \le 10^5~) — quy định hành động của từng bạn khi đến lượt của mình.
Output
In ra một số nguyên duy nhất là số lượt chơi mà trò chơi sẽ diễn ra, hoặc ~-1~ trong trường hợp trò chơi không bao giờ kết thúc.
Sample Input 1
3 8 3
1 -2 -3
Sample Output 1
5
Sample Input 2
4 9 6
-2 1 -2 3
Sample Output 2
3
Sample Input 3
4 9 5
-2 1 -2 3
Sample Output 3
-1
Sample Input 4
2 100000 1
-1 -1
Sample Output 4
99999
Sample Input 5
2 100 1
-200 100
Sample Output 5
1
Notes
Ở ví dụ thứ nhất, trò chơi sẽ diễn ra trong ~5~ lượt như sau:
Ban đầu, người quản trò sẽ đưa cho bạn thứ nhất đống sỏi gồm ~p = 8~ viên sỏi (hành động này không tính là một lượt chơi).
Với ~a_1 = 1~, bạn thứ nhất sẽ cho thêm ~1~ viên sỏi vào đống sỏi trên tay, và đưa đống sỏi đang có ~9~ viên cho bạn thứ hai.
Với ~a_2 = -2~, bạn thứ hai sẽ lấy ra ~2~ viên sỏi khỏi đống sỏi trên tay, và đưa đống sỏi đang có ~7~ viên cho bạn thứ ba.
Với ~a_3 = -3~, bạn thứ ba sẽ lấy ra ~3~ viên sỏi khỏi đống sỏi trên tay, và đưa đống sỏi đang có ~4~ viên cho bạn thứ nhất.
Với ~a_1 = 1~, bạn thứ nhất sẽ cho thêm ~1~ viên sỏi vào đống sỏi trên tay, và đưa đống sỏi đang có ~5~ viên cho bạn thứ hai.
Với ~a_2 = -2~, bạn thứ hai sẽ lấy ra ~2~ viên sỏi khỏi đống sỏi trên tay. Số viên sỏi lúc này là ~3~, tức là không quá ~q~ viên sỏi nên trò chơi sẽ dừng lại.
Ở ví dụ thứ hai, trò chơi sẽ diễn ra trong ~3~ lượt, và số viên sỏi của đống sỏi trên tay qua từng lượt chơi sẽ thay đổi như sau: ~9 \rightarrow 7 \rightarrow 8 \rightarrow 6~.
Ở ví dụ thứ ba, số viên sỏi của đống sỏi trên tay qua từng lượt chơi như sau: ~9 \rightarrow 7 \rightarrow 8 \rightarrow 6 \rightarrow 9 \rightarrow 7 \rightarrow 8 \rightarrow 6 \rightarrow 9 \rightarrow \ldots~ Có thể thấy rằng trò chơi sẽ không bao giờ kết thúc.
Ở ví dụ thứ năm, bạn thứ nhất sẽ lấy ra toàn bộ ~100~ viên sỏi khỏi đống sỏi trên tay. Đống sỏi không còn lại viên nào, do đó trò chơi kết thúc ngay tại lượt chơi đầu tiên.
Nhóm của Hưng đang viết ứng dụng xử lí dữ liệu văn bản. Văn bản gồm các từ được cho trong tập từ điển gồm ~n~ từ. Mỗi từ là một chuỗi các ký tự chữ cái latin in thường có độ dài không vượt quá 20 ký tự.
Module Hưng đang viết cần xử lí phân tách các từ trong trường hợp người dùng nhập thiếu dấu cách.
Yêu cầu: Cho tập từ điển và các truy vấn, mỗi truy vấn là một xâu người dùng nhập vào bao gồm các chữ cái latin in thường không chứa dấu cách. Hãy đưa ra các từ theo thứ tự sau khi đã phân tách các từ đó, mỗi từ cách nhau bởi một dấu cách.
Input
Dòng đầu chứa số nguyên dương ~n~ là số từ trong từ điển
~n~ dòng tiếp theo, mỗi dòng chứa một từ trong từ điền. (~n≤10^4~)
Dòng tiếp theo chứa số nguyên dương ~q~ là số lượng truy vấn (~q≤100~)
~q~ dòng cuối cùng, mỗi dòng chứa một xâu là xâu người dùng nhập vào không chứa dấu cách. Mỗi xâu có độ dài không quá 500 ký tự.
Output
Đưa ra ~q~ dòng, dòng thứ ~i~ chứa kết quả của truy vấn thứ ~i~. Trường hợp có nhiều cách phân tách, bạn chỉ cần đưa ra một cách trong đó. Đưa ra -1 trong trường hợp không có phương án tách từ phù hợp.
Scoring
Với mỗi test, bạn cần đưa ra đủ ~q~ dòng đáp án. Gọi ~p~ là số câu trả lời đúng trong test, điểm bạn đạt được sẽ là ~p/q~ của test đó. Trường hợp bạn đưa ra khác ~q~ dòng, bạn sẽ không được điểm.
Sample Input 1
8
nam
viet
ha
noi
vo
ho
minh
dich
3
vietnamvodich
vietnamhochiminh
hanoivietnam
Sample Output 1
viet nam vo dich
-1
ha noi viet nam
Sample Input 2
6
an
anh
hai
ai
toi
toia
5
anhai
haian
aianh
toiha
toiaiha
Sample Output 2
an hai
hai an
ai anh
-1
-1
Điểm: 450
Tập đoàn Viettel vừa phát minh ra một loại trạm thu phát sóng mới, cho phép phủ sóng Internet trên một phạm vi rất lớn. Để đánh giá mức độ hiệu quả của phát minh này, ban lãnh đạo tập đoàn Viettel đã quyết định thử nghiệm lắp đặt các trạm phát sóng Internet trên phạm vi toàn thành phố.
Thành phố có thể được mô tả bằng một lưới chữ nhật kích thước gồm ~X~ dòng và ~Y~ cột. Mỗi ô của hình chữ nhật đều có đúng một cư dân sinh sống. Có thể nhận thấy lưới chữ nhật có đúng ~X \times Y~ ô và đồng thời thành phố có đúng ~X \times Y~ cư dân.
Tập đoàn Viettel đã lắp đặt ~N~ trạm phát sóng Internet, trạm phát sóng thứ ~i~ nằm tại ô ~(x_i, y_i)~ và cường độ tín hiệu ~w_i~. Cư dân ở ô ~(x, y)~ sẽ bắt được tín hiệu của trạm phát sóng ~i~ nếu ~\min(|x_i - x|, |y_i - y|) \le w_i~.
Hãy cho biết có bao nhiêu cư dân được phủ sóng Internet trong thành phố. Nói cách khác, hãy đếm số ô ~(x, y)~ sao cho ~1 \le x \le X~, ~1 \le y \le Y~ và từ ô ~(x, y)~ có thể bắt được tín hiệu của ít nhất một trạm phát sóng.
Input
Dòng đầu tiên chứa ba số nguyên ~N~, ~X~, ~Y~ (~1 \le N \le 2 \times 10^5~, ~1 \le X, Y \le 10^9~) cho biết số trạm phát sóng và kích thước của lưới chữ nhật mô tả thành phố.
Dòng thứ ~i~ trong số ~N~ dòng tiếp theo chứa ba số nguyên ~x_i~, ~y_i~, ~w_i~ (~1 \le x_i \le X~, ~1 \le y_i \le Y~, ~0 \le w_i \le \max(X, Y)~) mô tả vị trí và cường độ tín hiệu của trạm phát sóng thứ ~i~. Lưu ý rằng có thể có nhiều trạm phát sóng được đặt cùng một ô.
Hai số trên cùng một dòng cách nhau bởi dấu cách.
Output
In ra một số nguyên duy nhất là số lượng cư dân được phủ sóng Internet.
Scoring
Sample Input 1
3 5 7
1 2 1
4 5 0
4 6 0
Sample Output 1
31
Sample Input 2
4 5 5
2 2 0
2 4 0
4 2 0
4 4 0
Sample Output 2
16
Sample Input 3
4 6 5
1 1 0
1 1 1
6 5 0
6 5 1
Sample Output 3
28
Sample Input 4
5 8 8
2 2 1
2 6 1
6 2 1
6 6 1
3 3 3
Sample Output 4
63
Sample Input 5
2 1000000000 1000000000
1 1 999999999
1000000000 1000000000 999999999
Sample Output 5
1000000000000000000
Notes
Ở ví dụ thứ nhất, chỉ có bốn cư dân không được phủ sóng Internet lần lượt ở các ô ~(3, 4)~, ~(3, 7)~, ~(5, 4)~ và ~(5, 7)~.
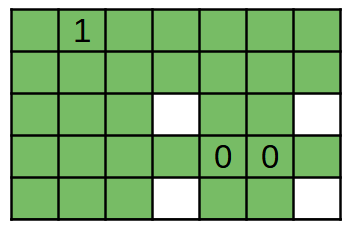
Hình vẽ minh họa ví dụ 1. Các số trong hình vẽ thể hiện vị trí của các trạm phát sóng và cường độ tín hiệu của chúng. Các ô tô màu là các ô được phủ sóng Internet.
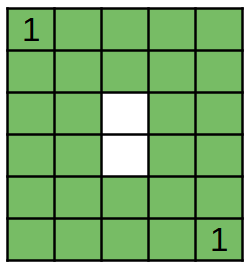
Ở ví dụ thứ hai, có ~16~ cư dân được phủ sóng như trong hình vẽ bên dưới.
Hình vẽ minh họa ví dụ 2.
Ở ví dụ thứ ba, chỉ có hai cư dân ở ô ~(3, 3)~ và ~(4, 3)~ không được phủ sóng Internet. Lưu ý rằng có thể có nhiều trạm phát sóng nằm ở cùng một vị trí.
Hình vẽ minh họa ví dụ 3.
Ở ví dụ thứ tư, chỉ có cư dân ở ô ~(8, 8)~ không được phủ sóng Internet.
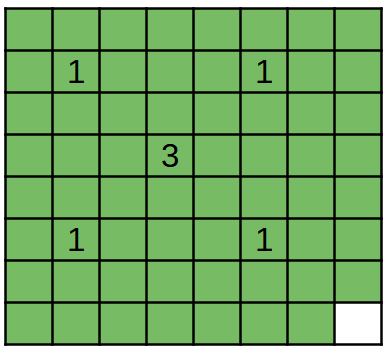
Hình vẽ minh họa ví dụ 4.
Hùng đang được giao nhiệm vụ sắp đặt hàng hoá trong nhà kho. Hàng hoá đã được đóng thành pallet, là các khối vuông kích thước 1 đơn vị. Hiện tại, các pallet được sắp xếp thành các hàng, Hùng sẽ xử lý riêng từng hàng. Mỗi hàng có thể được mô tả bởi một dãy số nguyên không âm ~a=a_1, a_2, \ldots, a_n~, cho biết vị trí thứ ~i~ ở trong hàng này được xếp ~a_i~ pallet chồng lên nhau. Để dễ quan sát và dỡ hàng, Hùng muốn cách sắp đặt thoả mãn tính chất: Các pallet phải được xếp thành các chồng, chồng sau không thấp hơn chồng trước. Cậu có thể thực hiện nhiều thao tác sắp đặt, mỗi thao tác là xếp thêm một pallet vào một chồng nào đó, hoặc dỡ bớt một pallet ở một chồng nào đó. Hùng muốn thực hiện ít nhất các thao tác để đạt được tính chất mong muốn. Cụ thể hơn, bạn được cho một dãy số nguyên không âm ~a=a_1, a_2, \ldots, a_n~. Bạn có thể biến đổi dãy số này, mỗi bước chọn một số trong dãy và tăng số đó lên 1 đơn vị hoặc giảm số đó đi 1 đơn vị, sao cho trong quá trình biến đổi dãy luôn không âm và cuối cùng thu được một dãy không giảm. Hãy tìm số phép biến đổi ít nhất có thể.

Input
Dòng đầu tiên chứa số nguyên dương ~n~ (~1 \leq n \leq 5000~);
Dòng thứ hai chứa ~n~ số nguyên không âm ~a_1, a_2, \ldots, a_n~ (~a_i \leq 10^9\ \forall i=1, 2, \ldots, n~).
Output
Ghi một số tự nhiên là số bước biến đổi ít nhất.
Sample Input 1
5
1 4 2 5 2
Sample Output 1
5
Sample Input 2
9
1 3 5 3 6 3 4 3 7
Sample Output 2
6
Sample Input 3
6
6 5 4 3 2 1
Sample Output 3
9
Sample Input 4
10
1 2 3 4 6 6 8 8 9 10
Sample Output 4
0
Sample Input 5
4
2326153 2340498 6409535 5774211
Sample Output 5
635324
Điểm: 500
Thành phố ABC có ~n~ khu dân cư với ~m~ đường nối 2 chiều đảm bảo liên thông toàn thành phố. Đường đi thứ ~i~ nối 2 khu ~u_i~ và ~v_i~ có thể di chuyển 2 chiều với độ dài ~w_i~. Tại thành phố này, công ty VTEL hoạt động trong lĩnh vực kinh doanh dịch vụ viễn thông luôn chiếm thị phần rất lớn trong lĩnh vực của mình. Công ty vừa ký hợp đồng cung cấp dịch vụ ~k~ khách hàng VIP, khách hàng thứ ~i~ sinh sống ở khu dân cư ~p_i~ (~1≤p_i≤n~ ~∀i=1,2,…,k~). Để đảm bảo hỗ trợ kỹ thuật, giải quyết sự cố, công ty chọn ~k~ nhân viên chăm sóc khách hàng, mỗi nhân viên sẽ phục vụ một khách hàng. Nhân viên thứ ~i~ đang sinh sống tại khu ~q_i~ (~1≤q_i≤n~ ~∀i=1,2,…,k~) và khi nhận được thông tin sự cố sẽ di chuyển từ chỗ ở theo đường đi ngắn nhất qua các khu trung gian tới khu dân cư nơi mà khách hàng của mình đang sinh sống để chăm sóc hỗ sợ. Quãng đường di chuyển bên trong khu dân cư là không đáng kể.
Yêu cầu: Hãy giúp ban lãnh đạo công ty phân công ~k~ nhân viên, mỗi nhân viên hỗ trợ chăm sóc một khách hàng để quãng đường di chuyển của người phải đi xa nhất là ngắn nhất.
Input
Dòng đầu tiên chứa 3 số nguyên dương ~n,m,k~ (~n≤300,m≤5000~)
~m~ dòng tiếp theo, dòng thứ ~i~ chứa 3 số nguyên dương ~u_i~, ~v_i~,~w_i~ xác định thông tin đường nối giữa 2 khu ~u_i~ và ~v_i~ (~u_i,v_i≤n;w_i≤10^6~ ~∀1≤i≤m~). Dữ liệu đảm bảo giữa 2 khu đi chỉ có 1 đường nối duy nhất.
Dòng tiếp theo chứa ~k~ số nguyên ~p_1,p_2,…,p_k~ xác định nơi ở của ~k~ khách hàng.
Dòng cuối cùng chứa ~k~ số nguyên ~q_1,q_2,…,q_k~ xác định nơi ở của ~k~ nhân viên. (~1≤p_j,q_j≤n~ ~∀j:1≤j≤k~)
Output
Dòng đầu tiên ghi số nguyên ~d~ là quãng đường di chuyển của nhân viên phải đi xa nhất theo cách phân công từ nơi ở tới chỗ khách hàng được phân công.
Dòng thứ hai chứa ~k~ số nguyên ~x_1~ ~x_2~ ~x_3~…~x_k~ (~1≤x_i≤k~) với ~x_i~ là số thứ tự của khách hàng mà nhân viên thứ ~i~ được phân công hỗ trợ.
Scoring
Chấm điểm: Bạn cần đưa ra đủ 2 dòng với cấu trúc như trên. Gọi ~d_0~ là đáp án của ban tổ chức. Điểm của bạn nhận được sẽ là ~d_0/d~ số điểm của test đó. Bạn chỉ được điểm trong trường hợp ~k~ số nguyên đưa ra thể hiện cách phân công phù hợp với giá trị ~d~.
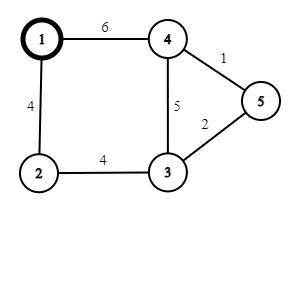
Sample Input 1
5 6 2
1 2 4
3 5 2
5 4 1
3 4 5
3 2 4
1 4 6
1 2
3 5
Sample Output 1
7
2 1
Sample Input 2
5 6 3
1 2 4
3 5 2
5 4 1
3 4 5
3 2 4
1 4 6
1 2 3
3 5 2
Sample Output 2
4
2 3 1
Notes
Giải thích: Ở ví dụ thứ nhất, nhân viên số 1 (khu 3) sẽ chăm sóc khách hàng số 2 (khu 2) với quãng đường 4. Nhân viên số 2 (khu 5) sẽ chăm sóc khách hàng số 1(khu 1) với quãng đường 7.
Ở ví dụ thứ hai, nhân viên số 1 (khu 3) chăm sóc khách hàng số 2 (khu 2) với thời gian di chuyển là 4, nhân viên số 2 (khu 5) chăm sóc khách hàng số 3 (khu 3) với thời gian di chuyển là 2, nhân viên số 3 (khu 2) chăm sóc khách hàng số 1 (khu 1) với thời gian di chuyển là 4.
Điểm: 700
Tải input tại đây: inputs.zip
Với nhu cầu ngày càng lớn sử dụng đồ gia dụng thông minh trong nhà của người Việt Nam, VT lên kế hoạch tham gia vào thị trường này, bắt đầu với việc sản xuất Robot thông minh lau hút bụi nhà. Trước tiên cần đánh giá mức độ khả thi của dự án, công ty đánh giá các bài toán con cần giải quyết để xem nhân sự có đáp ứng được việc tự sản xuất hay không. Một trong các bài toán con cần giải quyết là với mặt sàn của một căn phòng làm sao có thể lập kế hoạch để robot có thể di chuyển được hết mặt sàn của căn phòng. Bài toán được mô hình hoá như sau:
- Coi sàn của căn phòng là một bảng được chia thành lưới ô vuông kích thước ~n\times m~, trong đó sẽ có một số ô có vật cản robot không thể đi vào, còn lại các ô khác trống robot có thể di chuyển thoải mái.
- ~2~ hàng và ~2~ cột là cạnh của bảng tương ứng với các bức tường và robot không thể di chuyển ra được nên các ô trên các vị trí này đều là các vật cản.
- Có một ô là vị trí bắt đầu của robot.
- Robot sẽ di chuyển theo một tập lệnh độ dài ~k~ mô tả hành trình di chuyển của robot.
- Robot sẽ thực hiện lần lượt các lệnh, mỗi lệnh di chuyển robot sẽ di chuyển theo một trong bốn hướng (trên, dưới, trái phải) đến khi gặp vật cản thì dừng lại, sau đó thực hiện lệnh di chuyển tiếp theo.
Bây giờ đội được giao giải quyết bài toán này cần đánh giá xem mức độ hiệu quả mà đội có thể giải quyết bài toán này. Để dễ đánh giá độ hiệu quả, đội sẽ tạo ra một tập lệnh gồm ~k~ lệnh và cho robot di chuyển theo các lệnh này và kiểm tra xem robot có thể di chuyển qua được bao nhiêu ô khác nhau (nếu một ô robot di chuyển qua nhiều lần chỉ được tính một lần).
Yêu cầu: Cho bảng mô tả sàn của một căn phòng, các ô có vật cản, vị trí bắt đầu của robot và số ~k~, hãy tạo ra tập có ~k~ lệnh sao cho robot di chuyển hiệu quả nhất có thể.
Input
Thí sinh được cung cấp ~10~ file dữ liệu đầu vào với tên tương ứng là: input_0.txt, input_1.txt, ..., input_9.txt. Mỗi file dữ liệu đầu vào có khuôn dạng như sau:
- Dòng đầu chứa ba số nguyên ~n, m, k~ (~3 \le n, m, k \le 2000~).
- Tiếp theo là ~n~ dòng mỗi dòng chứa một xâu ~m~ kí tự, với "#" mô tả ô có vật cản, "." là ô trống, "O" là ô xuất phát của robot. Dữ liệu đảm bảo có đúng ~1~ ô "O".
Output
Đối với mỗi file dữ liệu đầu vào, thí sinh cần nộp một file kết quả đầu ra mô tả tập ~k~ lệnh, các file kết quả đầu ra có tên tương ứng là: output_0.txt, output_1.txt, ..., output_9.txt. Mỗi file kết quả đầu ra có khuôn dạng là một chuỗi kí tự có độ dài bằng $k$ gồm các kí tự 'L', 'R', 'U', 'D' tương ứng với:
- 'L' lệnh yêu cầu robot di chuyển về phía bên trái bảng.
- 'R' lệnh yêu cầu robot di chuyển về phía bên phải bảng.
- 'U' lệnh yêu cầu robot di chuyển về phía bên trên bảng.
- 'D' lệnh yêu cầu robot di chuyển về phía bên dưới bảng. -
Chấm điểm
Đối với mỗi test thí sinh sẽ nhận được ~0~ điểm nếu đưa ra output không hợp lệ, ngược lại thí sinh sẽ nhận được như sau: gọi ~S^*~ là số ô robot có thể di chuyển đến trong lời giải của tác giả và ~S~ là số ô robot có thể di chuyển đến trong lời giải của thí sinh, điểm thí sinh nhận được cho mỗi test sẽ là ~\min(1.0, (\frac{S}{S^*})) \times 100~.
Điểm tối đa của một test là ~100~ điểm. Điểm tối đa của bài là ~1000~ điểm.
Điểm của một lần nộp bài là tổng điểm của các test trong bài nộp đó. Điểm của toàn bộ bài là điểm của lần nộp có số điểm cao nhất.
Sample Input
5 5 4
#####
#O#.#
#...#
##..#
#####
Sample Output
DRUD
Giải thích
Với ví dụ trên ta có bảng mô tả sàn nhà!

Lệnh đầu tiên robot sẽ di chuyển xuống dưới bảng

Vị trí của robot sau lệnh di chuyển đầu tiên và thực hiện lệnh thứ hai di chuyển sang phải
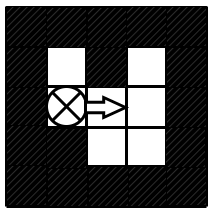
Vị trí của robot sau lệnh di chuyển thứ hai và thực hiện lệnh thứ ba di chuyển lên trên
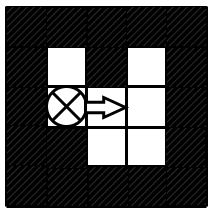
Vị trí của robot sau lệnh di chuyển thứ ba và thực hiện lệnh thứ tư di chuyển xuống dưới
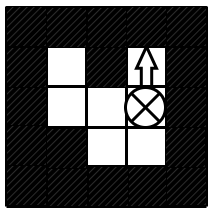
Vị trí kết thúc của robot
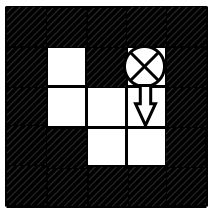
Có ~6~ ô mà robot di chuyển qua
