VNOI CUP 2025 - Vòng loại thứ hai
Sau sự cố tại bài thi sát hạch pháp sư hạng nhất, Hiệp Hội Pháp Sư Châu Lục đã quyết định sẽ vĩnh viễn bỏ bài thi này và thay thế bằng một bài thi tương tự, vừa đòi hỏi khả năng sử dụng ma pháp, vừa yêu cầu tư duy toán học đến từ thí sinh. Bài thi được đề ra như sau:
Sẽ có hai bảng số ~a~ và ~b~, mỗi bảng gồm ~n~ dòng và ~m~ cột được vẽ ra bằng ma pháp. Các dòng được đánh số từ ~1~ đến ~n~ từ trên xuống dưới, các cột được đánh số từ ~1~ đến ~m~ từ trái qua phải.
Trong quá trình thực hiện bài thi, thí sinh có thể dùng ma pháp để thực hiện các phép biến đổi bảng số ~a~ thuộc một trong hai loại sau (với số lần và trình tự tùy ý):
Đảo dọc: Chọn đường cắt giữa hai cột ~y~ và ~y+1~ (~1 \le y < m~). Chia bảng thành hai nửa trái–phải, hoán đổi chúng rồi ghép lại. Khi đó cột ~j \le y~ chuyển thành ~j + (m - y)~, còn cột ~j > y~ chuyển thành ~j - y~.
Đảo ngang: Chọn đường cắt giữa hai dòng ~x~ và ~x+1~ (~1 \le x < n~). Chia bảng thành hai nửa trên–dưới, hoán đổi chúng rồi ghép lại. Khi đó dòng ~i \le x~ chuyển thành ~i + (n - x)~, còn dòng ~i > x~ chuyển thành ~i - x~.
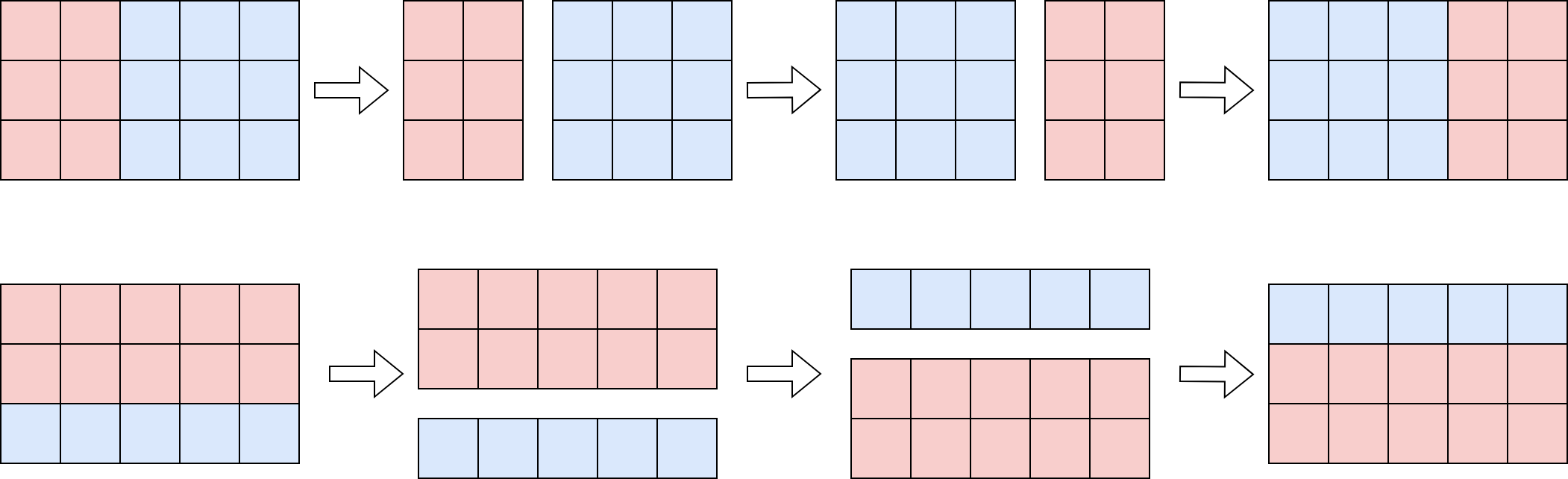
Hình vẽ minh họa hai loại phép biến đổi bảng
Để hoàn thành bài thi, thí sinh cần biến đổi bảng số ~a~ thành bảng số ~b~ chỉ bằng hai loại phép biến đổi trên.
Hãy giúp thí sinh kiểm tra xem có tồn tại cách để hoàn thành bài thi hay không.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên chứa số lượng test case ~t~ (~1 \leq t \leq 50~). Mô tả của mỗi test case như sau.
Dòng đầu tiên gồm hai số nguyên ~n~ và ~m~ (~1 \le n, m \le 50~) – kích thước của hai bảng số.
Dòng thứ ~i~ trong ~n~ dòng tiếp theo gồm ~m~ số nguyên ~a_{i,1}, a_{i,2}, \ldots, a_{i,m}~ (~1 \le a_{i,j} \le 10^4~) – các số trên dòng ~i~ của bảng ~a~.
Dòng thứ ~i~ trong ~n~ dòng tiếp theo gồm ~m~ số nguyên ~b_{i,1}, b_{i,2}, \ldots, b_{i,m}~ (~1 \le b_{i,j} \le 10^4~) – các số trên dòng ~i~ của bảng ~b~.
Dữ liệu vào đảm bảo:
Tổng giá trị ~n~ của các test case không vượt quá ~50~.
Tổng giá trị ~m~ của các test case không vượt quá ~50~.
Output
Với mỗi bộ dữ liệu vào, nếu tồn tại cách biến đổi bảng thỏa yêu cầu đề bài, in ra YES. Ngược lại, in ra NO.
Scoring
Tổng điểm cho bài này là ~500~.
Sample Input 1
2
3 4
1 2 5 2
5 7 4 6
2 3 1 3
3 2 3 1
2 1 2 5
6 5 7 4
2 2
1 1
1 1
1 1
2 2
Sample Output 1
YES
NO
Notes
Ở ví dụ đầu tiên, tồn tại cách biến đổi bảng như sau:
Đảo dọc với đường cắt giữa cột ~1~ và cột ~2~
Đảo ngang với đường cắt giữa dòng ~2~ và dòng ~3~
Đảo dọc với đường cắt giữa cột ~2~ và cột ~3~

Hình vẽ minh họa ví dụ 1
Ở ví dụ thứ hai, dù thực hiện phép biến đổi nào thì bảng ~a~ vẫn sẽ không thay đổi, do đó không tồn tại cách biến đổi bảng ~a~ thành bảng ~b~.
Điểm: 1250
Bạn là một kỹ sư, và bạn đã hạ cánh khẩn cấp trên một hành tinh lạ. Bạn cần xây dựng một nhà máy để trở về không gian. Hiện tại, nhiệm vụ của bạn là nhận các vật thể rơi từ trên trời xuống và thu thập chúng tại một vị trí duy nhất.
Các vật phẩm được thả xuống trong một khu vực, đó là một lưới có kích thước ~n \times m~ (~4 \le n, m~). Các hàng của lưới được đánh số lần lượt từ ~1~ đến ~n~ từ trên xuống dưới, và các cột của lưới được đánh số lần lượt từ ~1~ đến ~m~ từ trái qua phải. Ô giao của hàng thứ ~r~ (~1 \le r \le n~) và cột thứ ~c~ (~1 \le c \le m~) được kí hiệu là ~(r, c)~.
Bạn cần chuyển các vật thể đến ô ~(i, j)~ cho trước. Ngoại trừ ô ~(i, j)~, bạn cần lắp đặt các băng chuyền trên tất cả các ô. Với mỗi băng chuyền, bạn cần chọn một trong bốn hướng lên, xuống, trái hoặc phải để lắp đặt băng chuyền. Băng chuyền tại một ô có thể vận chuyển vật thể nằm trên nó sang ô kề cạnh theo hướng đã được lắp đặt. Bạn cần lắp đặt các băng chuyền thỏa mãn các điều kiện sau:
Nếu có một vật thể rơi tại một ô bất kỳ trên lưới, hệ thống băng chuyền có thể đưa vật thể đến ô ~(i, j)~;
Với mỗi hướng (lên, xuống, trái hoặc phải), cần có ít nhất một băng chuyền được lắp đặt theo hướng này.
Hãy tìm một cách lắp đặt băng chuyền thỏa mãn điều kiện trên. Có thể chỉ ra rằng, với giới hạn đã cho, luôn tồn tại một cách lắp đặt băng chuyền thỏa mãn. Nếu có nhiều cách lắp đặt, hãy tìm một cách lắp đặt bất kỳ.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên của bộ dữ liệu chứa số nguyên dương ~t~ (~1 \le t \le 10\,000~) – số lượng test case. Mô tả của mỗi test case như sau.
Dòng đầu tiên và duy nhất của mỗi test case chứa bốn số nguyên dương ~n~, ~m~, ~i~, ~j~ (~4 \le n, m \le 10^6~, ~1 \le i \le n~, ~1 \le j \le m~) – kích thước của khu vực và chỉ số của ô thu thập.
Đảm bảo rằng tổng của ~n \cdot m~ qua mọi test case không vượt quá ~4 \cdot 10^6~.
Output
Với mỗi test case, hãy in ra ~n~ dòng, mỗi dòng gồm ~m~ kí tự. Kí tự thứ ~c~ trên dòng thứ ~r~ thể hiện cách lắp đặt băng chuyền tại ô ~(r, c)~:
^– thể hiện băng chuyền hướng lên;v– thể hiện băng chuyền hướng xuống;<– thể hiện băng chuyền hướng sang trái;>– thể hiện băng chuyền hướng sang phải;.– thể hiện ô đích. Kí tự này chỉ nên được sử dụng tại ô ~(i, j)~.
Nếu có nhiều cách lắp đặt băng chuyền thỏa mãn, hãy tìm một cách lắp đặt bất kỳ.
Scoring
Tổng điểm cho bài này là ~1250~.
Sample Input 1
2
4 5 3 2
4 4 4 4
Sample Output 1
>>>v<
vv<<^
>.^v<
^^<<^
>>vv
^^v<
>^>v
>>>.
Notes
Ở test case đầu tiên, khi có vật thể được thả xuống ô ~(1, 1)~, nó sẽ được di chuyển đến ô ~(i, j) = (3, 2)~ qua các băng chuyền như sau: $$(1, 1) \xrightarrow{>} (1, 2) \xrightarrow{>} (1, 3) \xrightarrow{>} (1, 4) \xrightarrow{\vee} (2, 4) \xrightarrow{<} (2, 3) \xrightarrow{<} (2, 2) \xrightarrow{\vee} (3, 2)$$
Điểm: 1750
He's a furry little flatfoot, who'll never flinch from a fray-ee-ay-ee-ay!
He's got more than just mad skill,
He's got a beaver tail and a bill,
And the women swoon whenever they hear him say.
He's Perry, Perry the Platypus! Bạn có biết rằng Phineas và Ferb sắp có mùa mới?
Đặc vụ P là một đặc vụ bí mật làm việc cho tổ chức O.W.C.A. (Organization Without a Cool Acronym). Với bộ dạng là một con thú mỏ vịt bình thường, đặc vụ P luôn có hai danh tính mà làm cho kẻ thù của mình là Tiến sĩ Heinz Doofenshmirtz lúc nào cũng nhầm lẫn:
~\mathrm{\color{orange}{A}\ \color{darkcyan}{Platypus}}~ (?) – đây là danh tính thường ngày của đặc vụ P. Nếu như không cải trang thêm gì, Tiến sĩ Doofenshmirtz sẽ nghĩ đặc vụ P chỉ là một con thú mỏ vịt bình thường.
~\mathrm{\color{orange}{Perry}\ \color{brown}{the}\ \color{darkcyan}{Platypus}}~ (?!?) – đây là danh tính mà đặc vụ P sử dụng khi hành động. Tiến sĩ Doofenshmirtz luôn nhận ra ngay đây là đặc vụ P với danh tính này.
Mới đây đặc vụ P đã nhận được một thông điệp từ Tiến sĩ Doofenshmirtz. Thông điệp là một xâu kí tự ~s~ đã được mã hóa, chỉ bao gồm các kí tự a, p và t. Thoạt nhìn qua thì thông điệp có đề cập đến đặc vụ P. Nhưng do không phân biệt được 2 danh tính của đặc vụ, nên lúc thì Tiến sĩ sử dụng ~\mathtt{\color{orange}a\color{darkcyan}p}~, lúc thì dùng ~\mathtt{\color{orange}p\color{brown}t\color{darkcyan}p}~ trong thông điệp của mình.
Đặc vụ P cần nén thông điệp này để gửi về O.W.C.A. phân tích tiếp. Để làm điều này mà không làm mất đi ý nghĩa của thông điệp, đặc vụ P có thể sử dụng một trong hai thao tác sau (không hoặc nhiều lần):
Chọn một xâu con~^*~ ~\mathtt{\color{orange}a\color{darkcyan}p}~ của ~s~ và thay nó bằng ~\mathtt{\color{orange}p\color{brown}t\color{darkcyan}p}~.
Chọn một xâu con ~\mathtt{\color{orange}p\color{brown}t\color{darkcyan}p}~ của ~s~ và thay nó bằng ~\mathtt{\color{orange}a\color{darkcyan}p}~.
Cho thông điệp ~s~ của tiến sĩ Heinz Doofenshmirtz. Hãy giúp đặc vụ P tìm xem, nếu sử dụng hai thao tác trên, thì thông điệp được nén có độ dài nhỏ nhất có thể là bao nhiêu.
~^*~ Xâu ~t~ được gọi là xâu con của ~s~ nếu như ~t~ có thể được tạo thành bằng cách xóa đi (không hoặc nhiều) ký tự ở đầu ~s~, và xóa đi (không hoặc nhiều) ký tự ở cuối ~s~.
Input
Dòng đầu tiên gồm số nguyên ~t~ (~1 \le t \le 10\,000~) – số lượng testcase. Mô tả của mỗi testcase như sau.
Dòng đầu tiên và duy nhất của testcase chứa xâu ~s~ (~1 \le |s| \le 2 \cdot 10^5~, ~s_i \in \{ \mathtt{a}, \mathtt{p}, \mathtt{t} \}~) – thông điệp ban đầu của tiến sĩ Doofenshmirtz.
Đảm bảo rằng tổng ~|s|~ qua các testcase không quá ~2 \cdot 10^5~.
Output
Với mỗi testcase, in ra một số nguyên là độ dài nhỏ nhất của thông điệp đã nén, sử dụng hai thao tác mô tả trong đề bài.
Scoring
Tổng điểm cho bài này là ~1750~.
Sample Input 1
3
ptp
apapapap
aptapt
Sample Output 1
2
8
5
Notes
Trong testcase đầu tiên, thông điệp ~s = \mathtt{ptp}~. Đặc vụ P có thể biến cả thông điệp thành xâu ~s = \mathtt{ap}~, với độ dài xâu là ~2~.
Trong testcase thứ hai, thông điệp ~s = \mathtt{apapapap}~. Có thể chỉ ra rằng đây là thông điệp ngắn nhất có thể, nên đáp án cho testcase thứ hai này là ~8~.
Trong testcase thứ ba, thông điệp ~s = \mathtt{aptapt}~. Đặc vụ P có thể thực hiện nén thông điệp như sau:
~\mathtt{apt\color{orange}a\color{darkcyan}pt} \to \mathtt{apt\color{orange}p\color{brown}t\color{darkcyan}pt}~;
~\mathtt{a\color{orange}p\color{brown}t\color{darkcyan}ptpt} \to \mathtt{a\color{orange}a\color{darkcyan}ptpt}~;
~\mathtt{aa\color{orange}p\color{brown}t\color{darkcyan}pt} \to \mathtt{aa\color{orange}a\color{darkcyan}pt}~.
Điểm: 2250
Sắp tới, chiến dịch airdrop token VNOI sẽ diễn ra trong thời lượng ~n~ giây. Mỗi người dùng, miễn là có tài khoản trên hệ thống VNOJ, đều có thể tham gia. Phần thưởng chia cho mỗi người dùng tham gia sẽ được quy đổi dựa trên số điểm mà người dùng đạt được trong chiến dịch. Khi đăng ký tham gia sự kiện ban đầu, người dùng sẽ nhận được ~s~ điểm mỗi giây từ hệ thống thưởng.
Người dùng có thể sử dụng điểm của mình để đầu tư vào ba danh mục: 1) nâng cấp hệ thống chấm điểm VNOJ, 2) nâng cấp chất lượng bài toán trên VNOJ, và 3) nâng cấp số lượng cuộc thi trên VNOJ. Danh mục đầu tư thứ ~i~ có tối đa ~l_i~ cấp độ đầu tư. Đối với mỗi danh mục, người dùng phải nâng cấp các cấp độ từ thấp nhất đến cao nhất. Để đạt được cấp độ ~j~ của danh mục đầu tư thứ ~i~, người dùng cần tiêu tốn ~c_{i,j}~ điểm. Đổi lại, sau khi nâng cấp, người dùng sẽ nhận thêm ~r_{i,j}~ điểm mỗi giây.
Cụ thể, người dùng bắt đầu ở giây ~0~ với ~0~ điểm. Đối với mỗi giây ~i~ từ ~0~ đến ~n~, hai sự kiện sau sẽ xảy ra theo thứ tự:
Nếu ~i > 0~, người dùng nhận thêm điểm từ hệ thống thưởng.
Người dùng có thể chọn nâng cấp bất kỳ số lượng cấp độ nào cho mỗi danh mục đầu tư, miễn là họ không vượt quá số điểm hiện có. Điều này sẽ làm giảm số điểm (có hiệu lực ngay lập tức), và tăng số điểm thưởng mỗi giây (có hiệu lực bắt đầu từ giây tiếp theo).
Là một nhà đầu tư khôn ngoan, bạn tham gia chiến dịch để tối đa hóa số điểm của mình. Tính toán số điểm tối đa mà bạn có thể nhận được sau khi chiến dịch kết thúc.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên của bộ dữ liệu chứa số nguyên dương ~t~ (~1 \leq t \leq 100~) – số lượng test case. Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa hai số nguyên ~n, s~ (~1 \leq n, s \leq 10^9~) — thời gian của chiến dịch và số điểm ban đầu mà người dùng nhận được mỗi giây.
Tiếp theo là ba nhóm dòng tương ứng với ba danh mục đầu tư, với nhóm dòng thứ ~i~ cho ~3~ danh mục đầu tư như sau.
Dòng đầu tiên chứa một số nguyên dương ~l_i~ (~1 \leq l_i \leq 200~) — số lượng cấp độ đầu tư cho danh mục thứ ~i~.
Dòng thứ hai chứa ~l_i~ số nguyên ~c_{i,1}, c_{i, 2}, ..., c_{i, l_i}~ (~0 \leq c_{i,j} \leq 10^6~) — số điểm cần thiết để nâng cấp các cấp độ của danh mục đầu tư thứ ~i~.
Dòng thứ ba chứa ~l_i~ số nguyên ~r_{i,1}, r_{i, 2}, ..., r_{i, l_i}~ (~0 \leq r_{i,j} \leq 10^6~) — số điểm nhận được mỗi giây sau khi nâng cấp các cấp độ của danh mục đầu tư thứ ~i~.
Đảm bảo rằng ~L_i \le 200~ với mọi ~1 \le i \le 3~, với ~L_i~ là tổng của ~l_i~ qua mọi test case.
Output
Với mỗi test case, in ra một số nguyên duy nhất – cho số điểm tối đa có thể nhận được sau khi chiến dịch kết thúc.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~750~ | ~n \leq 200, L_i \leq 50~ |
| 2 | ~1500~ | Không có ràng buộc bổ sung |
| Tổng | ~2250~ |
Sample Input 1
2
10 5
2
7 4
2 6
1
13
8
3
10 14 23
7 15 11
4 1
7
1 1 1 1 0 1 0
1 1 1 1 0 0 1
1
0
1
7
1 0 1 1 1 0 1
0 1 1 0 1 1 0
Sample Output 1
276
16
Notes
Chiến lược đầu tư tối ưu cho test case đầu tiên như sau:
Ở giây ~0~, bạn không làm gì. Cuối cùng, bạn có ~0~ điểm với tỷ lệ thưởng là ~5~ điểm mỗi giây.
Ở giây ~1~, bạn nhận thêm ~5~ điểm để đạt ~5~ điểm, và bạn không nâng cấp bất kỳ danh mục nào. Cuối cùng, bạn có ~5~ điểm với tỷ lệ thưởng là ~5~ điểm mỗi giây.
Ở giây ~2~, bạn nhận thêm ~5~ điểm để đạt ~10~ điểm. Bạn nâng cấp cấp độ đầu tiên của danh mục thứ ba, điều này tốn của bạn ~10~ điểm. Cuối cùng, bạn có ~0~ điểm với tỷ lệ thưởng là ~12~ điểm mỗi giây.
Ở giây ~3~, bạn nhận thêm ~12~ điểm để đạt ~12~ điểm. Bạn nâng cấp cấp độ đầu tiên và thứ hai của danh mục đầu tiên, điều này tốn của bạn ~11~ điểm. Cuối cùng, bạn có ~1~ điểm với tỷ lệ thưởng là ~20~ điểm mỗi giây.
Ở giây ~4~, bạn nhận thêm ~20~ điểm để đạt ~21~ điểm. Bạn nâng cấp cấp độ thứ hai của danh mục thứ ba, điều này tốn của bạn ~14~ điểm. Cuối cùng, bạn có ~7~ điểm với tỷ lệ thưởng là ~35~ điểm mỗi giây.
Ở giây ~5~, bạn nhận thêm ~35~ điểm để đạt ~42~ điểm. Bạn nâng cấp cấp độ đầu tiên của danh mục thứ hai và cấp độ thứ ba của danh mục thứ ba, điều này tốn của bạn ~36~ điểm. Cuối cùng, bạn có ~6~ điểm với tỷ lệ thưởng là ~54~ điểm mỗi giây.
Trong thời gian còn lại, bạn không nâng cấp thêm bất kỳ danh mục nào. Cuối cùng, bạn nhận được ~(10 - 5) \times 54 + 6 = 276~ điểm.
Điểm: 2750
Với một mảng ~x~ bất kỳ được tạo bởi ~n~ số nguyên dương, ta định nghĩa điểm của mảng ~x~ là
$$\max_{1 \le i < j \le n} \operatorname{LCP}(x_{i:n}, x_{j:n})$$
với ~x_{l:r}~ là mảng con ~[x_l, x_{l + 1}, \ldots, x_r]~ của ~x~, và ~\operatorname{LCP}(b, c)~ trả về độ dài tiền tố chung dài nhất của hai mảng ~b~ và ~c~.
Cho mảng ~a~ gồm ~n~ số nguyên dương. Hãy sắp xếp lại mảng ~a~ sao cho điểm của mảng là lớn nhất có thể.
~\operatorname{LCP}(b, c)~ là hàm trả về ~i - 1~ với ~1 \le i \le \min(|b|, |c|)~ là vị trí đầu tiên sao cho ~b_i \neq c_i~, hoặc trả về ~\min(|b|, |c|)~ nếu vị trí này không tồn tại.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên chứa số lượng test case ~t~ (~1 \le t \le 10^5~). Mô tả của mỗi test case như sau.
Dòng đầu tiên của mỗi test case chứa một số nguyên ~n~ (~2 \le n \le 5 \cdot 10^5~) — độ dài của mảng ~a~.
Dòng thứ hai của mỗi test case chứa ~n~ số nguyên dương ~a_1, \ldots, a_n~ (~1 \le a_i \le n~) – các phần tử của mảng ~a~.
Đảm bảo rằng tổng của ~n~ qua mọi test case không vượt quá ~5 \cdot 10^5~.
Output
Với mỗi test case, hãy in ra hai dòng.
Dòng đầu tiên in ra một số nguyên là số điểm lớn nhất có thể đạt được sau khi sắp xếp các phần tử của ~a~.
Dòng thứ hai in ra ~n~ số nguyên ~a^\prime_1, a^\prime_2, \ldots, a^\prime_n~, với ~a^\prime~ là mảng có thể thu được khi sắp xếp lại các phần tử của mảng ~a~ để thu được số điểm lớn nhất.
Nếu tồn tại nhiều cách sắp xếp mảng để thu được số điểm lớn nhất có thể, hãy tìm một cách bất kỳ.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~500~ | ~1 \le a_i \le 2~ |
| 2 | ~1000~ | Tổng của ~n~ qua mọi test case không quá ~5000~ |
| 3 | ~1250~ | Không có giới hạn gì thêm |
| Total | ~2750~ |
Sample Input 1
6
7
1 3 2 2 1 4 3
7
1 3 2 2 1 4 1
4
1 2 3 4
9
6 6 9 9 6 9 9 9 9
13
11 7 12 7 12 12 12 4 12 7 7 4 7
10
2 1 1 9 1 9 1 2 1 1
Sample Output 1
3
1 3 2 4 1 3 2
3
4 1 2 1 2 1 3
0
1 2 3 4
6
9 6 9 9 6 9 9 6 9
8
11 4 7 12 7 12 7 12 7 12 7 12 4
6
1 1 2 9 1 1 2 9 1 1
Sample Input 2
3
5
1 1 1 1 2
6
2 1 2 1 1 1
32
1 2 1 2 1 2 2 1 1 2 1 1 1 1 2 2 1 1 2 2 1 1 2 1 1 1 2 2 1 2 1 2
Sample Output 2
3
2 1 1 1 1
3
2 2 1 1 1 1
27
1 1 1 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1
Notes
Ở test case thứ nhất, điểm của mảng ~[1, 3, 2, 4, 1, 3, 2]~ là ~3~, vì nếu ta lấy ~i = 1~ và ~j = 5~ thì $$\operatorname{LCP}(a_{i:n}, a_{j:n}) = \operatorname{LCP}([1, 3, 2, 4, 1, 3, 2], [1, 3, 2]) = 3$$ và không có cặp ~i~ và ~j~ nào cho ra kết quả cao hơn. Đây cũng là số điểm tối đa có thể đạt được của bất kỳ cách sắp xếp nào của ~a~. Một cách sắp xếp khác cho ra số điểm là ~3~ là ~[4, 3, 2, 1, 3, 2, 1]~.
Ở test case thứ hai, điểm của mảng ~[4, 1, 2, 1, 2, 1, 3]~ là ~3~, do với ~i = 2~ và ~j = 4~ thì $$\operatorname{LCP}(a_{i:n}, a_{j:n}) = \operatorname{LCP}([1, 2, 1, 2, 1, 3], [1, 2, 1, 3]) = 3$$
Ở test case thứ ba, bất kỳ cách sắp xếp nào cũng cho ra số điểm bằng ~0~.
Điểm: 3500
Nếu bạn đã từng nghe đến các loại tiền mã hóa như Bitcoin hay Ethereum, thì bạn chắc chắn không muốn bỏ lỡ VNOICoin — một đồng coin đặc biệt trong hệ sinh thái VNOI. Điểm đặc biệt của VNOICoin nằm ở cách "đào coin": thay vì sử dụng sức mạnh tính toán để giải các bài toán mã hóa, người tham gia sẽ phải tham gia vào việc tìm ra các dãy hoán vị vui vẻ.
Mỗi khi tạo một khối giao dịch mới, hệ thống VNOICoin sẽ sinh ra một số nguyên dương ~n~, một dãy hoán vị ~b = [b_1, b_2, \dots, b_n]~ của các số từ ~1~ đến ~n~, và một số nguyên tố ~k~.
Một hoán vị ~p = [p_1, p_2, \dots, p_n]~ được gọi là hoán vị vui vẻ tương ứng với ~(b, k)~ nếu ~p~ thỏa mãn điều kiện sau:
~\forall i \in \lbrace 1, 2, \ldots, n \rbrace~, ~k \cdot p_i~ chia hết cho ~b_i~
Ví dụ, với ~b = [1, 2, 3]~ và ~k = 3~, ta có tất cả ~6~ hoán vị của ~p~. Các hoán vị sau đây không phải là hoán vị vui vẻ tương ứng với ~(b, k)~:
~[1, 3, 2]~, do ~k \cdot p_2 = 3 \cdot 3 = 9~ không chia hết cho ~b_2 = 2~;
~[2, 1, 3]~, do ~k \cdot p_2 = 3 \cdot 1 = 3~ không chia hết cho ~b_2 = 2~;
~[2, 3, 1]~, do ~k \cdot p_2 = 3 \cdot 3 = 9~ không chia hết cho ~b_2 = 2~;
~[3, 1, 2]~, do ~k \cdot p_2 = 3 \cdot 1 = 3~ không chia hết cho ~b_2 = 2~;
Hoán vị ~[1, 2, 3]~ và ~[3, 2, 1]~ là hai hoán vị vui vẻ.
Lợi nhuận thu được từ hoán vị vui vẻ ~p~ là số lượng hoán vị vui vẻ ~q~ tương ứng với ~(b, k)~ mà có thứ tự từ điển nhỏ hơn ~p~ ~^*~.
Với ví dụ trên (~b = [1, 2, 3]~, ~k = 3~):
Hoán vị vui vẻ ~[1, 2, 3]~ có lợi nhuận thu được là ~0~, do không có hoán vị vui vẻ khác có thứ tự từ điển nhỏ hơn;
Hoán vị vui vẻ ~[3, 2, 1]~ có lợi nhuận thu được là ~1~, do có duy nhất hoán vị vui vẻ ~[1, 2, 3]~ với thứ tự từ điển nhỏ hơn.
Long — một người đam mê tiền mã hóa — đã tìm được một hoán vị vui vẻ ~p~ tương ứng với ~(b, k)~ đã cho. Tuy nhiên, do hệ thống VNOICoin bị tấn công, nhà phát triển đã triển khai cơ chế bảo mật mới với ~q~ lần cập nhật: Mỗi lần cập nhật sẽ bao gồm việc hoán đổi hai vị trí ~x~ và ~y~ trong cả hai dãy ~p~ và ~b~, tức là đổi chỗ ~p_x~ với ~p_y~ và đồng thời đổi chỗ ~b_x~ với ~b_y~.
Long muốn biết rằng chiến thuật "đào coin" của mình có hiệu quả hay không. Hãy giúp Long xác định nhanh lợi nhuận ban đầu của dãy, cũng như lợi nhuận sau mỗi lần cập nhật. Do giá trị của lợi nhuận có thể rất lớn, hãy in lợi nhuận modulo ~10^9 + 7~.
~^*~Với hai hoán vị ~p~ và ~q~ khác nhau cùng có độ dài ~n~, ta nói ~q~ nhỏ hơn ~p~ theo thứ tự từ điển nếu ~q_i < p_i~, với ~i~ là vị trí đầu tiên mà ~p_i \neq q_i~.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên của bộ dữ liệu chứa số nguyên dương ~t~ (~1 \leq t \leq 10^4~) – số lượng test case. Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa hai số nguyên dương ~n, k, q~ (~2 \le k \le n \leq 10^5~, ~0 \le q \le 10^5~) – độ dài của dãy hoán vị, số nguyên tố ~k~ được tạo ra và số lần thay đổi của dãy.
Dòng thứ hai chứa ~n~ số nguyên dương ~b_i~ (~1 \leq b_i \leq n~) – dãy hoán vị mà VNOICoin tạo ra trong khối giao dịch.
Dòng thứ ba chứa ~n~ số nguyên dương ~p_i~ (~1 \leq p_i \leq n~) – dãy hoán vị vui vẻ mà Long tìm được. Dữ liệu đảm bảo rằng dãy này là một hoán vị vui vẻ tương ứng với ~(b, k)~.
Dòng thứ ~i~ trong ~q~ dòng tiếp theo, mỗi dòng chứa ~2~ số nguyên dương ~x, y~ (~1 \le x, y \le n~, ~x \neq y~), là dữ liệu cho sự điều chỉnh của dãy. Lưu ý rằng các truy vấn là không độc lập với nhau, tức là truy vấn ~i~ sẽ ảnh hưởng tới các truy vấn sau.
Đảm bảo rằng:
Tổng của ~n~ qua các test case không vượt quá ~10^5~,
Tổng của ~q~ qua các test case không vượt quá ~10^5~.
Output
Với mỗi test case, hãy in ra ~q + 1~ số nguyên. Số thứ ~i~ trong đó là giá trị lợi nhuận của dãy ~p~ sau khi ~i - 1~ truy vấn đầu tiên đã được áp dụng theo thứ tự cho bởi input, modulo ~10^9 + 7~.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~500~ | Tổng của ~n~ và ~q~ qua các test case không vượt quá ~2000~, ~\sqrt{n} \lt k \leq n / 2~ |
| 2 | ~750~ | Tổng của ~n~ và ~q~ qua các test case không vượt quá ~2000~ |
| 3 | ~1000~ | ~\sqrt{n} \lt k \leq n / 2~ |
| 4 | ~1250~ | Không có ràng buộc gì thêm |
| Tổng | ~3500~ |
Sample Input 1
2
6 3 3
3 2 4 1 5 6
1 2 4 3 5 6
1 4
1 3
2 6
8 2 4
8 7 2 4 5 1 3 6
4 7 1 8 5 2 3 6
1 4
2 5
1 5
6 8
Sample Output 1
0 2 1 3
2 12 12 2 3
Notes
Ở test case đầu tiên, với ~k = 3~,
Ban đầu, ~b = [3, 2, 4, 1, 5, 6]~ và ~p = [1, 2, 4, 3, 5, 6]~. ~p~ ở đây cũng là hoán vị vui vẻ tương ứng với ~b~ có thứ tự từ điển nhỏ nhất, nên lợi nhuận của Long là ~0~.
Sau truy vấn ~1~, ~b = [\underline{1}, 2, 4, \underline{3}, 5, 6]~ và ~p = [\underline{3}, 2, 4, \underline{1}, 5, 6]~. Tồn tại ~2~ hoán vị vui vẻ bé hơn ~p~ theo thứ tự từ điển là ~[1, 2, 4, 3, 5, 6]~ và ~[1, 6, 4, 3, 5, 2]~, nên lợi nhuận của Long là ~2~.
Sau truy vấn ~2~, ~b = [\underline{4}, 2, \underline{1}, 3, 5, 6]~ và ~p = [\underline{4}, 2, \underline{3}, 1, 5, 6]~. Tồn tại ~1~ hoán vị vui vẻ bé hơn ~p~ theo thứ tự từ điển là ~[4, 2, 1, 3, 5, 6]~, nên lợi nhuận của Long là ~1~.
Sau truy vấn ~3~, ~b = [4, \underline{6}, 1, 3, 5, \underline{2}]~ và ~p = [4, \underline{6}, 3, 1, 5, \underline{2}]~. Tồn tại ~3~ hoán vị vui vẻ bé hơn ~p~ theo thứ tự từ điển là ~[4, 2, 1, 3, 5, 6]~, ~[4, 2, 3, 1, 5, 6]~ và ~[4, 6, 1, 3, 5, 2]~, nên lợi nhuận của Long là ~3~.
Điểm: 4000
MofK muốn nâng cấp cái TV cà tàng của mình bằng cách đem TV đến các tiệm nâng cấp xuyên suốt thành phố anh ấy sống. Thành phố có dạng lưới, với ~n~ con đường chạy ngang và ~m~ con đường chạy dọc. Khi nhìn trên bản đồ, các con đường ngang được đánh số từ ~1~ đến ~n~ từ trên xuống, và các con đường dọc được đánh số từ ~1~ đến ~m~ từ trái qua phải. Giao của đường ngang thứ ~r~ và đường dọc thứ ~c~ được kí hiệu là ~(r, c)~.
MofK xuất phát tại vị trí ~(1, 1)~. MofK sẽ di chuyển trên các con đường, với mục tiêu là đến được Điện Máy Vàng tại vị trí ~(n, m)~. Để đến được Điện Máy Vàng nhanh nhất có thể, tại mỗi bước, từ vị trí ~(r, c)~, MofK sẽ di chuyển đến ô ~(r + 1, c)~ hoặc ~(r, c + 1)~. MofK sẽ không di chuyển ra ngoài thành phố.
May thay, ở mỗi giao lộ đều có một tiệm nâng cấp TV. Khi MofK tiến đến một tiệm nâng cấp (bao gồm cả tiệm nâng cấp tại vị trí xuất phát và Điện Máy Vàng ở vị trí đích), MofK liền mua nâng cấp TV ở tiệm đấy ngay lập tức. Tất nhiên, điều này cũng có nghĩa là chiếc TV sẽ thay đổi kích thước:
Trước khi xuất phát, TV có chiều cao là ~h~ và chiều rộng là ~w~.
Khi được nâng cấp ở tiệm đặt tại giao lộ ~(i, j)~:
Chiều cao của TV tăng thêm ~a_i~;
Chiều rộng của TV tăng thêm ~b_j~.
Trong đó ~a_1, a_2, \ldots, a_n~ và ~b_1, b_2, \ldots, b_m~ là hai dãy số nguyên dương.
MofK muốn kích thước đường chéo TV của mình càng lớn càng tốt. Nói cách khác, trong số tất cả các đường đi hợp lệ để đi từ vị trí ~(1, 1)~ đến ~(n, m)~, hãy giúp MofK tìm ra đường đi mà khi đến Điện Máy Vàng, giá trị ~h^2 + w^2~ (với ~h~ là chiều cao và ~w~ là chiều rộng của TV) là lớn nhất có thể. In ra ~h^2 + w^2~ tại Điện Máy Vàng sau khi MofK thực hiện đi trên con đường đó.
Input
Dòng đầu tiên chứa số nguyên ~t~ (~1 \le t \le 100~) — số lượng test case. Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa bốn số nguyên ~n~, ~m~, ~h~, ~w~ (~1 \le n, m \le 1000~, ~0 \le h, w \le 10^6~) — số lượng con đường ngang, số lượng con đường dọc, chiều cao ban đầu và chiều rộng ban đầu của chiếc TV của MofK.
Dòng thứ hai chứa ~n~ số nguyên ~a_1, a_2, \ldots, a_n~ (~0 \le a_i \le 10^6~) — với ~a_i~ là chiều cao mà TV sẽ tăng lên khi nâng cấp ở bất kỳ tiệm nào trên con đường ngang thứ ~i~.
Dòng thứ ba chứa ~m~ số nguyên ~b_1, b_2, \ldots, b_m~ (~0 \le b_j \le 10^6~) — với ~b_j~ là chiều rộng mà TV sẽ tăng lên khi nâng cấp ở bất kỳ tiệm nào trên con đường dọc thứ ~j~.
Đảm bảo rằng:
tổng ~n~ qua các test case không quá ~1000~;
tổng ~m~ qua các test case không quá ~1000~;
Output
Với mỗi test case, in ra một số nguyên duy nhất là giá trị ~h^2 + w^2~ lớn nhất có thể của MofK khi di chuyển từ vị trí ~(1, 1)~ đến ~(n, m)~ trong số các đường đi hợp lệ.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~500~ | Tổng của ~n~ và ~m~ qua các test case không vượt quá ~50~, đồng thời ~h, w, a_i, b_i \le 50~ |
| 2 | ~1500~ | ~h, w, a_i, b_i \le 1000~ |
| 3 | ~2000~ | Không có ràng buộc gì thêm |
| Tổng | ~4000~ |
Sample Input 1
4
1 3 1 1
2
1 2 3
2 2 10 20
10 20
30 40
2 3 3 1
4 1
5 9 2
10 6 11 9
7 30 49 49 48 10 45 41 37 12
31 34 7 38 19 39
Sample Output 1
98
19400
845
603200
Notes
Ở test case đầu tiên, MofK có một cách đi duy nhất:
Ban đầu, MofK đứng ở ~(1, 1)~. Chiều cao tăng lên ~h = 1 + 2 = 3~, chiều rộng tăng lên ~w = 1 + 1 = 2~.
MofK đi đến ô ~(1, 2)~. Chiều cao tăng lên ~h = 3 + 2 = 5~, chiều rộng tăng lên ~w = 2 + 2 = 4~.
MofK đi đến ô ~(1, 3)~. Chiều cao tăng lên ~h = 5 + 2 = 7~, chiều rộng tăng lên ~w = 4 + 3 = 7~.
Cuối cùng, ~h^2 + w^2 = 7^2 + 7^2 = 98~.
Ở test case thứ hai, cách đi tối ưu của MofK là:
Ban đầu, MofK đứng ở ~(1, 1)~. Chiều cao tăng lên ~h = 10 + 10 = 20~, chiều rộng tăng lên ~w = 20 + 30 = 50~.
MofK đi đến ô ~(1, 2)~. Chiều cao tăng lên ~h = 20 + 10 = 30~, chiều rộng tăng lên ~w = 50 + 40 = 90~.
MofK đi đến ô ~(2, 2)~. Chiều cao tăng lên ~h = 30 + 20 = 50~, chiều rộng tăng lên ~w = 90 + 40 = 130~.
Cuối cùng, ~h^2 + w^2 = 50^2 + 130^2 = 19400~.