VNOI CUP 2025 - Vòng loại thứ nhất
Điểm: 500
Upin và Ipin là hai anh em sinh đôi. Hai cậu rất thân thiết và thường chơi cùng nhau trong những lúc không phải học bài. Hôm nay, họ cùng nhau chơi một trò chơi để thi xem ai có khả năng ghi nhớ tốt hơn. Hai bạn tạo ra một xâu kí tự ~s~ chỉ bao gồm các kí tự U và I. Hai bạn cần chọn ra một xâu con~^*~ ~t~ của ~s~, sao cho ~t~ có chứa ít nhất một kí tự U và ít nhất một kí tự I, và tiến hành chơi trò chơi trên xâu ~t~.
Theo sở trường của mình, Upin có thế mạnh ghi nhớ các kí tự U và Ipin có thể mạnh ghi nhớ các kí tự I. Nếu như gọi ~cnt_\texttt{U}~ và ~cnt_\texttt{I}~ lần lượt là số lượng kí tự U và I trong xâu con ~t~, vậy thì kết của của lượt chơi sẽ được quyết định như sau:
nếu ~cnt_\texttt{U} \geq 2 \cdot cnt_\texttt{I}~, Upin sẽ dành chiến thắng,
nếu ~cnt_\texttt{I} \geq 2 \cdot cnt_\texttt{U}~, Ipin sẽ dành chiến thắng,
nếu như không ai chiến thắng, kết quả của lượt chơi là hòa.
Upin và Ipin giao nhiệm vụ trọng tài cho người bạn tốt của mình là Tpin. Tpin cần phải chọn ra xâu con ~t~. Để cuộc chơi có tính quyết định, Tpin cần phải đảm bảo rằng kết của của cuộc chơi không hòa.
Hãy giúp Tpin tìm ra xâu con ~t~ của xâu ~s~ cho trước thỏa mãn, hoặc chỉ ra rằng mọi cách chọn xâu ~t~ đểu cho ra kết quả hòa. Nếu có nhiều cách chọn xâu ~t~, hãy tìm ra cách chọn bất kì.
————————————————————————
~^*~ Xâu ~t~ được gọi là xâu con của ~s~ nếu như ~t~ có thể được tạo thành bằng cách xóa đi (không hoặc nhiều) ký tự ở đầu ~s~, và xóa đi (không hoặc nhiều) ký tự ở cuối ~s~.
Input
Dòng đầu tiên chứa một số nguyên ~q~ (~1 \leq q \leq 10\,000~) — số lượt chơi. Mô tả dữ liệu của mỗi lượt chơi như sau.
Dòng đầu tiên và duy nhất của mỗi lượt chơi chứa một xâu ~s~ (~|s| \le 10^5~) chỉ gồm các kí tự I và U – mô tả xâu được Upin và Ipin lựa chọn cho lượt chơi thứ ~i~.
Dữ liệu đảm bảo tổng độ dài của các xâu ~s~ trong tất cả các lượt chơi không vượt quá ~10^5~.
Output
Đối với mỗi vòng chơi, in ra NO nếu tất cả các chuỗi con ~t~ dẫn đến hòa.
Nếu không, in ra YES và hai số nguyên ~l, r~ ~(1 \leq l \leq r \leq |S|)~ mô tả cách chọn ~t = s_l s_{l + 1} s_{l + 2} \ldots s_r~.
Nếu có nhiều cách chọn, in ra bất kì cách chọn hợp lệ nào.
Bạn có thể xuất câu trả lời ở bất kỳ kiểu chữ nào (chữ hoa hoặc chữ thường). Ví dụ, các chuỗi "yEs", "yes", "Yes", và "YES" sẽ được công nhận là đúng.
Scoring
Tổng điểm cho bài này là ~500~.
Sample Input 1
4
UUUIIIUIIUI
UU
IUUIIUUI
IU
Sample Output 1
Yes 3 11
No
Yes 2 7
No
Notes
Trong lượt chơi đầu tiên, Tpin chọn xâu con ~t~ = "UIIIUIIUI" có ~cnt_\texttt{I} = 6~ và ~cnt_\texttt{U} = 3~. Ipin sẽ dành chiến thắng do điều kiện ~cnt_\texttt{I} \geq 2 \cdot cnt_\texttt{U}~ thỏa mãn.
Trong lượt chơi thứ hai, Tpin không thể tìm được xâu con ~t~ thỏa mãn.
Trong lượt chơi thứ ba, Tpin chọn xâu con ~t~ = "UUIIUU" có ~cnt_\texttt{I} = 2~ và ~cnt_\texttt{U} = 4~. Upin sẽ dành chiến thắng do điều kiện ~cnt_\texttt{U} \geq 2 \cdot cnt_\texttt{I}~ thỏa mãn.
Trong lượt chơi thứ tư, Tpin không thể tìm được xâu con ~t~ thỏa mãn.
Điểm: 1250
Cho hai số nguyên dương ~n~ và ~m~. Bạn được phép thực hiện thao tác sau (không hoặc nhiều lần):
- Chọn một số ~x~ ~(1 \le x \le m)~ bất kỳ, sau đó gán ~n \leftarrow n \times \gcd(n,x)~. Trong đó ~\gcd(n, x)~ là ước chung lớn nhất của ~n~ và ~x~.
Người dân trên hành tinh Arrakis luôn truyền tai nhau về lời tiên tri, nếu ai tìm được cách biến đổi số ~n~ thành ~m~ bằng cách thực hiện ít thao tác nhất, người đó sẽ trở thành vị cứu tinh của vương quốc, The Messiah. Người thực hiện thử thách này phải đưa ra được một dãy thao tác biến đổi số ~n~ bất kỳ thỏa mãn, hoặc phải chỉ ra rằng không tồn tại cách để biến đổi ~n~ thành ~m~ với thao tác đã cho.
Arrakis đang lâm nguy, thánh chiến sắp nổ ra, hãy thử giải quyết thử thách xem liệu bạn có phải là người được chọn!
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên chứa số lượng test case ~t~ (~1 \le t \le 100~).
Mỗi test case gồm một dòng duy nhất chứa hai số nguyên dương ~n, m~ (~1 \leq n, m \leq 10^9~).
Output
Với mỗi test case, nếu như không tồn tại cách biến đổi số ~n~ thành ~m~ sử dụng thao tác đã cho, in ra ~-1~. Ngược lại, in ra trên một dòng số nguyên ~k~ (~1 \le k \le 200~) — số bước ít nhất để biến đổi ~n~ thành ~m~, theo sau đó là ~k~ số nguyên ~x_1, x_2, \ldots, x_k~ — các số nguyên được chọn cho từng bước theo thứ tự.
Nếu có nhiều dãy thao tác có số bước ít nhất để biến đổi ~n~ thành ~m~, hãy in ra dãy thao tác bất kỳ.
Có thể chỉ ra rằng nếu có thể biến đổi từ ~n~ thành ~m~, sẽ tồn tại dãy biến đổi có không quá ~200~ thao tác.
Scoring
Tổng điểm cho bài này là ~1250~.
Sample Input 1
5
2 2
1 6
6 216
2 12
4 2
Sample Output 1
0
-1
2 6 6
-1
-1
Notes
Ở test case đầu tiên, ~n = m = 2~, do đó không thực hiện thêm thao tác nào.
Ở test case thứ hai, ~n = 1~. Ta chỉ có thể chọn được ~x = 1~, và sau đó gán ~n \gets \gcd(1, 1) = 1~. Thao tác không thể thay đổi ~n~, do đó không tồn tại dãy thao tác hợp lệ.
Ở test case thứ 3, ~n = 6~, ~m = 216~. Trùng hợp thay, ~216 = 6^3~, ta có thể lựa chọn 2 thao tác có ~x~ đều bằng ~6~. Có thể chỉ ra rằng không có dãy thao tác để biến ~n = 6~ thành ~m = 216~ với chỉ 1 thao tác.
Ở test case thứ 5, ~n = 4~, ~m = 2~. Do ~n > m~, và các thao tác không thể giảm số ~n~, nên không tồn tại dãy thao tác thỏa mãn.
Sau khi tốt ngành thời gian học, Kuroni bắt đầu khởi nghiệp và thành lập công ty quản lý thời gian OURO. Sau 1000 năm hoạt động, từ một công ty nhỏ lẻ, OURO đã trở thành công ty quy mô đa vũ trụ. Vừa qua, công ty đã phát hành thêm một loại cổ phiếu mới với lợi nhuận được dự báo sẽ bay lên thẳng mặt trăng.
Có ~n~ cổ đông muốn đầu tư vào loại cổ phiếu này. Các cổ đông được đánh số từ ~1~ đến ~n~. Ban đầu, các cổ đông đều không có cổ phiếu, và tài khoản của họ đều có số tiền bằng ~0~. Có ~q~ sự kiện sẽ diễn ra, các sự kiện thuộc một trong các loại sau:
~\texttt{1} \; p \; x~ — Cổ đông ~p~ mua vào ~x~ cổ phiểu (nếu ~x \ge 0~), hoặc bán đi ~|x|~ cổ phiếu (nếu ~x < 0~);
~\texttt{2} \; v~ — Công ty kinh doanh có lãi, thu về cổ tức ~v~. Mọi cổ đông đang sở hữu cổ phiếu đều thu về số tiền tỉ lệ với số cổ phiếu. Cụ thể, gọi ~s~ là số cổ phiếu mà một cổ đông sở hữu thì số tiền mà tài khoản của cổ đông đó nhận được sẽ tăng thêm ~s \cdot v~.
~\texttt{3} \; p~ — Cổ đông ~p~ sẽ tiến hành rút toàn bộ số tiền hiện có trong tài khoản. Sau khi rút thì số tiền trong tài khoản của cổ đông ~p~ sẽ trở về ~0~.
Với mỗi sự kiện loại ~3~, hãy cho biết số tiền mà cổ đông sẽ thu về được. Vì đáp án có thể rất lớn, bạn có thể in đáp án sau khi chia lấy phần dư cho ~10^9 + 7~.
Input
Dòng đầu tiên gồm hai số nguyên ~n~ và ~q~ (~1 \le n, q \le 5 \cdot 10^5~) — số cổ đông và số sự kiện.
Dòng thứ ~i~ trong ~q~ dòng tiếp theo mô tả sự kiện thứ ~i~ với định dạng như mô tả trong đề bài.
~\texttt{1} \; p \; x~ (~1 \le p \le n~, ~-10^9 \le x \le 10^9~) — mô tả sự kiện loại 1. Đảm bảo rằng sau mỗi sự kiện này, không có cổ đông nào có số cổ phiếu âm.
~\texttt{2} \; v~ (~1 \le v \le 10^9~) — mô tả sự kiện loại 2.
~\texttt{3} \; p~ (~1 \le p \le n~) — mô tả sự kiện loại 3.
Output
Với mỗi sự kiện loại ~3~, in ra số tiền mà cổ đông thu về được sau khi chia lấy phần dư cho ~10^9 + 7~.
Scoring
Tổng điểm cho bài này là ~1500~.
Sample Input 1
3 8
1 1 5
2 3
1 2 10
2 2
3 1
2 4
3 2
3 1
Sample Output 1
25
60
20
Sample Input 2
1 8
1 1 1000
2 1
1 1 -100
2 2
3 1
1 1 -200
2 3
3 1
Sample Output 2
2800
2100
Notes
Trong ví dụ đầu tiên có ~n = 3~ cổ đông. Chỉ có cổ đông ~1~ và ~2~ thực hiện đầu tư.
Bảng dưới đây mô tả các sự kiện có liên quan đến cổ đông ~1~.
| # | Sự kiện | Mô tả | Cổ phiếu | Số dư tài khoản |
|---|---|---|---|---|
| Thời điểm ban đầu | ~0~ | ~0~ | ||
| 1 | 1 1 5 | Cổ đông đầu tư | ~0 + 5 = 5~ | ~0~ |
| 2 | 2 3 | Công ty thu về cổ tức là ~3~ | ~5~ | ~0 + 5 \cdot 3 = 15~ |
| 4 | 2 2 | Công ty thu về cổ tức là ~2~ | ~5~ | ~15 + 5 \cdot 2 = 25~ |
| 5 | 3 1 | Cổ đông thu lời với số tiền là ~25~ | ~5~ | ~0~ |
| 6 | 2 4 | Công ty thu về cổ tức là ~4~ | ~5~ | ~0 + 5 \cdot 4 = 20~ |
| 8 | 3 1 | Cổ đông thu lời với số tiền là ~20~ | ~5~ | ~0~ |
Bảng dưới đây mô tả các sự kiện có liên quan đến cổ đông ~2~.
| # | Sự kiện | Mô tả | Cổ phiếu | Số dư tài khoản |
|---|---|---|---|---|
| Thời điểm ban đầu | ~0~ | ~0~ | ||
| 3 | 1 2 10 | Cổ đông đầu tư | ~0 + 10 = 10~ | ~0~ |
| 4 | 2 2 | Công ty thu về cổ tức là ~2~ | ~10~ | ~0 + 10 \cdot 2 = 20~ |
| 6 | 2 4 | Công ty thu về cổ tức là ~4~ | ~10~ | ~20 + 10 \cdot 4 = 60~ |
| 7 | 3 2 | Cổ đông thu lời với số tiền là ~60~ | ~10~ | ~0~ |
Trong ví dụ thứ hai, có ~n = 1~ cổ đông. Bảng dưới đây mô tả các sự kiện của ví dụ thứ hai.
| # | Sự kiện | Mô tả | Cổ phiếu | Số dư tài khoản |
|---|---|---|---|---|
| Thời điểm ban đầu | ~0~ | ~0~ | ||
| 1 | 1 1 1000 | Cổ đông đầu tư | ~0 + 1000 = 1000~ | ~0~ |
| 2 | 2 1 | Công ty thu về cổ tức là ~1~ | ~1000~ | ~0 + 1000 \cdot 1 = 1000~ |
| 3 | 1 1 -100 | Cổ đông bán cổ phiếu | ~1000 - 100 = 900~ | ~1000~ |
| 4 | 2 2 | Công ty thu về cổ tức là ~2~ | ~900~ | ~1000 + 900 \cdot 2 = 2800~ |
| 5 | 3 1 | Cổ đông thu lời với số tiền là ~2800~ | ~900~ | ~0~ |
| 6 | 1 1 -200 | Cổ đông bán cổ phiếu | ~900 - 200 = 700~ | ~0~ |
| 7 | 2 3 | Công ty thu về cổ tức là ~3~ | ~700~ | ~0 + 700 \cdot 3 = 2100~ |
| 8 | 3 1 | Cổ đông thu lời với số tiền là ~2100~ | ~700~ | ~0~ |
Điểm: 2250
Chắc hẳn bạn nào học tin cũng biết đến câu đố dưới đây khi được học đến phần đệ quy.
Cho một bảng có kích thước ~2^k \times 2^k~ và các mảnh ghép hình chữ L được tạo thành bởi 3 ô vuông. Các mảnh ghép có thể được xoay tùy ý. Tìm cách đặt các mảnh ghép lên bảng sao cho ngoại trừ ô ~(r, c)~, các ô trên bảng đều bị bao phủ bởi chính xác một mảnh ghép.
Bí quyết để giải được câu đố này là cần nhận thấy ta có thể xếp được các mảnh ghép chữ L lớn hơn từ các mảnh ghép nhỏ, và sử dụng các mảnh ghép lớn để lát vào bảng. Để giúp các bạn gợi nhớ, tóm tắt thuật toán tổng quát để giải câu đố này sẽ được mô tả lại ở phần chú thích phía dưới.
Sau khi giảng cho bạn thuật toán này, thầy giáo đã rất kinh ngạc khi thấy bạn đã hiểu và có khả năng áp dụng nó rất nhanh. Thầy giáo đành phải ra thêm bài tập bổ sung xoay quanh thuật toán này. Cho một bảng có kích thước ~2^k \times 2^k~. Các hàng được đánh số ~0, 1, 2, \ldots, 2^k - 1~ từ trên xuống dưới, và các cột được đánh số ~0, 1, 2, \ldots, 2^k - 1~ từ trái qua phải. Ban đầu bảng đã được lát bằng các mảnh ghép chữ L sao cho ô ~(0, 0)~ là ô không bị bao phủ theo như thuật toán bạn đã được học.
Sau đó thầy giáo có ~q~ câu đố nhỏ liên tiếp. Với câu đố thứ ~i~, thầy giáo muốn biến bảng, từ trạng thái ngay trước câu đố này, đến trạng thái mà bảng có ô ~(r_i, c_i)~ không được bao phủ. Để làm điều này thầy giáo cho bạn thực hiện thao tác sau (không hoặc nhiều lần):
- Chọn một mảnh ghép chữ L mà đang kề với 2 cạnh của ô không được bao phủ. Xoay mảnh ghép này đi 90 độ theo chiều mà bạn muốn. Có thể thấy sau thao tác này, một ô mới sẽ trở thành ô không được bao phủ.
Có thể chỉ ra rằng, với cách lát ban đầu theo như thuật toán mà bạn đã được học, lúc nào cũng tồn tại dãy thao tác xoay các mảnh ghép, để biến bảng có ô chưa bao phủ từ một ô này đến một ô khác.
Dưới đây là minh họa cách thực hiện thao tác cho bảng ~2^2 \times 2^2~. Thầy giáo đã ra ba câu đố, với mỗi câu cần biến đổi ô không bao phủ như sau:
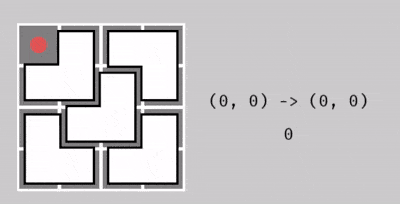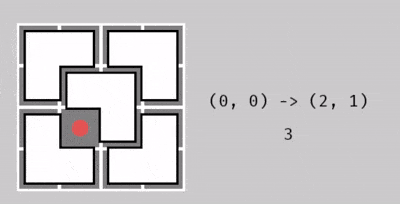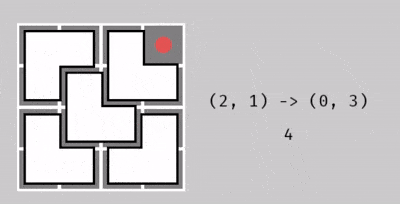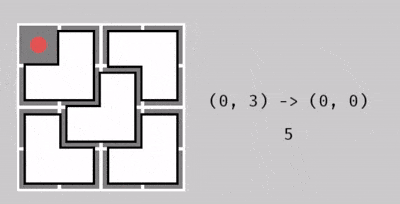
Từ ô ~(0, 0)~ thành ô ~(2, 1)~, với 3 thao tác.
Từ ô ~(2, 1)~ thành ô ~(0, 3)~, với 4 thao tác.
Từ ô ~(0, 3)~ thành ô ~(0, 0)~, với 5 thao tác.
Thầy giáo muốn bạn giải đáp các câu đố càng nhanh càng tốt. Do đó với mỗi câu đố, bạn muốn tìm xem cần thực hiện ít nhất bao nhiêu thao tác để đáp câu đố đó.
Input
Dòng đầu tiên gồm hai số nguyên ~k~ và ~q~ (~1 \le k \le 60~, ~1 \le q \le 10^5~). Tham số ~k~ cho biết kích thước của bảng là ~2^k \times 2^k~, và thầy giáo sẽ hỏi bạn ~q~ câu đố.
Dòng thứ ~i~ trong ~q~ dòng tiếp theo chứa hai số nguyên ~r_i~ và ~c_i~ (~0 \le r_i, c_i < 2^k~) – ô không được bao phủ sau câu đố thứ ~i~.
Output
In ra ~q~ dòng. Dòng thứ ~i~ chứa một số nguyên là số thao tác ít nhất để giải đáp câu đố thứ ~i~.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~500~ | ~k \le 5~, ~q \le 1000~ |
| 2 | ~750~ | ~k \le 10~ |
| 3 | ~1000~ | Không có ràng buộc gì thêm |
| Tổng | ~2250~ |
Sample Input 1
2 3
2 1
0 3
0 0
Sample Output 1
3
4
5
Sample Input 2
3 4
6 2
7 7
3 4
4 6
Sample Output 2
10
10
7
5
Notes
Ví dụ đầu tiên đã được minh họa qua hình ở phía trên.
Dưới đây là minh họa cho ví dụ thứ hai.
Tóm tắt thuật toán lát các mảnh ghép chữ L
Từ các mảnh ghép chữ L nhỏ, ta có thể tạo ra các mảnh ghép cũng có hình chữ L to hơn theo cách ghép sau:
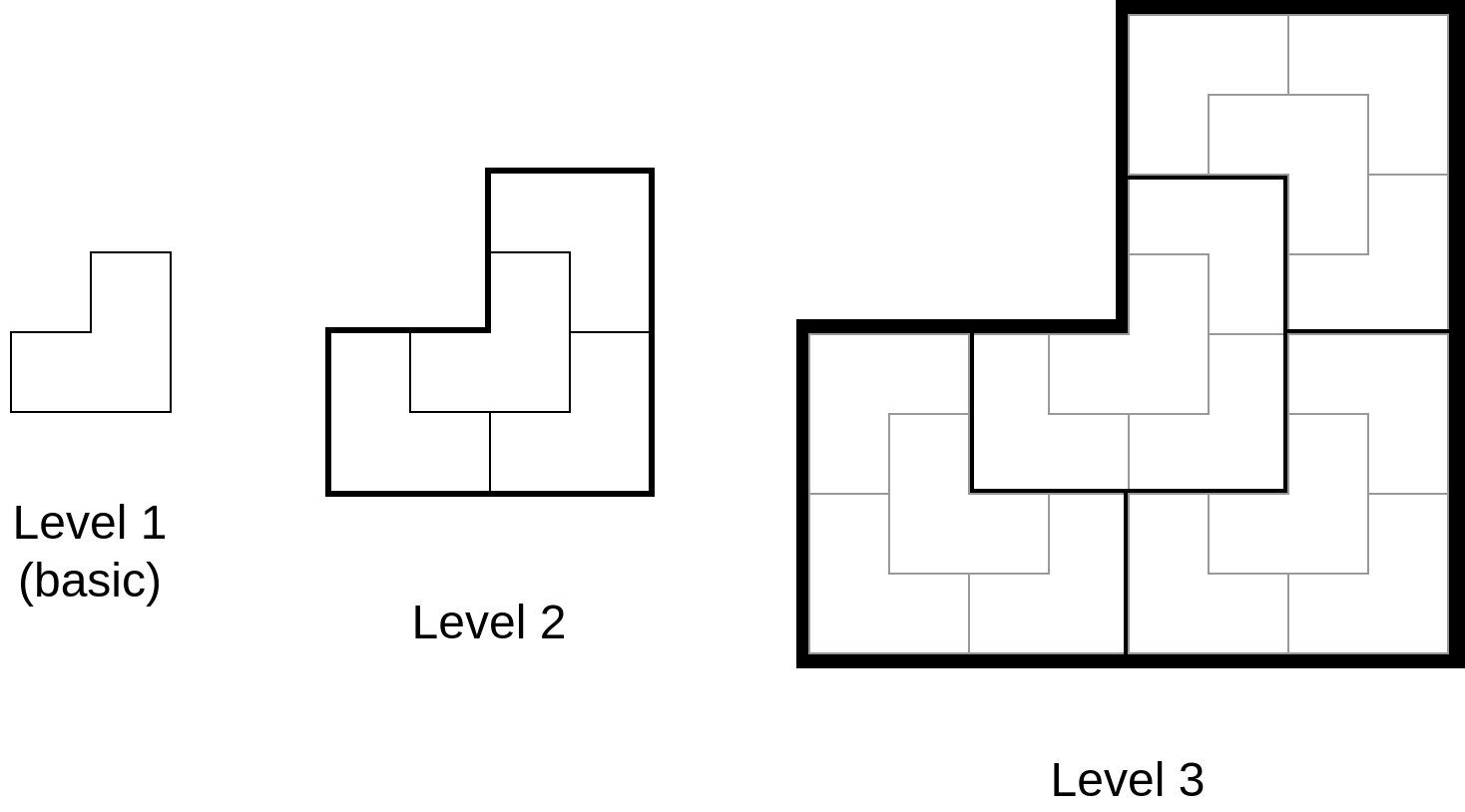
Để lát các mảnh ghép chữ L vào bảng, sao cho ô ~(0, 0)~ không bị bao phủ, ta có thể ghép chúng thành các mảnh ghép chữ L to hơn và chồng chúng lên như sau:
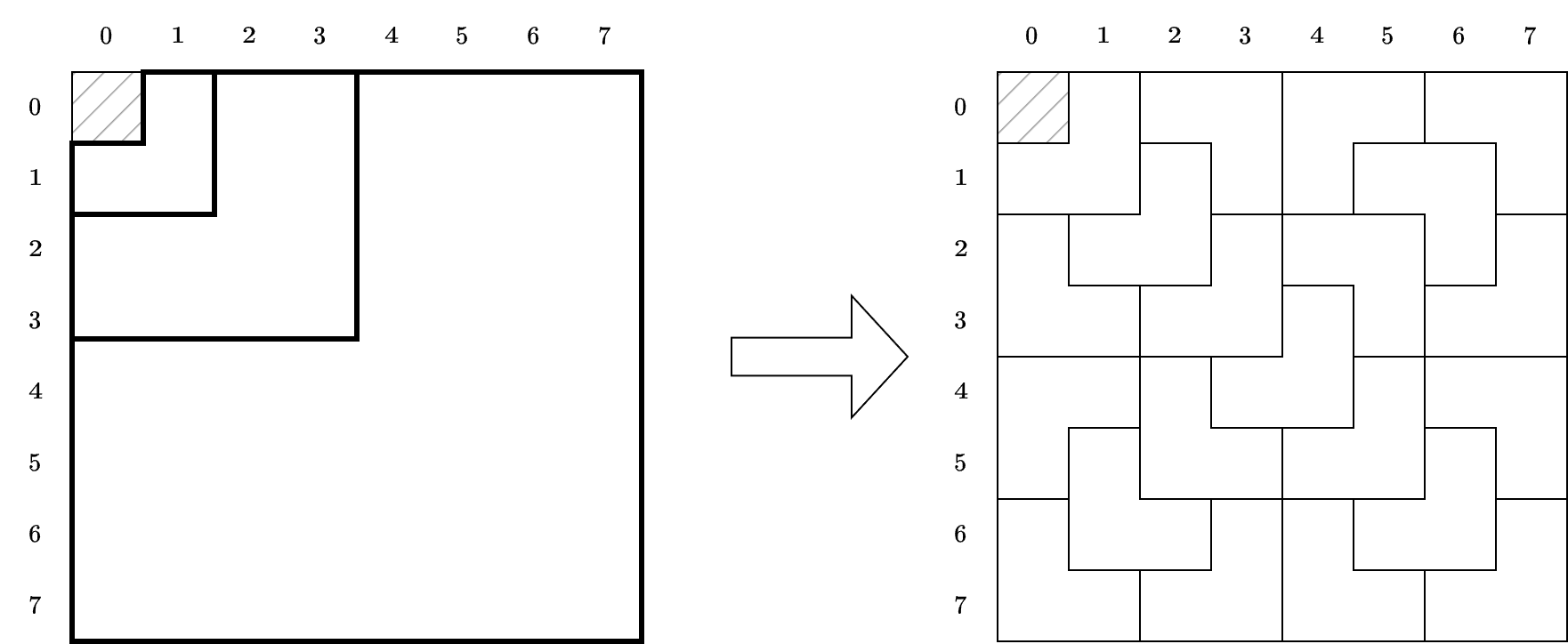
Điểm: 2750
Cho số nguyên dương ~k~ và một mảng ~a~ gồm ~n~ số nguyên không âm nhỏ hơn ~2^k~. Đối với mỗi hoán vị~^*~ ~p~ gồm ~n~ phần tử từ ~1~ đến ~n~, định nghĩa:
~f_i(p) = a_{p_1}\ \&\ a_{p_2}\ \& \ldots \&\ a_{p_{i-1}}\ \&\ a_{p_i}~ với ~1 \le i \le n~, trong đó ~\&~ là phép toán AND bit,
~g(p)~ là chỉ số ~1 \le i \le n~ lớn nhất sao cho ~f_i(p) > 0~. Nếu như ~f_i(p) = 0~ với mọi ~1 \le i \le n~ thì ~g(p) = 0~.
Tính tổng của ~g(p)~ qua tất cả các hoán vị ~p~, modulo ~998\,244\,353~.
———————————————————————–
~^*~ Một hoán vị gồm ~n~ phầnt từ từ ~1~ đến ~n~ là dãy số chứa các số ~1, 2, \ldots, n~ theo thứ thự bất kì. Ví dụ ~[1, 3, 2, 4]~ và ~[5, 4, 1, 2, 3]~ là các hoán vị, nhưng ~[1, 4, 2]~ và ~[1, 4, 2, 2, 5]~ thì không.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên chứa số lượng test case ~t~ (~1 \le t \le 10\,000~). Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa hai số nguyên ~n~ và ~k~ (~1\le n \le 2^{20}~, ~1 \le k \le 20~) – số lượng phần tử của ~a~ và giới hạn của các phần tử của ~a~ là ~2^k~.
Dòng thứ hai chứa ~n~ số nguyên không âm ~a_1,a_2,\ldots,a_n~ (~0\le a_i<2^k~).
Đảm bảo rằng:
tổng của ~n~ qua tất cả các test case không vượt quá ~2^{20}~,
tổng của ~2^k~ qua tất cả các test case không vượt quá ~2^{20}~.
Output
Với mỗi test case, in ra một số nguyên — tổng của ~g(p)~ qua tất cả các dãy ~p~, theo modulo ~998\,244\,353~.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~250~ | ~k = 1~ |
| 2 | ~500~ | ~\sum n \le 2^{10}~ |
| 3 | ~500~ | ~\sum 2^k \le 2^{10}~ |
| 4 | ~1500~ | Không có ràng buộc gì thêm |
| Tổng | ~2750~ |
Sample Input 1
2
3 1
1 0 1
8 3
0 1 2 3 4 5 6 7
Sample Output 1
6
67248
Notes
Kí hiệu ~a_p = [a_{p_1}, a_{p_2}, \ldots, a_{p_n}]~.
Ở test case đầu tiên, ta có ~a = [1, 0, 1]~.
Có 2 hoán vị ~p~ với ~g(p) = 1~ là ~p = [1, 2, 3]~ và ~p = [3, 2, 1]~. Chúng đều có ~a_p = [1, 0, 1]~.
Có 2 hoán vị ~p~ với ~g(p) = 2~ là ~p = [1, 3, 2]~ và ~p = [3, 1, 2]~. Chúng đều có ~a_p = [1, 1, 0]~.
Các hoán vị ~p~ còn lại có ~g(p) = 0~.
Đáp án cho test case là ~2 \cdot 1 + 2 \cdot 2 = 6~.
Ở test case thứ hai, ta có ~a~ là hoán vị của ~8~ số nguyên từ ~0~ đến ~7~. Bảng dưới đây thể hiện số lượng các hoán vị ~p~ nhóm theo giá trị ~g(p)~.
| ~g(p)~ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| # | 5040 | 13680 | 12960 | 6912 | 1728 | 0 | 0 | 0 | 0 |
Dựa vào bảng trên, đáp án cho test case là: $$5040 \cdot 0 + 13680 \cdot 1 + 12960 \cdot 2 + 6912 \cdot 3 + 1728 \cdot 4 + 0 \cdot 5 + 0 \cdot 6 + 0 \cdot 7 + 0 \cdot 8 = 67248$$
Vương quốc Pekoland có ~n~ thành phố được đánh số từ ~1~ đến ~n~. Một ngày ở Pekoland được chia thành ~10^9~ đơn vị thời gian, trong đó thời điểm ~0~ là nửa đêm. Người dân Pekoland chủ yếu di chuyển giữa các thành phố bằng máy bay. Hàng ngày, có ~m~ chuyến bay ở Pekoland, trong đó chuyến bay thứ ~i~ khởi hành tại thành phố ~u_i~ vào thời điểm ~x_i~ và hạ cánh tại thành phố ~v_i~ vào thời điểm ~y_i~. Nhờ hạ tầng tối tân, việc làm thủ tục tại các sân bay mất thời gian không đáng kể, do vậy một hành khách tới thành phố ~u~ vào thời điểm ~t~ có thể chọn bay tiếp bất kỳ chuyến bay nào xuất phát tại ~u~ từ thời điểm ~t~ trở đi.
Có hai hãng hàng không hoạt động ở Pekoland, và mọi chuyến bay ở đây đều được khai thác bởi một trong hai hãng này. Pekoland Airlines là hãng hàng không hoàng gia, mọi chuyến bay của Pekoland Airlines đều đảm bảo bay đúng kế hoạch. Ngược lại, PekoJet Air là một hãng hàng không giá rẻ mới thành lập, những chuyến bay của hãng này có thể bị hủy mà không báo trước. Dù vậy, PekoJet Air cam kết mỗi ngày chỉ có tối đa ~k~ chuyến bay bị hủy.
Aqua là một du khách nước ngoài. Cô vừa đáp xuống thành phố ~1~—kinh đô của Pekoland—vào nửa đêm (thời điểm ~0~). Aqua muốn bay tới thành phố ~n~, nơi chuẩn bị kỷ niệm ~50~ năm ngày thống nhất vương quốc vào ngày mai. Giả sử Aqua đang ở thành phố ~u~ vào thời điểm ~t~, cô có thể chọn làm thủ tục cho một trong các chuyến bay khởi hành từ ~u~ vào thời điểm ~t~, hoặc chọn không làm gì (đợi đến thời điểm ~t+1~). Nếu có nhiều chuyến bay cùng khởi hành một lúc, Aqua chỉ có thể chọn một chuyến bay để làm thủ tục, và cô chỉ có thể biết chuyến bay đó có bị hủy hay không sau khi đã làm thủ tục xong. Nếu chuyến bay bị hủy, cô sẽ ở lại thành phố ~u~ ở thời điểm ~t+1~, ngược lại cô sẽ hạ cánh ở thành phố đích theo đúng lịch trình của chuyến bay.
Để tìm được vị trí ưng ý nhất trong buổi diễu hành vào sáng ngày hôm sau, Aqua muốn đến thành phố ~n~ trong ngày và sớm nhất có thể. Cụ thể, Aqua muốn biết thời điểm ~x~ nhỏ nhất sao cho cô có thể đến ~n~ vào trước hoặc đúng thời điểm ~x~, bất kể những chuyến bay nào bị hủy. Nếu Aqua không thể chắc chắn đến ~n~ trong ngày, in ra ~-1~. Hãy giúp Aqua nhé!
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên chứa số lượng test case ~t~ (~1 \leq t \leq 10\,000~). Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa ba số nguyên ~n~, ~m~, ~k~ (~2 \leq n \leq 10^5~, ~1 \leq m \leq 2 \cdot 10^5~, ~0 \leq k \leq m~) — số thành phố ở Pekoland, số chuyến bay hàng ngày ở Pekoland, và số chuyến bay tối đa của PekoJet Air có thể bị hủy trong ngày.
Dòng thứ ~i~ trong ~m~ dòng tiếp theo chứa năm số nguyên ~u_i~, ~v_i~, ~x_i~, ~y_i~, ~p_i~ (~1 \leq u_i, v_i \leq n~, ~u_i \neq v_i~, ~0 \leq x_i < y_i < 10^9~, ~1 \leq p_i \leq 2~) mô tả một chuyến bay. Chuyến bay thứ ~i~ khởi hành tại thành phố ~u_i~ vào thời điểm ~x_i~ và hạ cánh tại thành phố ~v_i~ vào thời điểm ~y_i~. Chuyến bay thứ ~i~ được khai thác bởi Pekoland Airlines nếu ~p_i = 1~ và PekoJet Air nếu ~p_i = 2~.
Đảm bảo rằng:
tổng của ~n~ qua tất cả các test case không vượt quá ~10^5~,
tổng của ~m~ qua tất cả các test case không vượt quá ~2 \cdot 10^5~.
Output
Với mỗi test case, in ra thời điểm ~x~ nhỏ nhất sao cho cô có thể đến ~n~ vào trước hoặc đúng thời điểm ~x~, bất kể những chuyến bay bị hủy ra sao. Nếu Aqua không thể chắc chắn đến ~n~ trong ngày, in ra ~-1~.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~500~ | ~p_i = 1~ với mọi ~1 \leq i \leq m~ |
| 2 | ~1000~ | ~\sum n \le 1\,000~, ~\sum m \le 1\,000~ |
| 3 | ~1750~ | Không có ràng buộc gì thêm |
| Tổng | ~3250~ |
Sample Input 1
3
2 4 1
1 2 0 12 1
1 2 2 10 2
1 2 3 7 2
1 2 3 4 2
5 6 1
1 2 1 5 1
1 3 1 5 1
1 4 1 5 1
2 5 5 10 2
3 5 5 10 2
4 5 5 10 2
4 7 2
1 2 0 2 2
1 3 1 3 1
2 3 2 3 2
2 4 4 6 1
3 2 3 4 2
3 4 4 7 2
3 4 5 7 2
Sample Output 1
10
-1
7
Notes
Trong ví dụ thứ nhất, Aqua có thể đến thành phố ~2~ chậm nhất vào thời điểm ~10~ theo kế hoạch sau:
Bỏ qua chuyến bay ~1~, làm thủ tục chuyến bay ~2~ ở thời điểm ~2~.
Nếu chuyến bay ~2~ không bị hủy, Aqua đáp xuống thành phố ~2~ ở thời điểm ~10~.
Ngược lại, Aqua làm thủ tục chuyến bay ~4~. Chuyến bay này chắc chắn không bị hủy do chuyến bay ~2~ đã bị hủy, do đó Aqua đáp xuống thành phố ~2~ ở thời điểm ~4~.
Lưu ý rằng, nếu Aqua không làm thủ tục cho chuyến bay ~2~ thì cô không thể đảm bảo đến được thành phố ~2~, do chuyến bay ~3~ và ~4~ khởi hành cùng giờ và cô chỉ có thể chọn làm thủ tục cho một trong hai chuyến bay này (và chuyến bay cô chọn luôn có thể bị hủy).
Dưới đây là minh họa cho ví dụ đầu tiên:
Cạnh màu xanh là chuyến bay của hãng ~\color{blue}{Pekoland\,Airlines}~.
Cạnh màu đỏ là chuyến bay của hãng ~\color{red}{PekoJet\,Air}~.
Số màu xanh lá cây trên cạnh là thời điểm cất cánh của chuyến bay ~\color{green}{x_i}~.
Số màu cam trên cạnh là thời điểm hạ cánh của chuyến bay ~\color{orange}{y_i}~.
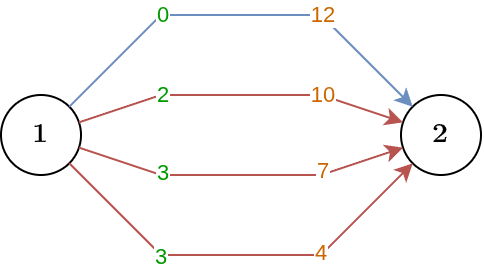
Minh họa cho ví dụ đầu tiên
Trong ví dụ thứ hai, Aqua có thể chọn bay tới thành phố ~2~, ~3~, hoặc ~4~ ở thời điểm ~5~. Tuy nhiên, bất kể cô chọn thành phố nào, chuyến bay duy nhất nối thành phố đó và thành phố ~5~ đều có thể bị hủy. Do đó, đáp án là ~-1~.
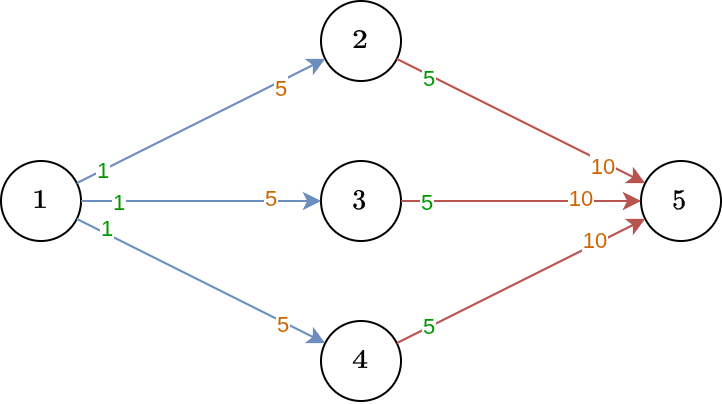
Minh họa cho ví dụ thứ hai
Trong ví dụ thứ ba, hãng PekoJet Air đảm bảo rằng không quá 2 chuyến bay sẽ bị hủy. Aqua có thể đến được thành phố ~4~ muộn nhất tại thời điểm ~7~.
Tại thành phố ~1~, thời điểm ~0~, Aqua có thể thử làm thủ tục cho chuyến bay của hãng PekoJet Air.
Nếu chuyến bay không bị hủy, Aqua có thể đi tiếp đến thành phố ~4~ bằng chuyến bay của hãng Pekoland Airlines tại thời điểm ~6~. Aqua đã đến đích.
Nếu chuyến bay bị hủy, Aqua đến thành phố ~3~ tại thời điểm ~3~ với chuyến bay của hãng Pekoland Airlines.
Khi ở thành phố ~3~ ở thời điểm ~3~, Aqua có thể thử chuyến bay của hãng PekoJet Air đến thành phố ~2~.
Nếu chuyến bay không bị hủy, Aqua có thể đi tiếp đến thành phố ~4~ bằng chuyến bay của hãng Pekoland Airlines tại thời điểm ~6~. Aqua đã đến đích.
Nếu chuyến bay bị hủy, Aqua ở lại thành phố ~3~ và xét chuyến bay đến thành phố ~4~.
Đến lúc này, PekoJet Air đã hủy 2 chuyến bay, do đó hãng không thể hủy thêm chuyến bay nào nữa.
Aqua có thể bắt chuyến bay bất kỳ của hãng PekoJet Air đến thành phố ~4~ tại thời điểm ~7~. Aqua đã đến đích.
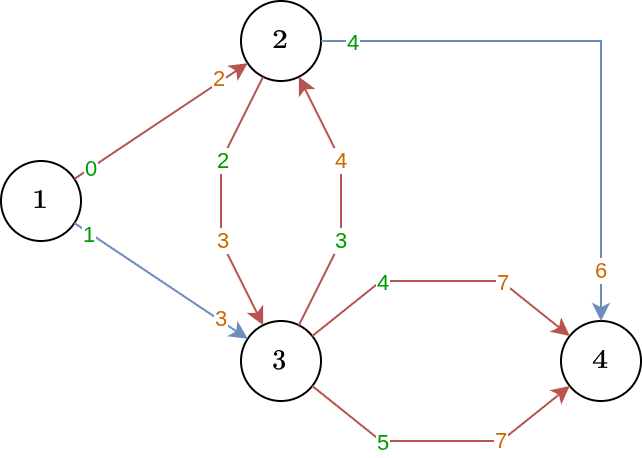
Minh họa cho ví dụ thứ ba
Tahp là một cậu bé say mê vẻ đẹp của những dãy núi hùng vĩ. Một ngày nọ, trong khi chơi với dãy số yêu thích của mình, cậu bỗng nảy ra một ý tưởng thú vị về cách sắp xếp các phần tử trong dãy để tạo thành hình dạng của một ngọn núi.
Giả sử dãy yêu thích của Tahp là ~a~ có độ dài ~n~. Cậu gọi ~a~ là một dãy núi nếu tồn tại một số nguyên ~k~ thỏa mãn tất cả các điều kiện sau:
~1 \le k \le n~
~a_i \le a_{i+1}~ cho tất cả ~1 \le i < k~
~a_i \le a_{i-1}~ cho tất cả ~k < i \le n~
Nói cách khác, dãy sẽ không giảm từ vị trí ~1~ đến ~k~, và sau đó sẽ không tăng từ vị trí ~k~ đến ~n~, giống như hình dạng của một ngọn núi.
Rõ ràng không phải mọi dãy đều là một dãy núi, vì vậy Tahp cần hoán đổi hai phần tử liên tiếp trong dãy đã cho nhiều lần để biến nó thành một dãy núi. Cậu định nghĩa độ chênh vênh của một dãy là số lần hoán đổi liên tiếp tối thiểu cần thiết để biến dãy đó thành một dãy núi.
Tahp ghi lại tất cả các hoán vị khác nhau~^*~ của dãy ~a~, và sau đó chọn hai dãy đặc biệt ~l~ và ~h~. Bây giờ, cậu muốn tính tổng độ chênh vênh của tất cả các hoán vị khác nhau ~p~ của ~a~ thỏa mãn ~l \le p \le h~ theo thứ tự từ điển~^\dagger~.
Nhiệm vụ của bạn là giúp Tahp tính tổng độ chênh vênh của tất cả các hoán vị khác nhau thỏa mãn điều kiện trên. Vì kết quả có thể rất lớn, bạn chỉ cần in phần dư sau khi chia đáp án cho ~998\,244\,353~.
—————————————
~^*~ Một hoán vị của một dãy là một dãy khác có cùng tập hợp các phần tử (bao gồm cả các phần tử trùng lặp, nếu có), nhưng có thể được sắp xếp theo bất kỳ thứ tự nào. Ví dụ, ~[1, 2, 2, 3]~, ~[2, 3, 1, 2]~, và ~[2, 2, 1, 3]~ là một số hoán vị của ~[3, 2, 1, 2]~, nhưng ~[2, 4, 3, 1]~, ~[2, 1, 2]~, và ~[1, 1, 2, 3]~ thì không. Hai hoán vị được coi là khác nhau nếu tồn tại một vị trí mà giá trị của phần tử trong hoán vị này khác với giá trị của phần tử ở cùng vị trí trong hoán vị còn lại.
~^\dagger~ Cho hai dãy số nguyên ~a = [a_1, a_2, \ldots, a_n]~ và ~b = [b_1, b_2, \ldots, b_n]~. Ta nói rằng ~a~ là nhỏ hơn hoặc bằng ~b~ theo thứ tự từ điển (ký hiệu ~a \le b~) nếu ~a_i = b_i~ cho tất cả ~1 \le i \le n~, hoặc nếu ~a_j < b_j~ với ~j~ là chỉ số nhỏ nhất thỏa mãn ~a_j \neq b_j~.
Input
Dòng đầu tiên chứa một số nguyên ~t~ (~1 \le t \le 10~) — số lượng test case. Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa một số nguyên duy nhất ~n~ (~1 \le n \le 1000~) — độ dài của dãy yêu thích của Tahp.
Dòng thứ hai chứa ~n~ số nguyên ~a_1, a_2, \dots, a_n~ (~1 \le a_i \le n~) — dãy yêu thích của Tahp.
Dòng thứ ba chứa ~n~ số nguyên ~l_1, l_2, \dots, l_n~ (~1 \le l_i \le n~) — dãy được chọn ~l~.
Dòng cuối cùng chứa ~n~ số nguyên ~h_1, h_2, \dots, h_n~ (~1 \le h_i \le n~) — dãy được chọn ~h~.
Đảm bảo rằng ~l~ và ~r~ là hai hoán vị của ~a~, và ~l \le h~ theo thứ tự từ điển.
Output
In ra ~t~ dòng, trong đó dòng thứ ~i~ chứa một số nguyên duy nhất là kết quả cho test case thứ ~i~ sau khi chia lấy phần dư cho ~998\,244\,353~.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~750~ | ~l_i = h_i~ với mọi ~1 \le i \le n~ |
| 2 | ~1250~ | ~n \le 200~ |
| 3 | ~1000~ | ~a~ là hoán vị của dãy ~1, 2, \ldots, n~ |
| 4 | ~1000~ | Không có ràng buộc gì thêm |
| Tổng | ~4000~ |
Sample Input 1
2
4
1 2 2 3
2 1 3 2
3 2 1 2
5
1 3 2 4 5
2 1 5 3 4
5 2 4 1 3
Sample Output 1
5
146
Notes
Trong test case đầu tiên, có ~7~ hoán vị khác nhau thỏa mãn như sau:
~[2, 1, 3, 2]~ có độ chênh vênh là ~1~: ~[\underline{2, 1}, 3, 2] \rightarrow [1, 2, \hat{3}, 2]~
~[2, 2, 1, 3]~ có độ chênh vênh là ~1~: ~[2, 2, \underline{1, 3}] \rightarrow [2, 2, \hat{3}, 1]~
~[2, 2, 3, 1]~ có độ chênh vênh là ~0~: ~[2, 2, \hat{3}, 1]~
~[2, 3, 1, 2]~ có độ chênh vênh là ~1~: ~[2, 3, \underline{1, 2}] \rightarrow [2, \hat{3}, 2, 1]~
~[2, 3, 2, 1]~ có độ chênh vênh là ~0~: ~[2, \hat{3}, 2, 1]~
~[3, 1, 2, 2]~ có độ chênh vênh là ~1~: ~[\underline{3, 1}, 2, 2] \rightarrow [1, \hat{3}, 2 , 2]~
~[3, 2, 1, 2]~ có độ chênh vênh là ~1~: ~[3, 2, \underline{1, 2}] \rightarrow [\hat{3}, 2, 2, 1]~
Tổng độ chênh vênh là ~1 + 1 + 0 + 1 + 0 + 1 + 1 = 5~.