[Mirror] VNOI CUP 2024 - Qualification Round 1
Có ~n~ thanh tre có độ dài ~a_1, a_2, \ldots, a_n~ nguyên dương. Bạn được phép thực hiện thao tác sau không hoặc nhiều lần:
- Chọn một thanh tre bất kì, bẻ thanh tre đó thành hai thanh tre nhỏ hơn có độ dài nguyên dương, sao cho hai thanh tre mới có độ dài không bằng nhau.
Sau khi thực hiện thao tác, bạn sử dụng những thanh tre để gom thành các đôi đũa. Một đôi đũa được tạo thành từ hai thanh tre có độ dài bằng nhau. Hãy tìm số lượng đôi đũa lớn nhất có thể tạo được sau khi thực hiện thao tác trên.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên chứa số lượng test case ~t~ (~1 \le t \le 10\,000~). Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa số nguyên ~n~ (~1 \le n \le 2 \cdot 10^5~) — số lượng thanh tre.
Dòng thứ hai chứa ~n~ số nguyên ~a_1, a_2, \ldots, a_n~ (~1 \le a_i \le 10^9~) — độ dài của các thanh tre.
Dữ liệu đảm bảo rằng tổng ~n~ trong tất cả các test case không quá ~2 \cdot 10^5~.
Output
Với mỗi test case, in ra một số nguyên duy nhất là số lượng đôi đũa lớn nhất tạo được.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~250~ | ~a_i \le 3~ |
| 2 | ~250~ | Không có ràng buộc gì thêm |
| Tổng | ~500~ |
Sample Input 1
2
7
1 1 1 2 2 2 2
4
2 3 3 2
Sample Output 1
3
3
Sample Input 2
2
1
4
10
3 1 4 1 5 9 2 6 5 3
Sample Output 2
1
15
Notes
Trong test case đầu tiên ở ví dụ đầu tiên, ta có ~3~ thanh tre độ dài ~1~, và ~4~ thanh tre độ dài ~2~. Ta không thể bẻ thanh tre nào thành hai thanh tre nhỏ hơn mà có độ dài khác nhau. Từ các thanh tre này, ta có thể tạo ra ~1~ đôi đũa từ hai thanh tre độ dài ~1~, và thêm ~2~ đôi đũa nữa từ các thanh tre độ dài ~2~. Như vậy số lượng đôi đũa có thể tạo được là ~1 + 2 = 3~.
Lưu ý ta còn lại một thanh tre độ dài ~1~ không ghép với thanh tre nào cả.
Trong test case thứ hai ở ví dụ đầu tiên, ta có thể bẻ thanh tre có độ dài ~3~ thành hai thanh tre nhỏ hơn có độ dài ~1~ và ~2~. Như vậy ta sẽ có ~1~ đôi đũa từ thanh tre độ dài ~1~, và ~2~ đôi đũa từ thanh tre độ dài ~2~. Như vậy ta cũng vẫn thu được ~1 + 2 = 3~ đôi đũa.
Trong test case đầu tiên ở ví dụ thứ hai, ta có duy nhất một thanh tre độ dài ~4~. Ban đầu ta có thể bẻ thanh tre này thành thanh tre độ dài ~1~ và ~3~. Tiếp đó ta có thể bẻ thanh tre độ dài ~3~ thành thanh tre độ dài ~1~ và ~2~. Từ đây ta có thể tạo ra một đôi đũa từ hai thanh tre độ dài ~1~.
Bạn đang chơi trò chơi MMO thịnh hành nhất hiện tại. Hệ thống tiền tệ của game là ngọc, được chia làm ~n~ cấp độ. Hiện tại, bạn đang có ~a_i~ viên ngọc ở cấp độ ~i~. Để mua món trang bị đắt tiền nhất trong game hiện giờ, bạn cần trả ~b_i~ viên ngọc ở cấp độ ~i~.
Trò chơi có hệ thống đổi ngọc, cho phép bạn:
Đổi ~2~ viên ngọc ở cấp độ ~i~ để lấy ~1~ viên ngọc ở cấp độ ~i+1~ (với ~1 \le i < n~).
Đổi ~1~ viên ngọc ở cấp độ ~i~ để lấy ~2~ viên ngọc ở cấp độ ~i-1~ (với ~1 < i \le n~).
Hãy cho biết có cách đổi ngọc nào giúp bạn có đủ số ngọc cần có ở mỗi cấp độ để mua trang bị bằng cách đổi ngọc không hay nhiều lần hay không.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên của bộ dữ liệu chứa số nguyên dương ~t~ (~1 \le t \le 10\,000~) là số lượng test case. Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa số nguyên ~n~ (~1 \le n \le 2 \cdot 10^5~) — số lượng cấp độ ngọc.
Dòng thứ hai chứa ~n~ số nguyên ~a_1, a_2, \ldots, a_n~ (~0 \le a_i \le 10^9~) — số viên ngọc bạn đang có ở mỗi cấp độ.
Dòng thứ ba chứa ~n~ số nguyên ~b_1, b_2, \ldots, b_n~ (~0 \le b_i \le 10^9~) — số viên ngọc cần có ở mỗi cấp độ.
Dữ liệu đảm bảo rằng tổng ~n~ trong tất cả các test case không quá ~2 \cdot 10^5~.
Output
Với mỗi test case, hãy in ra "YES" nếu tồn tại cách đổi ngọc để đạt đủ số ngọc cần có ở mỗi cấp độ, hoặc in ra "NO" trong trường hợp ngược lại.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~500~ | ~n \le 20~ |
| 2 | ~500~ | Không có ràng buộc gì thêm |
| Tổng | ~1000~ |
Sample Input 1
4
4
1 1 4 5
3 1 2 3
2
1 0
0 1
3
1 1 1
1 1 1
1
1
100
Sample Output 1
YES
NO
YES
NO
Notes
Trong test case đầu tiên, bạn có thể:
Đổi ~1~ viên ngọc cấp ~2~ để lấy ~2~ viên ngọc cấp ~1~. Số ngọc bạn có ở từng cấp độ trở thành ~[3, 0, 4, 5]~.
Đổi ~1~ viên ngọc cấp ~3~ để lấy ~2~ viên ngọc cấp ~2~. Số ngọc bạn có ở từng cấp độ trở thành ~[3, 2, 3, 5]~.
Lúc này, bạn đã có đủ số lượng ngọc cần có ở mỗi cấp độ.
Trong test case thứ hai, bạn chỉ có ~1~ viên ngọc cấp ~1~, nên bạn không thể thực hiện bất kì phép đổi ngọc nào. Do đó, bạn không thể có đủ lượng ngọc cấp ~2~ được yêu cầu.
Trong test case thứ ba, ngay từ đầu bạn đã có đủ số ngọc cần có ở mỗi cấp độ.
Trong test case thứ tư, hệ thống chỉ có đúng ~1~ cấp độ ngọc nên bạn không thể thực hiện bất kì phép đổi ngọc nào, đồng thời bạn cũng không có đủ lượng ngọc cấp ~1~ được yêu cầu.
Cho số nguyên không âm ~x~, hãy tìm dãy số nguyên ~a_1, a_2, \ldots, a_n~ thỏa mãn các điều kiện sau:
~0 \le a_i \le x~ với ~1 \le i \le n~.
Tổng AND của các dãy con liên tiếp của ~a~ là đôi một phân biệt.
Nói cách khác, định nghĩa ~f(l, r)=a_l \,\&\, a_{l+1} \,\&\, \ldots \,\&\, a_r~ (tổng AND của dãy con liên tiếp từ vị trí ~l~ đến vị trí ~r~). Với mọi bộ bốn chỉ số ~(l_1, r_1, l_2, r_2)~ sao cho ~l_1 \le r_1~, ~l_2 \le r_2~ và ~(l_1, r_1) \ne (l_2, r_2)~ thì ~f(l_1, r_1) \ne f(l_2, r_2)~.
Độ dài ~n~ là lớn nhất có thể.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên của bộ dữ liệu chứa số nguyên dương ~t~ (~1 \le t \le 10~) là số lượng test case. Mô tả của mỗi test case như sau.
Mỗi test case gồm một số nguyên duy nhất ~x~ (~1 \le x \le 10^6~) — giới hạn giá trị của dãy ~a~.
Output
Với mỗi test case, hãy in ra đáp án theo định dạng như sau:
Dòng đầu tiên gồm số nguyên ~n~ (~1 \le n \le 2000~) — độ dài dãy ~a~.
Dòng thứ hai gồm ~n~ số nguyên ~a_1, a_2, \ldots, a_n~ (~0 \le a_i \le x~) — các phần tử của dãy ~a~.
Có thể chỉ ra rằng độ dài dãy ~a~ thỏa yêu cầu đề bài không thể vượt quá ~2000~.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~500~ | ~x \le 16~ |
| 2 | ~1250~ | Không có ràng buộc gì thêm |
| Tổng | ~1750~ |
Sample Input 1
2
1
2
Sample Output 1
1
1
2
1 2
Notes
Ở test case thứ hai, với ~a = [1, 2]~ thì:
Đoạn con ~[1]~ có giá trị tổng AND bằng ~1~.
Đoạn con ~[2]~ có giá trị tổng AND bằng ~2~.
Đoạn con ~[1, 2]~ có giá trị tổng AND bằng ~1 \,\&\, 2 = 0~.
Cả ba đoạn con đều có giá trị tổng AND phân biệt nhau, nên dãy ~a~ thỏa yêu cầu đề bài. Có thể chứng minh không tồn tại dãy ~a~ có độ dài từ ~3~ trở lên thỏa yêu cầu đề bài.
Cho ~n~ nam châm trên trục tọa độ ~Ox~, nam châm thứ ~i~ có tọa độ ~x_i~. Các nam châm được đánh số từ ~1~ đến ~n~ theo tọa độ tăng dần, đồng thời có kích thước không đáng kể. Bạn có thể thực hiện phép toán sau với số lần tùy ý:
Chọn hai nam châm ~i~ và ~j~ (~i < j~) và số thực ~t~.
Kích hoạt hai nam châm ~i~ và ~j~ với tham số ~t~. Khi đó, nam châm ~i~ sẽ di chuyển đến tọa độ ~x_i + t~, nam châm ~j~ sẽ di chuyển đến tọa độ ~x_j - t~.
Các nam châm không được phép vượt mặt nhau trong quá trình di chuyển. Nói cách khác, ~t \le \min\left(\frac{x_j - x_i}{2}, x_{i+1} - x_i, x_j - x_{j-1}\right)~.
Bạn sẽ nhận được điểm số ~t~.
Hãy tìm tổng điểm số tối đa có thể nhận được sau khi thực hiện phép toán trên.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên của bộ dữ liệu chứa số nguyên dương ~t~ (~1 \le t \le 100~) là số lượng test case. Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa số nguyên ~n~ (~2 \le n \le 2 \cdot 10^5~) — số lượng nam châm.
Dòng thứ hai chứa ~n~ số nguyên ~x_1, x_2, \ldots, x_n~ (~0 \le x_1 < x_2 < \ldots < x_n \le 10^6~) — tọa độ của các viên nam châm.
Dữ liệu đảm bảo tổng ~n~ trong tất cả các test case không quá ~2 \cdot 10^5~.
Output
Với mỗi test case, in ra một số thực duy nhất là tổng điểm lớn nhất có thể nhận được.
Định nghĩa ~J~ là đáp án của ban tổ chức, ~P~ là đáp án mà bạn đưa ra. Đáp án của bạn sẽ được cho là đúng nếu như sai số tương đối hoặc tuyệt đối so với đáp án của ban tổ chức không vượt quá ~10^{-6}~, hay ~\displaystyle\frac{|P - J|}{\max\{1, |J|\}} \le 10^{-6}~.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~1000~ | ~n \le 100~ |
| 2 | ~1250~ | Không có ràng buộc gì thêm |
| Tổng | ~2250~ |
Sample Input 1
2
2
1 4
3
0 1 2
Sample Output 1
1.5
2
Notes
Ở ví dụ thứ nhất, ta sẽ chọn hai nam châm ở tọa độ ~1~ và ~4~ với ~t = 1.5~. Tọa độ sau khi thực hiện phép toán là ~[2.5, 2.5]~. Ta không thực hiện được thêm phép toán nào khác, nên tổng điểm số lớn nhất là ~1.5~.
Ở ví dụ thứ hai, ta sẽ thực hiện phép toán như sau:
Chọn hai nam châm ở tọa độ ~0~ và ~1~ và ~t = 0.5~. Tọa độ sau khi thực hiện phép toán là ~[0.5, 0.5, 2]~
Chọn hai nam châm ở tọa độ ~0.5~ và ~2~ với ~t = 0.5~. Tọa độ sau khi thực hiện phép toán là ~[0.5, 1, 1.5]~
Chọn hai nam châm ở tọa độ ~0.5~ và ~1~ với ~t = 0.25~. Tọa độ sau khi thực hiện phép toán là ~[0.75, 0.75, 1.5]~
Chọn hai nam châm ở tọa độ ~0.75~ và ~1.5~ với ~t = 0.25~. Tọa độ sau khi thực hiện phép toán là ~[0.75, 1, 1.25]~
...
Tổng điểm số là ~0.5 + 0.5 + 0.25 + 0.25 + ... = 2 \times \sum_{x=1}^{\infty} \left( \frac{1}{2} \right)^x = 2~.
Trên hệ tọa độ 2 chiều, ta kẻ ~n~ đường zigzag, với đường zigzag thứ ~i~ bắt đầu từ điểm ~(x_i, y_i)~, có độ dài là ~l_i~, và thuộc một trong hai loại:
Loại ~0~: Xuất phát từ ~(x_i, y_i)~, ta nối các điểm ~(x_i, y_i) \to (x_i + 1, y_i) \to (x_i + 1, y_i + 1) \to (x_i + 2, y_i + 1) \to (x_i + 2, y_i + 2) \to \dots \to (x_i+\left\lceil\frac{l_i}{2}\right\rceil, y_i+\left\lfloor\frac{l_i}{2}\right\rfloor)~.
Loại ~1~: Xuất phát từ ~(x_i, y_i)~, ta nối các điểm ~(x_i, y_i) \to (x_i, y_i + 1) \to (x_i + 1, y_i + 1) \to (x_i + 1, y_i + 2) \to (x_i + 2, y_i + 2) \to \dots \to \left(x_i+\left\lfloor\frac{l_i}{2}\right\rfloor, y_i+\left\lceil\frac{l_i}{2}\right\rceil\right)~.
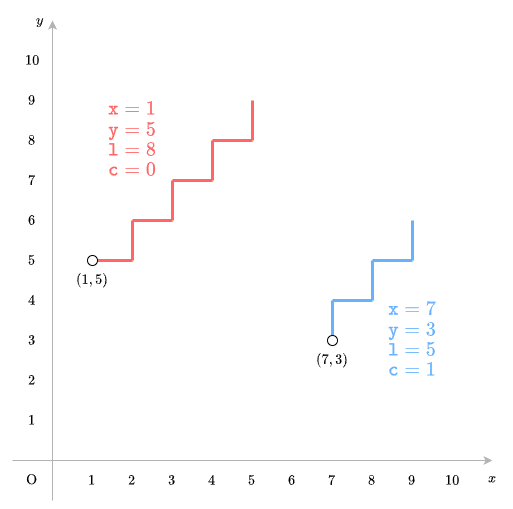
Đường màu đỏ là đường zigzag loại ~0~, bắt đầu từ điểm ~(1, 5)~ với độ dài ~8~. Đường màu xanh là đường zigzag loại ~1~, bắt đầu từ điểm ~(7, 3)~ với độ dài ~5~.
Định nghĩa ~f(i, j)~ là số điểm nguyên chung của đường zigzag thứ ~i~ và đường zigzag thứ ~j~. Hãy tính ~\sum_{i = 1}^n \sum_{j=i+1}^n f(i, j)~.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên chứa số lượng test case ~t~ (~1 \le t \le 10\,000~). Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa một số nguyên ~n~ (~1 \le n \le 2 \cdot 10^5~) — số lượng đường zigzag.
Dòng thứ ~i~ trong ~n~ dòng tiếp theo chứa bốn số nguyên ~x_{i}, y_{i}, l_i, c_i~ (~0 \le x_i, y_i \le 10^6~, ~2 \le l_i \le 10^6~, ~0 \le c_i \le 1~) — đường zigzag thứ ~i~ bắt đầu từ điểm ~(x_i, y_i)~, có độ dài là ~l_i~, và thuộc loại ~c_i~.
Dữ liệu đảm bảo rằng tổng ~n~ trong tất cả các test case không vượt quá ~2 \cdot 10^5~.
Output
Với mỗi test case, in ra một số nguyên là đáp án của bài toán.
Scoring
Với mỗi test case, định nghĩa ~X = \max(\max x, \max y, \max l)~.
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~500~ | ~n = 2~ |
| 2 | ~750~ | ~\sum X \le 2500~ |
| 3 | ~750~ | Trong một test, ~c_i = 0~ hoặc ~c_i = 1~ với mọi ~i~ |
| 4 | ~500~ | Không có ràng buộc gì thêm |
| Tổng | ~2500~ |
Sample Input 1
2
2
0 0 3 0
0 1 3 0
3
2 3 5 0
2 3 8 1
3 3 3 0
Sample Output 1
1
5
Sample Input 2
2
5
10 10 2 0
9 9 10 1
0 0 20 0
0 0 30 0
1 1 40 0
3
15 20 12 0
20 15 34 0
10 10 56 1
Sample Output 2
92
0
Notes
Dưới đây là minh họa cho test case đầu tiên của ví dụ đầu tiên.
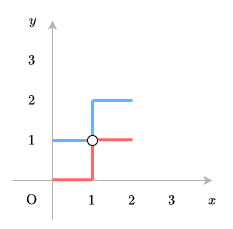
Đường màu đỏ và đường màu xanh lần lượt là đường zigzag thứ nhất và thứ hai trong đầu vào. Chúng giao nhau tại điểm chấm, được hiển thị trong minh họa.
Dưới đây là minh họa cho test case thứ hai của ví dụ đầu tiên.
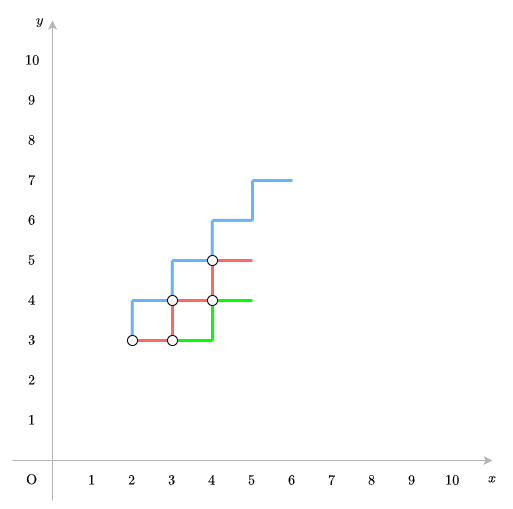
Đường màu đỏ, xanh nước biển và xanh lá cây lần lượt là đường zigzag thứ nhất, thứ hai và thứ ba trong đầu vào. Đường màu xanh nước biển và đường màu đỏ có ~3~ điểm nguyên chung, trong khi đường màu đỏ và đường màu xanh lá cây có ~2~ điểm nguyên chung.
Điểm: 3250
Cho số nguyên ~k~ và xâu ~s~ có độ dài ~n~. Tưởng tượng bạn viết xuống toàn bộ ~2^n - 1~ dãy con không rỗng~^\dagger~ của xâu ~s~. Hãy đếm số lượng xâu ~t~ khác nhau được viết xuống đúng ~k~ lần. Vì kết quả có thể rất lớn, bạn cần tính theo modulo ~998\,244\,353~.
~^\dagger~ Một xâu ~t~ là một dãy con của xâu ~s~ nếu ~t~ có thể được thu được từ ~s~ bằng cách xóa đi một số (có thể là không) ký tự.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên chứa số lượng test case ~t~ (~1 \leq t \leq 10\,000~), theo sau là số lần xuất hiện dự định ~k~ (~1 \leq k \leq 2~), giống nhau cho mọi test case. Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa một số nguyên ~n~ (~1 \le n \le 3 \cdot 10^5~) — độ dài của xâu ~s~.
Dòng thứ hai chứa xâu ~s~ gồm ~n~ ký tự Latinh in thường.
Đảm bảo rằng tổng của ~n~ qua tất cả các test case không vượt quá ~3 \cdot 10^5~.
Output
Với mỗi test case, in ra một số nguyên là số lượng xâu xuất hiện chính xác ~k~ lần như một dãy con trong ~s~, theo modulo ~998\,244\,353~.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~500~ | Tổng của ~n~ qua tất cả các test case không vượt quá ~20~ |
| 2 | ~1000~ | ~k = 1~ |
| 3 | ~1750~ | ~k = 2~ |
| Tổng | ~3250~ |
Sample Input 1
3 2
3
aab
10
vnoihaibon
35
hiiamcurrentlyafirstyearphdstudents
Sample Output 1
2
74
911464594
Sample Input 2
3 1
3
aab
7
vnoicup
38
asomewhatnotshortblogonflowwithdemands
Sample Output 2
3
127
395878133
Notes
Test case đầu tiên của cả hai ví dụ có ~s = \mathtt{aab}~. Toàn bộ các dãy con không rỗng của ~s~ là ~[\mathtt{a}, \mathtt{a}, \mathtt{b}, \mathtt{aa}, \mathtt{ab}, \mathtt{ab}, \mathtt{aab}]~. Ta có thể thấy ~\mathtt{b}~, ~\mathtt{aa}~, và ~\mathtt{aab}~ xuất hiện một lần, còn ~\mathtt{a}~ và ~\mathtt{ab}~ xuất hiện hai lần.
Điểm: 4000
Cho một đa tập ~S~ gồm ~n~ số nguyên không âm. Hãy thực hiện ~q~ truy vấn thuộc một trong ba dạng sau:
~\mathtt{1\;} x~: Thêm ~x~ vào ~S~.
~\mathtt{2\;} x~: Xóa một lần xuất hiện của ~x~ khỏi ~S~.
~\mathtt{3\;} k~: Trong các cách chia ~S~ thành ~k~ đa tập con không rỗng ~S_1,S_2,\ldots, S_k~, hãy tìm cách chia có tổng ~\displaystyle \sum_{i=1}^k \operatorname{cost}(S_i)~ là lớn nhất. Ở đây, với ~X=\{x_1, x_2, \ldots, x_q\}~, định nghĩa ~\operatorname{cost}(X)=x_1\,\&\,x_2\,\&\,\ldots\,\&\,x_q~ với ~\&~ là toán tử AND.
Input
Dòng đầu tiên gồm hai số nguyên ~n~ và ~q~ (~1\le n, q\le 10^5~) — số phần tử của ~S~ và số lượng truy vấn.
Dòng thứ hai gồm ~n~ số nguyên ~s_1,s_2,\ldots,s_n~ (~0\le s_i<2^{30}~) — các phần tử của ~S~.
Mỗi dòng trong ~q~ dòng tiếp theo gồm hai số nguyên mô tả các truy vấn. Số nguyên đầu tiên là ~t~ sẽ nhận giá trị thuộc ~\{1,2,3\}~.
Nếu ~t=1~, tiếp theo là một số nguyên ~x~ (~0\le x<2^{30}~) — số nguyên cần thêm vào ~S~.
Nếu ~t=2~, tiếp theo là một số nguyên ~x~ (~0\le x<2^{30}~; ~x \in S~) — số nguyên cần xóa khỏi ~S~.
Nếu ~t=3~, tiếp theo là một số nguyên ~k~ (~1\le k\le |S|~) — số đa tập con cần chia ra.
Output
Với mỗi truy vấn loại ~3~, in ra một số nguyên là kết quả của truy vấn trên một dòng.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~1000~ | ~n, q\le 2000~; có tất cả ~q = n~ truy vấn, trong đó truy vấn thứ ~i~ là "~\mathtt{3\;} i~" |
| 2 | ~750~ | Có tất cả ~q = n~ truy vấn, trong đó truy vấn thứ ~i~ là "~\mathtt{3\;} i~" |
| 3 | ~1000~ | ~n, q\le 2000~ |
| 4 | ~1250~ | Không có ràng buộc gì thêm |
| Tổng | ~4000~ |
Sample Input 1
3 5
3 4 5
3 2
1 4
3 3
2 5
3 2
Sample Output 1
7
12
7
Sample Input 2
6 6
5 5 6 6 7 7
3 1
3 2
3 3
3 4
3 5
3 6
Sample Output 2
4
11
18
25
31
36
Notes
Đối với ví dụ đầu tiên, đa tập hợp ban đầu là ~\{3, 4, 5\}~:
Một cách chia tối ưu cho ~k=2~ là ~\{3\}, \{4, 5\}~.
Đa tập hợp mới sau khi thêm ~4~ là ~\{3, 4, 4, 5\}~.
Một cách chia tối ưu cho ~k=3~ là ~\{3\}, \{4, 4\}, \{5\}~.
Đa tập hợp mới sau khi xóa ~5~ là ~\{3, 4, 4\}~.
Một cách chia tối ưu cho ~k=2~ là ~\{3\}, \{4, 4\}~.