[Mirror] VNOI Cup 2022 - Round 3
Điểm: 50
To read the problem statement in English, choose the language using the flag on the navigation bar.
Cờ vua là một loại trò chơi cờ với hai người chơi, và cũng là loại cờ nổi tiếng nhât thế giới. Bé Mèo rất muốn học chơi cờ, nhưng trong cờ vua có đến ~6~ loại quân khác nhau, mỗi loại lại có một cách di chuyển khác nhau, nên Bé Mèo cảm thấy rất bối rối! Vì vậy hôm nay chúng ta giúp Bé Mèo làm quen với quân tượng, nhưng với một bàn cờ vua có kích thước là ~n \times n~ bất kì.
Một bàn cơ vua có kích thước ~n \times n~ là bàn cờ vua gồm có ~n~ hàng và ~n~ cột. Các hàng được đánh số từ ~1~ đến ~n~ từ trên xuống, và các cột được đánh số từ ~1~ đến ~n~ từ trái qua phải. Ô ở hàng thứ ~r~ và cột thứ ~c~ được biểu diễn bởi cặp số ~(r, c)~.
Ta có thể di chuyển quân tượng theo đường chéo trên bàn cờ. Cụ thể, nếu như có một quân tượng tại vị trí ~(i, j)~, ta có thể di chuyển quân tượng đến ô ~(i', j')~ thỏa mãn ~|i - i'| = |j - j'|~.
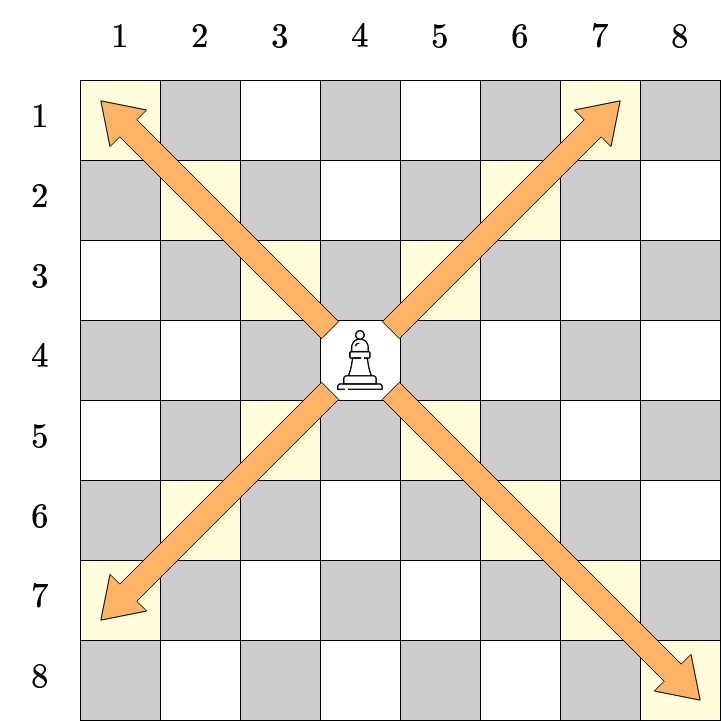
Minh họa cho các nước đi của quân tượng tại vị trí ~(4, 4)~. Các ô màu vàng là các ô mà quân tượng này có thể đến được
Để làm quen với cách di chuyển quân tượng, Bé Mèo cần thực hiện bài tập sau. Trên bàn cờ của chúng ta hiện tại có duy nhất một quân tượng tại vị trí ~(i, j)~. Hãy kiểm tra xem ta có thể di chuyển quân tượng đến ô ~(x, y)~ bằng một vài nước di chuyển (có thê không cần di chuyển) hay không. Nếu có thể, hãy tìm một cách đi từ ô ~(i, j)~ đến ô ~(x, y))~ với số lượng nước di chuyển cần thực hiện là ít nhất có thể. Để thành thạo, nên Bé Mèo cần luyện tập bài tập này ~q~ lần. Nhưng Bé Mèo vẫn đang rất mải chơi, nên không chịu tập chung luyện tập, nên bạn hãy giúp Bé Mèo thực hiện bài tập này nhé!
Input
Dòng đầu tiên chứa hai số nguyên ~n~ và ~q~ (~1 \le n \le 10^9~, ~1 \le q \le 10^5~) lần lượt là số hàng của bàn cờ vua, số cột của bàn cờ vua, và số lượng bài tập bạn cần thực hiện.
Mỗi dòng trong ~q~ dòng tiếp theo, mỗi dòng chứa bốn số nguyên ~i~, ~j~, ~x~ và ~y~ (~1 \le i, j, x, y \le n~), với ~(i, j)~ thể hiện vị trí của quân tượng, và ~(x, y)~ là vị trí cần di chuyển quân tượng đến trong bài tập.
Output
Với mỗi bài tập, nếu không có cách nào di chuyển quân tượng từ ô ~(i, j)~ đến ô ~(x, y)~, hãy in ra ~-1~.
Ngược lại, hãy in ra số ~s~ là số lượng nước di chuyển ít nhất cần thực hiện để di chuyển quân tượng từ. Sau đó, hãy in ra ~s~ dòng. Trên dòng thứ ~t~, hãy in ra hai số nguyên ~r~ và ~c~ là ô cần di chuyển tới trong nước di chuyển thứ ~t~.
Nếu có nhiều cách di chuyển quân tượng đến đích, hãy in ra cách di chuyển bất kì.
Scoring
Subtask 1, tương ứng với ~15~ điểm, có ~n \le 2~.
Subtask 2, tương ứng với ~15~ điểm, có ~n \le 8~.
Subtask 3, tương ứng với ~20~ điểm, không có ràng buộc gì thêm.
Tổng cộng bài toán có ~50~ điểm.
Sample Input 1
2 4
1 1 1 1
1 1 2 2
2 1 2 2
1 2 2 1
Sample Output 1
0
1
2 2
-1
1
2 1
Sample Input 2
3 5
1 1 3 3
2 1 2 3
1 2 3 2
2 2 1 1
2 2 1 2
Sample Output 2
1
3 3
2
1 2
2 3
2
2 1
3 2
1
1 1
-1
Notes
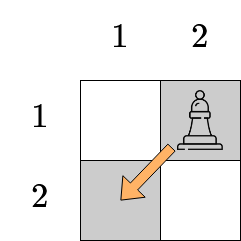
Trong bài tập cuối của ở ví dụ đầu tiên, Bé Mèo có thể di chuyển quân tượng với một nước đi như sau:
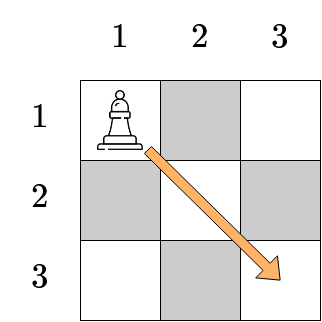
Trong bài tập đều tiên ở ví dụ thứ hai, Bé Mèo có thể di chuyển quân tượng trong một nước đi như sau:
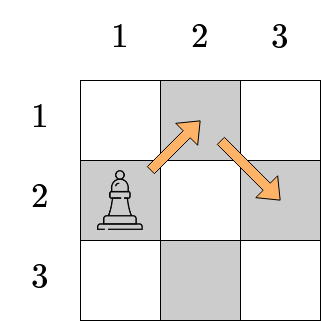
Trong bài tập thứ hai ở ví dụ thứ hai, Bé Mèo có thể di chuyển quân tượng trong hai nước đi như sau. Lưu ý rằng trong bài tập này cũng có thể di chuyển quân tượng đến ô ~(3, 2)~ trước rồi mới di chuyển quân tượng đến đích.
Điểm: 100
To read the problem statement in English, choose the language using the flag on the navigation bar.
Một xâu kí tự được gọi là chuỗi ngoặc nếu như trong xâu kí tự chỉ có kí
tự '(' hoặc ')'.
Một chuỗi ngoặc ~X~ được gọi là đơn giản nếu như:
hoặc ~X~ bằng "
()",hoặc ~X~ có dạng "
(Y)", với ~Y~ là một chuỗi ngoặc đơn giản.
Ví dụ, các chuỗi ngoặc (), (()) và (((()))) là các chuỗi ngoặc đơn
giản, trong khi ()(), )(, (())() hay (()()) thì không phải.
Xét một chuỗi ngoặc ~S~. Nếu như trong ~S~ tồn tại một xâu con là chuỗi ngoặc đơn giản, ta có thể thực hiện thao tác xóa chuỗi ngoặc đơn giản bất kì trong xâu ~S~ đi. Ta gọi độ phức tạp của một chuỗi ngoặc ~S~ là số lần thực hiện thao tác ít nhất cần thực hiện để xâu ~S~ không chứa xâu con nào là chuỗi ngoặc đơn giản.
Cho một chuỗi ngoặc ~P~ có độ dài ~n~ và ~q~ truy vấn, truy vấn thứ ~i~ sẽ có dạng ~(l_i, r_i)~, hãy tính độ phức tạp của xâu ~P_{l_i \ldots r_i}~, tức xâu kí tự tạo bởi các kí tự của xâu ~P~ từ vị trí ~l_i~ đến ~r_i~.
Một xâu kí tự ~a~ được gọi là xâu con của xâu kí tự ~b~, nếu như ~a~ có thể thu được bằng cách xóa từ ~b~ một vài kí tự ở đầu (có thể là không kí tự nào), và xóa đi một vài kí tự ở cuối (có thể là không kí tự nào).
Input
Dòng đầu tiên chứa hai số nguyên ~n~ và ~q~ (~1 \le n \le 10^5~, ~1 \le q \le 10^5~) lần lượt là độ dài xâu ~P~ và số lượng truy vấn cần trả lời.
Dòng tiếp theo chứa chuỗi ngoặc ~P~ có độ dài ~n~.
Dòng thứ ~i~ trong số ~q~ dòng tiếp theo chứa hai số nguyên ~l_i~ và ~r_i~ (~1 \le l_i \le r_i \le n~), thể hiện truy vấn thứ ~i~ của bài toán.
Output
In ra ~q~ dòng, dòng thứ ~i~ là độ phức tạp của xâu con ~P_{l_i \ldots r_i}~.
Scoring
Subtask 1, tương ứng với ~40~ điểm, có ~n, q \le 1000~.
Subtask 2, tương ứng với ~60~ điểm, không có ràng buộc gì thêm.
Tổng cộng bài toán sẽ có ~100~ điểm.
Sample Input 1
8 3
(()))(()
1 8
1 5
2 8
Sample Output 1
2
1
2
Notes
Ở truy vấn đầu tiên, xâu con ta cần tìm độ phức tạp là xâu
~P_{1\ldots 8}~ hay "(()))(()". Ta có thể thực hiện các thao tác biến
đổi sau (xóa các kí tự bị gạch ngang):
(()))( ~\rightarrow~ ()(()))()(
Có thể thấy đây là một cách xóa tối ưu, và ~2~ thao tác là số thao tác ít nhất cần thực hiện.
Điểm: 150
To read the problem statement in English, choose the language using the flag on the navigation bar.
Trong nông trại của bác nông dân John có ~m~ cây táo. Hiện tại cũng đã đến mùa thu hoạch táo. Trước đây lực lượng lao động chính trong việc thu hoạch táo trong nông trại của bác nông dân John chính là bò Bessie và bạn của cô. Nhưng John cũng nhận thấy rằng sử dụng bò để thu hoạch táo có chi phí rất cao (chi phí nuôi bò là không thấp), nhưng lượng táo thu về có phần hao hụt (những chú bò đã ăn vụng táo??!?).
Để giảm chi phí trong công đoạn thu hoạch, cũng như gia tăng tự động hóa cho nông trại, bác nông dân John quyết định đầu tư chi phí để mua ~n~ con robot, được đánh số từ ~1~ đến ~n~. Những con robot mà bác nông dân John sẽ mua đều rất linh hoạt trong quá trình hái táo, cũng như di chuyển táo về kho. Chỉ có một tham số duy nhất của những con robot ảnh hưởng đến quá trình thu hoạch, đó chính là độ cao: chỉ có những con robot có độ cao vừa tầm cây sẽ được sử dụng để hái táo, trong khi đó những con robot thấp hơn, nhưng vừa tầm, sẽ đứng phía dưới hứng táo và di chuyển táo về kho.
Trước khi mua robot, bác nông dân John đã lên kế hoạch hái táo cho từng cây. Với cây thứ ~i~ (~1 \le i \le m~), bác nông dân sẽ chọn hai con robot có số thứ tự là ~u_i~ và ~v_i~ (~1 \le u_i, v_i \le n~, ~u_i \ne v_i~). Bác muốn rằng con robot cao hơn cần có độ cao là ~y_i~ để hái táo, và con robot thấp hơn cần có độ cao là ~x_i~ để hứng và di chuyển táo về kho (~x_i \le y_i~). Đó là kế hoạch của bác nông dân John, tuy nhiên bác cũng chưa biết chính xác độ cao của từng con robot mà mình sẽ mua như thế nào.
Tuy bò Bessie sẽ không làm nhiệm vụ thu hoạch táo nữa, nhưng bây giờ bò Bessie sẽ giúp bác nông dân John làm nhiệm vụ mua các con robot này và bào trì chúng. Cho biết kế hoạch hái táo của bác John, hãy giúp bò Bessie tìm ra độ cao của ~n~ con robot cần mua thỏa mãn kế hoạch của bác nông dân John. Nếu như có nhiều đáp án thỏa mãn, hãy giúp bò Bessie tìm ra đáp án bất kì. Nếu như không có đáp án nào thỏa mãn cả, bạn cũng cần thông báo cho bò Bessie biết để bò Bessie thuyết phục lại bác nông dân trao lại công việc cũ cho mình.
Input
Dòng đầ tiên chứa hai số nguyên ~n~ và ~m~ (~2 \le n \le 10^5~, ~1 \le m \le 10^5~), lần lượt là số lượng robot mà bác nông dân John dự định mua, và số lượng cây táo trong nông trại.
Dòng thứ ~i~ trong ~m~ dòng tiếp theo chứa ~4~ số nguyên dương ~u_i~, ~v_i~, ~x_i~ và ~y_i~ (~1 \le u_i, v_i \le n~, ~u_i \ne v_i~, ~1 \le x_i \le y_i \le 10^9~) thể hiện kế hoạch hái táo cho cây thứ ~i~.
Output
Nếu không thể mua ~n~ con robot thỏa mãn kế hoạch của bác nông dân John, hãy in ra ~-1~.
Ngược lại, hãy in ra ~n~ số nguyên, số thứ ~i~ trong đó là độ cao của con robot thứ ~i~. Độ cao của mỗi con robot được in ra cần không dưới ~1~ và không quá ~10^9~. Nếu có nhiều đáp án, hãy in ra đáp án bất kì.
Scoring
Subtask 1, tương ứng với ~15~ điểm, có ~n = 2~ và ~m = 1~.
Subtask 2, tương ứng với ~30~ điểm, có ~n \le 6~.
Subtask 3, tương ứng với ~45~ điểm, có ~n \le 16~.
Subtask 4, tương ứng với ~60~, không có ràng buộc gì thêm.
Tổng cộng bài toán có ~150~ điểm.
Sample Input 1
2 1
1 2 3 4
Sample Output 1
3 4
Sample Input 2
6 3
1 3 2 3
3 5 1 3
5 1 1 2
Sample Output 2
2 2 3 3 1 1
Sample Input 3
3 2
1 2 1 1
2 3 2 2
Sample Output 3
-1
Notes
Để thuật tiện trong quá trình giải thích, ta gọi ~h_i~ là độ cao của con robot thứ ~i~.
Trong ví dụ đầu tiên, trong vườn có ~m = 1~ cây táo. Bác nông dân muốn rằng cây táo này sẽ được thu hoạch bởi con robot ~1~ và ~2~, trong đó con robot cao hơn cần có độ cao là ~4~ để hái táo, và con robot thấp hơn cần có độ cao là ~3~ để hứng táo và mang táo về kho. Vì vai trò của hai con robot là như nhau, nên ngoài cách mua robot với ~h_1 = 3~ và ~h_2 = 4~, ta cũng có cách mua khác là ~h_1 = 4~ và ~h_2 = 3~.
Trong ví dụ thứ hai, tuy bác nông dân John muốn mua ~n = 6~ con robot để thu hoạch ~m = 3~ cây táo, tuy nhiên chỉ có con robot ~1~, ~3~ và ~5~ được sử dụng và có duy nhất một cách mua thỏa mãn là ~h_1 = 2~, ~h_3 = 3~ và ~h_5 = 1~. Các con robot ~2~, ~4~ và ~6~ có thể có độ cao bất kì và có thể được sử dụng cho mục đích khác (ví dụ như thay thế các con robot kia trong trường hợp hỏng hóc).
Trong ví dụ thứ ba:
robot ~1~ và ~2~ được sử dụng để hai cây táo thứ nhất, và chúng cần có độ cao bằng nhau và bằng ~1~,
robot ~2~ và ~3~ được sử dụng để hai cây táo thứ hai, và chúng cần có độ cao bằng nhau và bằng ~2~.
Robot ~2~ không thể vừa có độ cao ~1~ và ~2~ được, nên không có cách mua robot nào thỏa mãn kế hoạch của bác nông dân John.
Điểm: 310
To read the problem statement in English, choose the language using the flag on the navigation bar.
Mỗi vị thần rừng đều quản lý một khu rừng. Mỗi khu rừng có ~n~ vị trí đánh số ~1~ đến ~n~, và mỗi vị trí có tối đa một cây.
Ai cũng biết một vị thần rừng có cấp bậc ~k~ có thể thực hiện hai câu thần chú sau để biến đổi khu rừng của mình:
Nếu như trong khu rừng không có cây nào ở vị trí ~p~ (~k < p \le n~), nhưng có các cây ở vị trí ~p - 1, p - 2, \ldots, p - k~, vị thần rừng có thể phù phép để gộp ~k~ cây này lại và tạo ra cây một cây mới tại vị trí ~p~. Sau khi phù phép, các cây ở vị trí ~p - 1, p - 2, \ldots, p - k~ sẽ biến mất, và một cây mới tại vị trí ~p~ sẽ mọc lên.
Nếu như trong khu rừng đang có một cây tại vị trí là ~p~ (~k < p \le n~), và không có cây tại các vị trí ~p - 1, p - 2, \ldots, p - k~, vị thần rừng có thể phù phép để biến cây này thành ~k~ cây tại các vị trí nói trên. Sau khi phù phép, cây tại vị trí ~p~ sẽ biến mất, và tại các vị trí ~p - 1, p - 2, \ldots, p - k~ sẽ có các cây mới mọc lên.
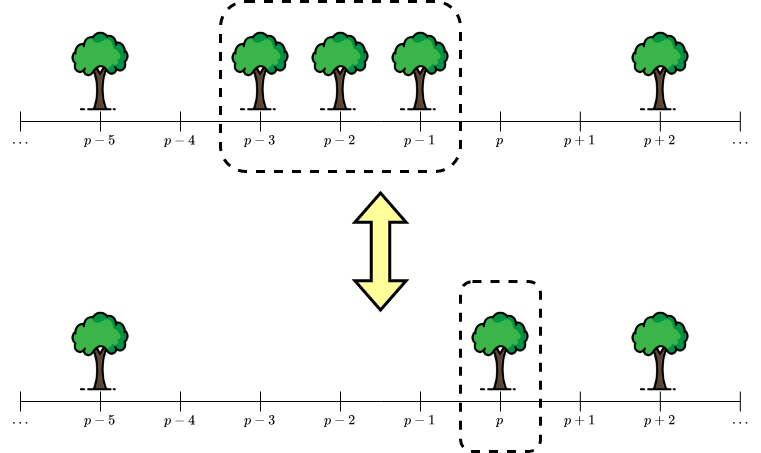
Minh họa cho hai câu thần chú của vị thần rừng với cấp bậc ~k = 3~.
Hiện tại có hai vị thần rừng tập sự có cấp bậc ~k~ là Quang và Tùng.
Quang quản lý khu rừng Q, còn Tùng quản lý khu rừng T. Quang là một
vị thần rừng chăm chỉ, ngày nào cũng luyện tập hai câu thần chú một cách
nhuần nhuyễn để biến đổi khu rừng của mình. Nhưng Tùng thì ngược lại.
Như một chú mèo, Tùng rất thích leo cây trong rừng của mình, nhưng sau
khi leo cây xong thì hay quên đường xuống. Vì thường xuyên bị mắc kẹt
trên cây, nên Tùng cũng không hay luyện tập biến biến đổi khu rừng của
mình.
Sau một thời gian, nhờ chăm chỉ luyện tập, Quang đã làm khu rừng Q của
mình trở nên đẹp đẽ, bạt ngàn. Còn khu rừng T của Tùng do không được
chăm sóc, nên cây cối không được xanh tốt và đẹp đẽ như khu rừng của
Quang. Thầy tình trạng khu rừng của mình như vậy, Tùng cảm thấy thật
ghen tị với Quang. Nhưng cũng biết là lỗi của mình không chịu luyện tập,
nên thay vì bắt nạt Quang, Tùng quyết định sẽ thay đổi một phần của khu
rừng của mình để giống với khu rừng của Quang hơn.
Cho cấp bậc của hai vị thần rừng và các cây trong khu rừng của hai vị thần. Hãy giúp vị thần Tùng trả lời ~q~ câu hỏi sau:
Cho ba số ~l~, ~x~ và ~y~. Xét hai khu rừng con sau:
khu rừng
Xtạo bởi ~l~ vị trí liên tiếp trong khu rừngTbắt đầu từ vị trí ~x~,khu rừng
Ytạo bởi ~l~ vị trí liên tiếp trong khu rừngQbắt đầu từ vị trí ~y~.
Liệu có cách nào để biến đổi khu rừng
Xthành khu rừngYsử dụng hai câu thần chú trên một vài lần (có thể là không lần) không?
Lưu ý rằng Tùng đang xét hai khu rừng X và Y riêng biệt. Hai khu
rừng này đều có ~l~ vị trí đánh số từ ~1~ đến ~l~. Vì hai khu rừng không
có vị trí ~l + 1~, nên Tùng cũng không được phép tạo ra cây tại vị trí
này.
Khu rừng X (sau một vài bước biến đổi) và Y được gọi là giống nhau,
nếu như không tồn tại vị trí nào mà trong một khu rừng có cây, nhưng
tại vị trí tương ứng của khu rừng kia lại trống.
Input
Dòng đầu tiên chứa ba số nguyên ~n~, ~k~ và ~q~ (~k < n \le 10^5~, ~1 \le k \le 5~, ~1 \le q \le 10^5~), lần lượt là dộ dài khu rừng của mỗi vị thần, cấp độ của hai vị thần Quang và Tùng, và số lượng câu hỏi mà Tùng đang phân vân.
Dòng tiếp theo chứa xâu ~T~ có độ dài ~n~ là một xâu nhị phân mô tả
khu rừng T. Vị trí thứ ~i~ trong khu rừng T đang có một cây nếu như
~T_i = 1~, ngược lại vị trí này là vị trí rỗng.
Dòng tiếp theo chứa xâu ~Q~ có độ dài ~n~ là một xâu nhị phân mô tả
khu rừng Q. Vị trí thứ ~i~ trong khu rừng Q đang có một cây nếu như
~Q_i = 1~, ngược lại vị trí này là vị trí rỗng.
Mỗi dòng trong ~q~ dòng tiếp theo chứa ba số nguyên ~l~, ~x~ và ~y~ (~k < l \le n~, ~1 \le x, y \le n - l + 1~) là mô tả cho một câu hỏi của vị thần Tùng.
Output
Với mỗi câu hỏi, in ra YES nếu có thể biến đổi khu rừng X (tạo bởi
~l~ cây liên tiếp trong khu rừng T bắt đầu từ vị trí ~x~) thành khu
rừng Y (tạo bởi ~l~ cây liên tiếp trong khu rừng Q bắt đầu từ vị
trí ~y~). Ngược lại, in ra NO.
Scoring
Subtask 1, tương ứng với ~95~ điểm, có ~n, q \le 3000~
Subtask 2, tương ứng với ~215~ điểm, không có giới hạn gì thêm
Tổng cộng bài toán này có ~310~ điểm.
Sample Input 1
8 2 4
00101001
11011110
3 3 2
3 1 6
5 1 4
4 2 3
Sample Output 1
YES
YES
YES
NO
Notes
Ở câu hỏi đầu tiên, hai phần của khu rừng đã giống nhau (đều có dạng
101).
Ở câu hỏi thứ hai, khu rừng X có dạng 001, và khu rừng Y có dạng
110. Ở khu rừng X, ta có thể biến đổi cây ở vị trí ~3~ thành hai cây
ở vị trí ~1~ và ~2~.
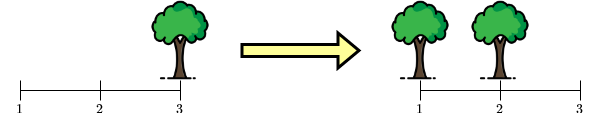
Minh họa phép biến đổi cho câu hỏi thứ hai
Ở câu hỏi thứ ba, khu rừng X có dạng 00101 và khu rừng Y có dạng
11110. Ta có thể thực hiện các biến đổi sau:
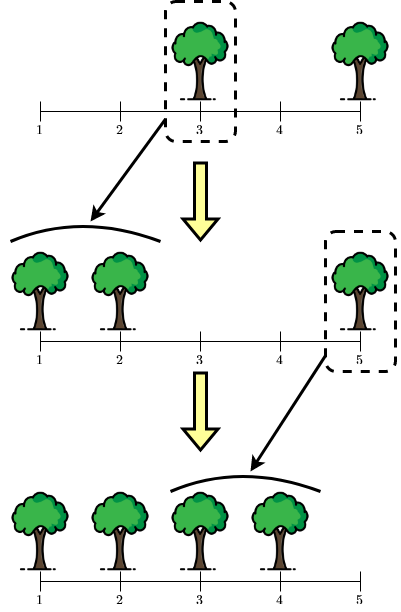
Minh họa phép biến đổi cho câu hỏi thứ ba. Đầu tiên Tùng có thể biến cây tại vị trí ~3~ thành hai câu tại vị trí ~1~ và ~2~. Sau đó biến cây tại vị trí ~5~ thành cây tại vị trí ~3~ và ~4~.
Ở câu hỏi cuối cùng, khu rừng X có dạng 0101, và khu rừng Y có
dạng 0111. Có thể nhận thấy rằng không có cách nào để biến đổi khu
rừng X thành khu rừng Y.
To read the problem statement in English, choose the language using the flag on the navigation bar.
Ngày xửa ngày xưa, có hai chị em cùng cha khác mẹ tên là Cấm và Tám. Mẹ Cấm mất sớm, còn cha Cấm cưới thêm mẹ Tám. Tuy nhiên cha Cấm vô cùng hết mực yêu thương cô. Không may thay, cha Cấm lâm bệnh nặng, không lâu sau đó thì qua đời. Cấm phải sống chung với mẹ ghẻ là mẹ của Tám. Bà mẹ ghẻ là người cay nghiệt, hàng ngày bắt Cấm phải làm việc quần quật, phải làm cho hết mọi công việc trong nhà. Còn Tám thì ngược lại, được mẹ nuông chiều, không những không phải làm gì, mà ngày nào cũng đi chơi la cà, thậm chí còn hay bắt nạt Cấm.
Đến một ngày nọ, nhà Vua có mở hội linh đình, mời tất cả mọi người đến xem hội. Mẹ con Tám đã chuẩn bị tươm tất chuẩn bị đi hội. Nhưng cũng lường trước rằng Cấm cũng sẽ định xin đi cùng, mẹ con Tám đã nghĩ ra mưu kế nhằm không cho Cấm đi. Mẹ ghẻ sai Tám lấy ~n~ cái hũ có nhãn được đánh số từ ~1~ đến ~n~, cái hũ thứ ~i~ đong vào chính xác ~a_i~ hạt gạo. Lúc Cấm xin, mẹ ghẻ thách thức Cấm, bắt Cấm đong đi đong lại các hạt gạo trong ~n~ cái hũ đã cho, sao cho cuối cùng cái hũ thứ ~i~ phải chứa ~b_i~ hạt gạo. Nói xong, mẹ con Tám tức tốc bỏ đi hội, bỏ Cấm ở nhà một mình.
Tưởng chừng lời thách thức đơn giản, xong trong các hũ có rất nhiều gạo, đòi hỏi sự cân đo đong đếm chính xác hơn người để thực hiện. Hiểu được rằng đây là mưu kế bày ra để ngăn mình không đi hội, Cấm bật khóc. Lúc đó ông Bụt hiện lên, hỏi han Cấm. Sau khi nắm được tình hình, ông Bụt bảo Cấm xếp các hũ thành một vòng tròn, sao cho hũ đàu tiên nằm ở bên trái hũ thứ hai, hũ thú hai ở ở bên trái hũ thứ ba, ..., hũ thứ ~n~ ở ở bên trái hũ đầu tiên. Sau đó Bụt gọi hai chú chim xuống giúp Cấm di chuyển gạo. Trong một tích tắc, hai chú chim sẽ cùng nhau thực thao tác sau:
Chú chim đầu tiên sẽ chọn một hạt gạo trong một hũ bất kì, và di chuyển hạt gạo này sang hũ kế tiếp nằm bên trái.
Cùng lúc đó, chú chim thứ hai sẽ chọn một hạt gạo khác trong một hũ bất kì (có thể cùng với hũ mà chú chim đầu tiên đã chọn), và di chuyên hạt gạo này sang hũ kế tiếp nằm bên phải.
Di chuyển duy nhất một hạt gạo là một hành động chậm chạp đối với con người, xong đây là công việc mà hai chú chim có thể làm thoăn thoắt, với độ chính xác tuyệt đối. Chẳng mấy chốc mà hai chú chim có thể giúp Cấm sắp xếp lại các hột thóc thỏa mãn yêu cầu của mẹ ghẻ.
Tuy nhiên, vẫn có trường hợp mà chỉ dựa vào sự giúp đỡ của những chú chim vẫn không thể hoàn thành được thử thách mà mẹ ghẻ đã giao. Cho danh sách lượng gạo ban đầu trong các hũ, và danh sách lượng gạo cần phải đong vào từng cái hũ, hãy giúp Cấm kiểm tra xem có thể đong gạo chỉ với sự trợ giúp của hai chú chim hay không. Trong trường hợp có thể, hãy giúp Cấm tìm số lượng thao tác ít nhất mà hai chú chim cần thực hiện để đong gạo chính xác theo yêu cầu mà mẹ ghẻ đã giao, để Cấm sắp xếp chuẩn bị đi hội.
Input
Mỗi test bao gồm nhiều test case. Dòng đầu tiên chứa số ~t~ (~1 \le t \le 100~) là số lượng test case. Mỗi test case có mô tả như sau.
Dòng đầu tiên của test case chứa số nguyên ~n~ và số ~k~ (~1 \le n \le 10^5~, ~k \in \{0, 1\}~) là số lượng hũ gạo và chỉ số đặc biệt:
khi ~k = 0~, Cấm chỉ muốn kiểm tra xem có cách để hai chú chim tha gạo thỏa mãn yêu cầu của mẹ ghẻ không.
khi ~k = 1~, Cấm muốn tìm số thao tác tối thiểu mà chú chim cần thực hiện để thỏa mãn yêu cầu của mẹ ghẻ.
Hãy xem phần Output để biết thêm thông tin chi tiết.
Dòng tiếp theo chứa ~n~ số nguyên ~a_1, a_2, \ldots, a_n~ (~0 \le a_i \le 10^9~) là số lượng gạo ban đầu trong từng hũ.
Dòng tiếp theo chứa ~n~ số nguyên ~b_1, b_2, \ldots, b_n~ (~0 \le b_i \le 10^9~) là số lượng gạo cần phải đong vào từng hũ.
Dữ liệu đảm bảo tổng số hũ gạo của tất cả các test case trong cùng một test không quá ~10^6~.
Output
Với mỗi test case, nếu như không thể đong gạo chỉ với sự trợ giúp của hai chú chim, hãy in ra ~-1~. Ngược lại:
nếu ~k = 0~, hãy in ra số nguyên không âm bất kì.
nếu ~k = 1~, hãy in ra số thao tác ít nhất mà hai chú chim cần thực hiện để đong gạo thỏa mãn yêu cầu của mẹ ghẻ.
Scoring
Subtask 1, tương ứng với ~60~ điểm, có ~n \le 6~, và tổng số hạt thóc trong tât cả các hũ không quá ~6~.
Subtask 2, tương ứng với ~120~ điểm, có ~k = 0~.
Subtask 2, trương ứng với ~234~ điểm, không có ràng buộc gì thêm.
Tổng cộng bài toán có ~414~ điểm.
Sample Input 1
5
2 1
2 0
0 2
2 0
2 0
1 1
3 1
1 0 1
1 0 1
3 1
4 1 1
1 1 4
3 0
4 1 1
1 1 4
Sample Output 1
1
-1
0
2
1
Notes
Trong test case đầu tiên có duy nhất ~n = 2~ cái hũ, và Cấm muốn tìm số thao tác tối thiểu. Ban đầu chỉ có hũ thứ nhất chứa hai hạt gạo, và cần phải làm cho chỉ duy nhất hũ thứ hai chứa hai hạt gão. Hai chú chim có thể trong một bước di chuyển hai hạt gão này từ hũ thứ nhất sang hũ thứ hai.
Test case thứ hai cũng tương tự như test case thứ nhất, nhưng cần phải làm cho mỗi hũ có duy nhất một hạt gạo. Có thể thấy rằng, ngoài hai trạng thái ~[2, 0]~ và ~[0, 2]~ là hai trạng thái duy nhất có thể của các hũ gạo nếu bắt đầu đong tạo từ trạng thái ~[2, 0]~, nên ở test case này không có cách nào để thỏa mãn yêu cầu của mẹ ghẻ.
Ở test case thứ ba, số lượng gạo trong hũ ban đầu cũng đã khớp với lượng gạo cần đong, nên không cần thực hiện theo tác nào cả.
Tesst case thứ tư và cuối cùng là hai test case tương tự nhau, nhưng test case thứ tư yêu cầu tìm đáp án tối thiểu, trong khi test case thứ năm chỉ yêu cầu kiểm tra xem có cách thỏa mãn yêu cầu của mẹ ghẻ hay không. Cả hai test case đều có ~n = 3~ hũ. Ban đầu các hũ có lượng gạo là ~[1, 1, 4]~, và cần phải đong gạo để cuối cùng các hũ có lượng gạo là ~[4, 1, 1]~. Hai chú chim có thể di chuyển gạo như sau:
| Bước | Hũ gạo chú chim 1 chọn | Hũ gạo chú chim 2 chọn | Lượng gạo trong hũ |
|---|---|---|---|
| (Trước khi bắt đầu) | ~[1, 1, 4]~ | ||
| 1 | Hũ ~3~ | Hũ ~3~ | ~[2, 2, 2]~ |
| 2 | Hũ ~2~ | Hũ ~3~ | ~[4, 1, 1]~ |
Fun fact: Câu truyện mô tả trong đề là câu truyện dựa trên câu chuyện cổ tích Việt Nam Tấm Cám. Song câu chuyện này cũng có nhiều nét tương đồng với câu chuyện Cô bé lọ lem ở châu Âu.