Kỳ thi chọn đội tuyển Olympic 2023 - Ngày 1
Điểm: 100
Hệ thống đường nước thành phố gồm ~N~ trạm được đánh số từ ~0~ đến ~N - 1~ và ~N - 1~ đoạn ống tròn nối giữa các trạm được đánh số từ ~0~ đến ~N - 2~. Giữa hai trạm bất kỳ luôn tồn tại một đoạn ống nối trực tiếp hoặc một dãy đoạn ống liên tiếp dẫn tới nhau thông qua các trạm trung gian. Đoạn ống thứ ~i~ (~0 \le i \le N - 2~) có đường kính là ~D_i~ (mét).
Gọi ~D_{min}~(~x, y~) là đường kính nhỏ nhất trong các đoạn ống nối từ trạm ~x~ đến trạm ~y~ bằng con đường đi qua ít đoạn ống nối nhất, khi đó:
Chi phí thi công để nước có thể đi vào từ trạm vào ~w~ và đi ra ở trạm ra ~u~ được tính bằng: ~D_{min}(w, u) \cdot H~, với ~H~ là hệ số chi phí.
Đối với một trạm vào ~w~ và hai trạm ra ~u~ và ~v~ (~w \neq u~, ~w \neq v~, ~u~ và ~v~ có thể trùng nhau), chi phí thi công là: ~f(w, u, v) = \max(D_{min}(w, u) \cdot H, D_{min}(w, v) \cdot H)~.
Với một chi phí đầu tư ~c~ và hai trạm ra ~u~ và ~v~, Ban quản lý hệ thống đường nước muốn tìm ra tập ~S~ gồm nhiều nhất các trạm vào sao cho ~\sum_{w \in s} f(w, u, v) \le c~ và ~u, v \notin S~.
Yêu cầu: Hãy giúp ban quản lý trả lời ~Q~ câu hỏi như trên.
Chi tiết cài đặt
Thí sinh cần cài đặt hai hàm sau:
void init(const vector<int> &A, const vector<int> &B, const vector<int> &D, int H)
Hàm nhận vào các tham số mô tả hệ thống đường nước;
~H~: hệ số chi phí;
~A~, ~B~, ~D~: các vector chứa ~n - 1~ phần tử, với mỗi số nguyên ~i~ (~0 \le i \le n - 2~), có một đoạn ống nối trực tiếp hai trạm ~A[i]~ và ~B[i]~ với đường kính ~D[i]~.
Hàm này được gọi đúng một lần, trước bất kỳ lệnh gọi nào đến hàm query.
int query(int u, int v, long long c)
Hàm nhận vào ba tham số ~u~, ~v~ và ~c~ mô tả một câu hỏi;
Hàm cần trả về một số nguyên không âm là số lượng phần tử của tập ~S~, nghĩa là số lượng trạm vào nhiều nhất tìm được sao cho ~\sum_{w \in s} f(w, u, v) \le c~ và ~u, v \notin S~.
Hàm này được gọi đúng ~Q~ lần.
Trình chấm mẫu
Tải trình chấm mẫu tại đây.
Trình chấm mẫu đọc dữ liệu vào theo định dạng:
dòng ~1~: ~N~ ~Q~ ~H~
dòng ~2 + i~ (~0 \le i \le N - 2~): ~A[i]~ ~B[i]~ ~D[i]~
dòng ~n + 1 + j~ (~0 \le j \le Q - 1~): ~u~ ~v~ ~c~ với câu hỏi ~j~
Trình chấm mẫu in các kết quả của bạn theo định dạng:
- dòng ~1 + j~ (~0 \le j \le Q - 1~): giá trị trả về của query cho câu hỏi ~j~
Ràng buộc
~1 \le N \le 25 \cdot 10^4~, ~1 \le Q \le 75 \cdot 10^4~, ~1 \le H \le 2023~.
Các tham số truyền vào hàm init thỏa mãn ~0 \le A[i], B[i] \le N - 1~ và ~1 \le D[i] \le 10^9~.
Các tham số truyền vào hàm query thỏa mãn ~0 \le u, v \le N - 1~ và ~1 \le c \le 10^{18}~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~6~ | ~N \le 5000~ và ~Q \le 1000~ |
| 2 | ~19~ | ~D[i] \le 20~ |
| 3 | ~22~ | Trong tất cả các lần gọi hàm query, ~u = v~. |
| 4 | ~20~ | Mỗi trạm được nối trực tiếp tới không quá hai trạm khác. |
| 5 | ~18~ | ~Q \le 200000~ |
| 6 | ~15~ | Không có ràng buộc gì thêm. |
Sample Input 1
6 4 1
0 1 2
0 2 4
0 3 3
3 4 1
3 5 2
4 5 7
0 4 6
1 2 8
3 3 11
Sample Output 1
3
2
3
5
Notes
Dưới đây là một ví dụ về việc gọi hàm:
init([0, 0, 0, 3, 3], [1, 2, 3, 4, 5], [2, 4, 3, 1, 2], 1)
Hàm khởi tạo hệ thống đường nước giống như mô tả ở hình bên dưới.
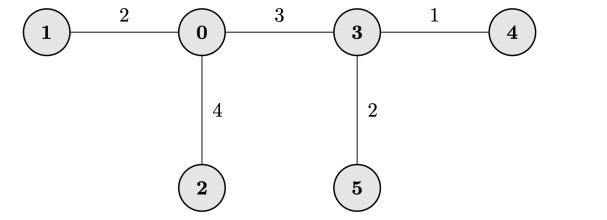
query(4, 5, 7)
Hàm trả về ~3~, một tập ~S~ gồm nhiều trạm nhất thỏa mãn là ~\{0,1,2\}~, khi đó: ~f(0,4,5)=2~; ~f(1,4,5)=2~; ~f(2,4,5) = 2~.
query(0, 4, 6)
Hàm trả về ~2~, một tập ~S~ gồm nhiều trạm nhất thỏa mãn là ~\{1,2\}~, khi đó ~f(1,0,4)=2~; ~f(2,0,4)=4~.
query(1, 2, 8)
Hàm trả về ~3~, một tập ~S~ gồm nhiều trạm nhất thỏa mãn là ~\{0,3,4\}~, khi đó: ~f(0,1,2)=4~; ~f(3,1,2)=3~; ~f(4,1,2)=1~.
query(3, 3, 11)
Hàm trả về ~5~, tập ~S~ gồm nhiều trạm nhất thỏa mãn là ~\{0,1,2,4,5\}~.
Điểm: 100
Xét chuỗi hạt ~S~ có ~n~ hạt, mỗi hạt có thể có màu trắng hoặc màu đen. Ta có thể biểu diễn chuỗi hạt như một xâu nhị phân ~S~ độ dài ~n~, trong đó ~0~ biểu diễn cho màu trắng và ~1~ biểu diễn cho màu đen. Các vị trí trên chuỗi hạt được đánh số bắt đầu từ ~0~.
Xét các định nghĩa sau:
Hai chuỗi hạt ~S~ và ~T~ được gọi là tương đồng nếu tồn tại giá trị ~j~ ~(0 \le j \le n - 1)~ sao cho ~S_i = T_{(i + j) \bmod n}~ với mọi ~0 \le i \le n - 1~.
Hai chuỗi hạt ~S~ và ~T~ được gọi là đối xứng nếu xâu ~S~ và xâu đảo ngược của xâu ~T~ là tương đồng.
Cho hai số nguyên dương ~n~, ~k~ và xâu nhị phân ~P~ độ dài ~k~. Cần tìm một tập ~U~ gồm các chuỗi hạt độ dài ~n~ thỏa:
Mọi xâu biểu diễn của các chuỗi hạt đều có tiền tố độ dài ~k~ là xâu ~P~.
Mọi cặp chuỗi hạt trong tập không tương đồng hay đối xứng nhau.
Tập ~U~ có nhiều chuỗi hạt nhất có thể.
Bạn cần cho biết độ dài lớn nhất của tập ~U~ có thể tạo ra.
Input
Dòng đầu tiên gồm hai số nguyên dương ~n~, ~k~ ~(1 \le n \le 10^9, 1 \le k \le min(n, 20))~.
Dòng thứ hai gồm một xâu ~P~ độ dài ~k~ chỉ gồm các kí tự ~0~ và ~1~.
Output
In ra kích thước lớn nhất của tập ~U~ có thể có. Vì đáp án có thể rất lớn, in ra đáp án modulo ~10^9+7~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~11~ | ~n\le 22~ |
| 2 | ~13~ | ~k = 1, n \le 10^5~ |
| 3 | ~12~ | ~k = 2, n \le 10^5~, ~n~ là số nguyên tố |
| 4 | ~20~ | ~n \le 10^5~ |
| 5 | ~20~ | ~n~ là số nguyên tố |
| 6 | ~24~ | Không có ràng buộc gì thêm |
Sample Input 1
6 3
001
Sample Output 1
7
Điểm: 100
Có ~n~ bạn đang chơi trên một đồ thị liên thông, vô hướng, có trọng số gồm ~n~ đỉnh và ~m~ cạnh. Trọng số của các cạnh phân biệt đôi một.
Trên mỗi đỉnh của đồ thị có một người chơi đang cầm súng nước. Mỗi người chơi sẽ bắn súng nước vào người chơi ở gần người chơi đó nhất (với mỗi người chơi thì luôn có ít nhất một cạnh nối tới người đó). Người không bị ai bắn nước vào (nếu có) sẽ dành chiến thắng.
Bạn là ~1~ trong ~n~ người chơi, tuy nhiên bạn chỉ biết ~n~.
Bạn được hỏi các câu hỏi có dạng sau: ~S\ W~
~S~ là một tập con không rỗng của tập ~\{1, 2, ..., n\}~
~W~ là một số nguyên dương không vượt quá ~3 \cdot 10^6~.
Máy sẽ trả về ~1~ nếu tồn tại 2 đỉnh ~u, v \in S~ thỏa mãn có một cạnh nối giữa chúng với trọng số ~\leq w~ và ~0~ nếu không tồn tại 2 đỉnh như vậy.
Các bạn cần tìm đỉnh đảm bảo mình chiến thắng (nếu có) hoặc ~-1~ nếu không tồn tại một đỉnh nào như vậy
Implementation
Thí sinh cần cài đặt hàm sau:
int play(int n)
Tham số ~n~ là số người chơi (cũng như số đỉnh của đồ thị)
Hàm cần trả về một số nguyên là chỉ số đỉnh đảm bảo giành chiến thắng (hoặc ~-1~ nếu không tồn tại)
Thí sinh được phép gọi hàm sau:
int ask(vector<int> S, int W)
Hàm sẽ trả về ~1~ nếu tồn tại 2 đỉnh ~u, v \in S~ thỏa mãn có một cạnh nối giữa chúng với trọng số ~\leq w~ và ~0~ nếu không tồn tại 2 đỉnh như vậy.
Lưu ý: Thí sinh cần phải khai báo thư viện bằng dòng lệnh #include "gungame.h" ở đầu chương trình. Thí sinh được phép khai báo thêm hàm và biến bên ngoài, nhưng không được khai báo hàm tên là main.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | ~10~ | ~n = 65~ |
| ~2~ | ~20~ | ~n = 1000~, đồ thị là cây, mỗi đỉnh có bậc không quá ~2~ |
| ~3~ | ~30~ | ~n \leq 1000~, đồ thị là cây |
| ~4~ | ~40~ | ~n = 2023~ |
Gọi ~d~ là số lần bạn hỏi trong một test, ~D = max(d)~ với mọi test trong một subtask và ~T~ là điểm của subtask đó, điểm của bạn sẽ được tính như sau:
| D | Điểm |
|---|---|
| ~D \leq 41000~ | ~T~ |
| ~41000 \le D \leq 45000~ | ~0.8 \times T~ |
| ~45000 \le D \leq 50000~ | ~0.5 \times T~ |
| ~50000 \le D \leq 60000~ | ~0.3 \times T~ |
| ~60000 \le D~ | ~0~ |
Sample grader
Tải trình chấm mẫu tại đây.
- Trình chấm mẫu đọc dữ liệu theo định dạng:
- ~N\ M~
- dòng ~1+i~ (~1\le i\le M~): ~U[i]\ V[i]\ W[i]~ thể hiện các cạnh của đồ thị
- Trình chấm mẫu in ra theo định dạng:
- Kết quả hàm
play - Số truy vấn
askđã dùng
- Kết quả hàm