Educational SQRT Contest (Part 2)
Điểm: 100
Cho một đồ thị vô hướng gồm ~n~ đỉnh và ~m~ cạnh. Có ~2~ loại thao tác cần thực hiện:
~1.~ Thêm ~1~ cạnh giữa ~2~ đỉnh ~a~ và ~b~.
~2.~ Xóa ~1~ cạnh giữa ~2~ đỉnh ~a~ và ~b~. Dữ liệu đảm bảo tồn tại cạnh giữa đỉnh ~a~ và ~b~ trước khi xóa.
Nhiệm vụ của bạn là đếm số thành phần liên thông của đồ thị sau mỗi thao tác được thực hiện
Input
Dòng đầu tiên gồm ~3~ số nguyên ~n, m, k~ (~2 \le n \le 10^5, 1 \le m, k \le 10^5~)
~m~ dòng tiếp theo, mỗi dòng gồm ~2~ số ~a, b~ là ~1~ cạnh của đồ thị ban đầu. Có tối đa ~1~ cạnh giữa ~2~ đỉnh bất kì. (~1 \le a, b \le n~)
~k~ dòng tiếp theo, mỗi dòng gồm ~3~ số ~t, a, b~. Khi ~t = 1~ (thêm cạnh) hoặc ~t = 2~ (xóa cạnh). ~1~ cạnh được thêm giữa ~2~ đỉnh khi chưa tồn tại cạnh giữa ~2~ đỉnh đó, và chỉ cạnh đã tồn tại có thể được xóa.
Output
In ra ~k + 1~ số: đầu tiên là số thành phần liên thông trước khi các thao tác diễn ra, và số thành phần liên thông sau mỗi thao tác biến đổi.
Sample Input 1
5 3 3
1 4
2 3
3 5
1 2 5
2 3 5
1 1 2
Sample Output 1
2 2 2 1
Điểm: 100
Cho một tập ~S~ chứa các cặp số nguyên ~(a,b)~. Ban đầu ~S~ rỗng.
Bạn được cho ~n~ truy vấn, truy vấn thứ ~i~ thuộc một trong ba dạng sau:
~1.~ Thêm cặp số nguyên ~(a,b)~ vào tập ~S~.
~2.~ Xóa cặp số nguyên ~(a,b)~ đã thêm vào ở truy vấn thứ ~x~. Biết các truy vấn được đánh số từ ~1~ tới ~n~.
~3.~ Với số ~q~ cho trước, hãy tìm giá trị lớn nhất của biểu thức ~a\times q + b~ với mọi cặp ~(a,b)~ trong tập ~S~.
Hãy xử lí toàn bộ các truy vấn này.
Input
Dòng đầu tiên chứa số nguyên dương ~n~ ~(1 \le n \le 3 \times 10^5)~ miêu tả số truy vấn.
Trong ~n~ dòng sau, mỗi dòng đều bắt đầu bằng giá trị ~t~ ~(1 \le t \le 3)~ miêu tả loại của truy vấn.
Với trường hợp ~t=1~, bạn sẽ nhận được hai giá trị ~a,b~ ~(|a|, |b| \le 10^9)~ miêu tả cặp số nguyên ~(a,b)~.
Với trường hợp ~t=2~, bạn sẽ nhận được giá trị ~x~ miêu tả thứ tự truy vấn của cặp cần xóa. Dữ liệu đảm bảo rằng ~x~ bé hơn thứ tự của truy vấn hiện tại, truy vấn ~x~ là truy vấn loại ~1~ và truy vấn này chưa bị xóa trước đó.
Với trường hợp ~t=3~, bạn sẽ nhận được giá trị ~q~ ~(|q| \le 10^9)~.
Output
In ra giá trị lớn nhất của biểu thức ~a \times q + b~ cho mọi truy vấn loại ~3~.
Nếu tập ~S~ đang rỗng, hãy in ra "EMPTY SET".
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~30~ | ~n \le 2000~ |
| 2 | ~30~ | Không tồn tại truy vấn loại ~2~ |
| 3 | ~40~ | Không có ràng buộc gì thêm |
Sample Input 1
7
3 1
1 2 3
3 1
1 -1 100
3 1
2 4
3 1
Sample Output 1
EMPTY SET
5
99
5
Bạn được cho một dãy số, ban đầu dãy rỗng và bạn phải thực hiện ~Q~ truy vấn thuộc ~1~ trong ~3~ loại:
~add\ s~: Thêm một số có giá trị ~s~ vào dãy, lưu ý một dãy có thể có một vài số xuất hiện nhiều lần.
~del\ s~: Xóa đi một bản sao của số ~s~ trong dãy, đề luôn đảm bảo dãy có ít nhất một số mang giá trị ~s~ khi đưa ra truy vấn này
~cnt\ s~: Đếm số số ~a~ ở trong dãy thỏa điều kiện ~a\ AND\ s\ =\ a~
Input
Dòng đầu chứa số nguyên dương ~Q(1 \leq Q \leq 2\times 10^5)~
~Q~ dòng sau đó chữa một xâu truy vấn ~T~ và một số nguyên ~s (0 \leq s \le 2^{16})~
Output
Với mỗi truy vấn dạng ~cnt\ s~, in ra đáp án trên một dòng
Sample Input 1
7
add 11
cnt 15
add 4
add 0
cnt 6
del 4
cnt 15
Sample Output 1
1
2
2
Notes
Trong truy vấn ~cnt\ s~ đầu tiên, dãy số chúng ta có ~15\ AND\ 11=11~ nên đáp án cho truy vấn là ~1~
Trong truy vấn ~cnt\ s~ thứ hai, dãy số chúng ta có ~6\ AND\ 0=0~ và ~6\ AND\ 4=4~ nên đáp án cho truy vấn là ~2~
Trong truy vấn ~cnt\ s~ thứ ba, dãy số chúng ta có ~15\ AND\ 11=11~ và ~15\ AND\ 0=0~ nên đáp án cho truy vấn là ~2~
Điểm: 100
Trụ sở của VNOI mới đây đã được xây dựng lại vô cùng hiện đại và hoành tráng. Do được quản lý bởi các nhà lập trình viên tài năng trên khắp đất nước Việt Nam, cấu trúc của trụ sở mới này cũng được thiết kế vô cùng đặc biệt. Tòa nhà có ~n~ căn phòng được đánh số lần lượt từ ~1~ đến ~n~. Các căn phòng được kết nối với nhau bởi ~n - 1~ hành lang đảm bảo rằng từ một căn phòng có thể đi đến bất cứ căn phòng nào khác trong tòa nhà. Ở tòa nhà này, ban đầu sẽ chỉ có căn phòng ~1~ được bật đèn và trong ~n - 1~ căn phòng còn lại đèn sẽ tắt. Thời gian tới, tòa nhà sẽ chào đón thêm các nhân viên chuyển đến nên sẽ phải bật thêm đèn ở một số căn phòng, những lần như vậy ban quản lý tòa nhà sẽ thông báo bật điện tại một căn phòng nào đó. Là một nhân viên mới ở VNOI, mỗi lần làm việc, bạn phải tiếp đón một khách hàng tại căn phòng được chỉ định sẵn và bạn sẽ phải tìm độ dài đường đi ngắn nhất từ từ căn phòng được chỉ định ấy đến một căn phòng được bật sáng gần nhất để có thể chuẩn bị cho buổi làm việc của mình.
Input
Dòng đầu tiên chứa số ~n~ và ~m~ cho biết số phòng của tòa nhà và tổng số lần bật đèn ở các căn phòng cũng như số lần mà bạn phải làm việc với khách hàng. ~(1 \leq n,m \leq 10^5)~
~n - 1~ dòng tiếp theo mỗi dòng chứa 2 số ~u~ ~v~ thể hiện có một hành lang kết nối giữa phòng ~u~ và phòng ~v~ ~(1 \leq u,v \leq n)~
~m~ dòng cuối mỗi dòng chứa ~1~ cặp số ~(t,u)~ cho biết ~2~ loại truy vấn:
- ~1~ ~u~ : Bật đèn ở phòng ~u~.
- ~2~ ~u~ : Cho biết độ dài đường đi ngắn nhất từ một căn phòng đang được bật sáng tới phòng ~u~.
Dữ liệu đảm bảo các truy vấn đều đúng với mô tả đề bài.
Output
Gồm một số dòng mỗi dòng là câu trả lời cho truy vấn loại ~2~
Scoring
Scoring table:
| Group | Add. constraints | Points |
|---|---|---|
| ~1~ | ~n, m \le 10^3~ | ~10~ |
| ~2~ | ~n \le 10^3, m \le 10^5~ | ~20~ |
| ~3~ | ~n, m \le 10^5~ | ~70~ |
Sample Input 1
5 4
1 2
2 3
2 4
4 5
2 1
2 5
1 2
2 5
Sample Output 1
0
3
2
Điểm: 100
DeMen100ns đang có một mạng lưới giao thông với ~n~ thành phố và ~m~ con đường hai chiều. Anh ấy được giao việc phải chọn ra ~3~ thành phố phân biệt ~(i, j, k)~ sao cho:
- Tồn tại các con đường nối ~(i - j)~, ~(j - k)~ và ~(k - i)~.
Vì không biết phải chọn ra các thành phố nào, DeMen100ns muốn biết số cách anh ấy có thể chọn ra cặp ~3~ thành phố thỏa mãn điều kiện trên. Hãy giúp DeMen100ns đếm xem có bao nhiêu cách anh ấy có thể chọn.
Dữ liệu đảm bảo chỉ tồn tại nhiều nhất một con đường nối giữa hai thành phố.
Input
Dòng đầu tiên chứa hai số nguyên dương ~n~ và ~m~ ~(2 \le n \le 10^5, 1 \le m \le 2 * 10^5)~.
~m~ dòng tiếp theo dòng thứ ~i~ chứa hai số nguyên dương ~u~, ~v~ ~(1 \le u, v \le n, u \ne v)~ — có một con đường nối giữa thành phố ~u~ và thành phố ~v~.
Output
In ra một số duy nhất là kết quả của bài toán.
Sample Input 1
4 6
1 2
1 3
1 4
2 3
2 4
3 4
Sample Output 1
4
Điểm: 100
Bạn được cho một dãy số ~A_1~, ~A_2~, ..., ~A_n~ và ~m~ tập hợp ~S_1~, ~S_2~, ..., ~S_m~ các chỉ số của mảng này. Gọi ~S_k = \{S_{k, i}\}, 1 \leq i \leq |S_k|~. Nói cách khác, ~S_{k, i}~ là một phần tử bất kỳ từ tập hợp ~S_k~.
Trong bài này bạn sẽ phải trả lời ~q~ truy vấn có 2 dạng sau:
~?\ k~: Tính tổng ~\displaystyle \sum^{|S_k|}_{i = 1}{A_{S_{k, i}}}~, hay tổng các phần tử có vị trí thuộc tập ~S_k~ của dãy ~A~.
~+\ k\ x~: Cộng ~x~ vào các phần tử của dãy ~A~ có chỉ số trong tập ~S_k~. Phần tử ~A_{S_{k, i}}~ được thay bằng ~A_{S_{k, i}} + x~ với mọi ~i \in [1, |S_k|]~.
Với mỗi truy vấn loại đầu tiên hãy in tổng đã tính.
Input
Dòng đầu tiên gồm 3 số ~n, m, q~ (~1 \leq n, m, q \leq 10^5~). Dòng thứ hai gồm ~n~ phần tử ~A_1, A_2, \cdots, A_n~ (~|A_i| \leq 10^8~), các phần tử của dãy ~A~.
~m~ dòng tiếp theo, dòng thứ ~k~ gồm một số nguyên dương ở đầu cho biết số lượng phần tử của tập ~S_k~, theo sau bởi ~|S_k|~ số nguyên dương phân biệt ~S_{k, 1}, S_{k, 2}, \cdots, S_{k, |S_k|}~ (~1 \leq S_{k, i} \leq n~).
~q~ dòng tiếp theo, mỗi dòng có dạng ~?\ k~ hoặc ~+\ k\ x~. Với mọi truy vấn có ~1 \leq k \leq m~, ~|x| \leq 10^8~. Các truy vấn được cho theo thứ tự chúng cần được trả lời.
Đề đảm bảo tổng của kích thước mọi tập ~S_k~ không quá ~10^5~.
Output
Sau mỗi truy vấn dạng đầu tiên hãy in tổng đã tính trên một dòng.
Sample Input 1
5 3 5
5 -5 5 1 -4
2 1 2
4 2 1 4 5
2 2 5
? 2
+ 3 4
? 1
+ 2 1
? 2
Sample Output 1
-3
4
9
Notes
Ở truy vấn đầu tiên, tập ~S_k~ là ~S_2~ có 4 phần tử ~\{2, 1, 4, 5\}~. Tổng của 4 phần tử có vị trí trong tập ~S_2~ là ~A_2 + A_1 + A_4 + A_5 = -5 + 5 + 1 + (-4) = -3~.
Điểm: 100
Đất nước Bình Dương có ~n~ thành phố và ~m~ đường đi hai chiều giữa chúng. Các thành phố được đánh số từ ~1~ đến ~n~. Con đường thứ ~i~ có màu ~c_i~, kết nối thành phố ~a_i~ với thành phố ~b_i~.
Để giải quyết vấn nạn tắc đường, tổng thống Bình Dương đưa ra ~q~ câu hỏi.
Câu hỏi thứ ~i~ gồm hai số nguyên ~u_i~ và ~v_i~.
Tìm số lượng màu thỏa mãn: Với mỗi màu, chỉ dùng những con đường có màu này có thể đi từ thành phố ~u_i~ tới ~v_i~.
Input
Dòng đầu chứa hai số nguyên ~n~ và ~m~ (~2 \le n \le 10^5~, ~1 \le m \le 10^5~) — số thành phố và số con đường.
~m~ dòng tiếp theo, mỗi dòng chứa ba số nguyên ~a_i~, ~b_i~ và ~c_i~ (~1 \le a_i < b_i \le n~ và ~1 \le c_i \le m~).
Lưu ý các con đường là hai chiều, có thể có nhiều con đường giữa hai thành phố. Tuy nhiên, không có nhiều con đường cùng màu giữa hai thành phố, nói cách khác, nếu ~i \ne j~ thì ~(a_i, b_i, c_i) \ne (a_j, b_j, c_j)~.
Dòng tiếp theo chứa số nguyên ~q~ (~1 \le q \le 10^5~) — số lượng câu hỏi.
~q~ dòng cuối cùng, mỗi dòng chứa hai số nguyên ~u_i~ và ~v_i~ (~1 \le u_i, v_i \le n~ và ~u_i \ne v_i~).
Output
Với mỗi câu hỏi, in ra đáp án trên một dòng.
Sample Input 1
4 5
1 2 1
1 2 2
2 3 1
2 3 3
2 4 3
3
1 2
3 4
1 4
Sample Output 1
2
1
0
Sample Input 2
5 7
1 5 1
2 5 1
3 5 1
4 5 1
1 2 2
2 3 2
3 4 2
5
1 5
5 1
2 5
1 5
1 4
Sample Output 2
1
1
1
1
2
Notes
Ở ví dụ thứ nhất:
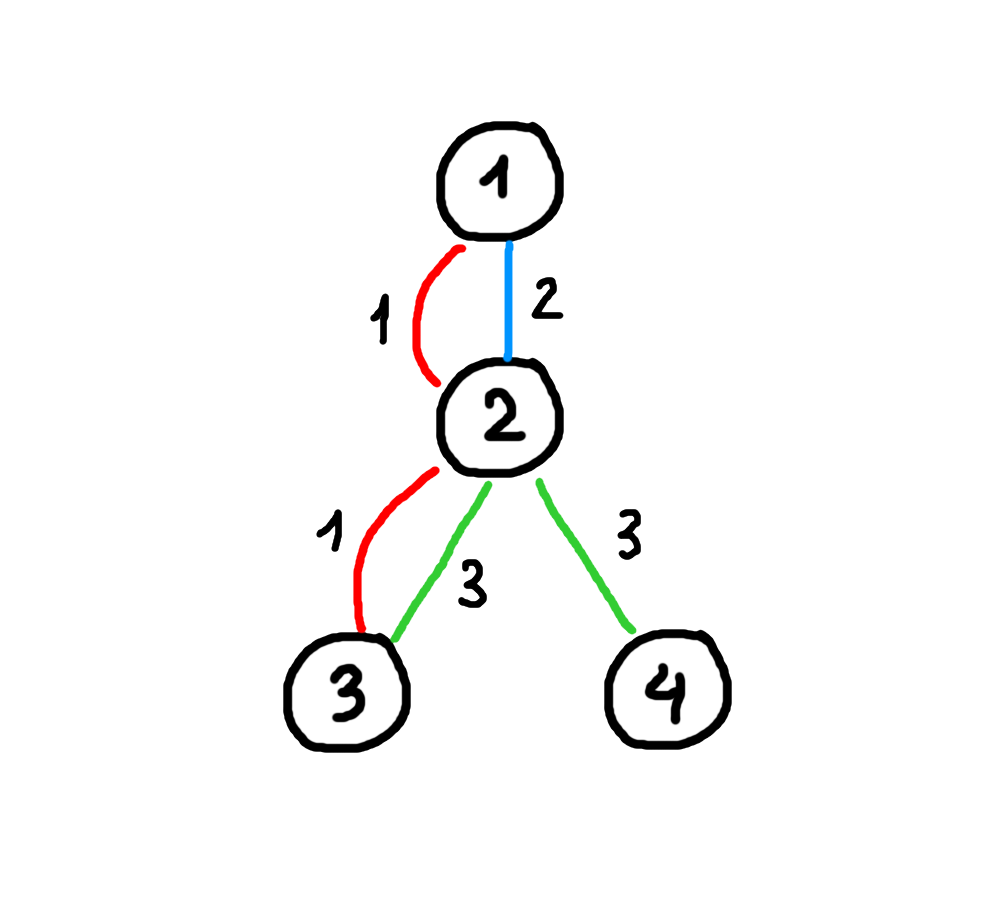
Có thể kết nối thành phố ~1~ với thành phố ~2~ chỉ dùng màu ~1~ hoặc chỉ dùng màu ~2~.
Có thể kết nối thành phố ~3~ với thành phố ~4~ chỉ dùng màu ~3~.
Không thể kết nối thành phố ~1~ với thành phố ~4~ nếu chỉ dùng một màu.
Điểm: 100
Demen có ~N~ đoạn, đoạn thứ ~i \space (1 \leq i \leq n)~ bắt đầu ở ~L_{i}~ và kết thúc ở ~R_{i}~. Đoạn thẳng này đi qua mọi điểm ~x~ thỏa mãn ~L_{i} \leq x \leq R_{i}~.
Demen có ~Q~ câu hỏi, mỗi câu hỏi có dạng ~X_{1}, X_{2}, ..., X_{M}~. Bạn cần tính số đoạn trong ~N~ đoạn trên thỏa mãn: số điểm mà đoạn thẳng đó đi qua trong ~M~ điểm trên là lẻ.
Input
Dòng đầu tiên chứa số ~T \space (T \leq 100)~ là số test case cho bài này
Mỗi test có dạng như sau
Dòng đầu tiên của mỗi test chứa số ~N \space (N \leq 10^5)~ là số đoạn
~N~ dòng từ dòng ~2~ đến ~N + 1~, dòng thứ ~(i + 1)~ gồm 2 số ~L_{i}~ và ~R_{i}~ ~(1 \leq L_{i} \leq R_{i} \leq N)~ biểu diễn đoạn thứ ~i~
Dòng thứ ~N + 2~ chứa số ~Q \space (Q \leq 10^5)~ là số truy vấn
~Q~ dòng cuối cùng biểu diễn các truy vấn, bắt đầu bằng số ~M~, và sau đó là ~M~ điểm ~X_{1}, X_{2}, ..., X_{M} \space (1 \leq X_{i} \leq N)~ đôi một phân biệt. Dữ liệu đảm bảo tổng số điểm trong tất cả các truy vấn trong bộ test ~\leq N~
Dữ liệu đảm bảo tất cả các số trong input nguyên dương, và tổng ~N, Q~ trong tất cả các truy vấn ~\leq 2 * 10^5~
Output
Với mỗi truy vấn, in ra đáp án của truy vấn đó (theo đúng thứ tự), mỗi số trên một dòng.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~10~ | ~N, Q \leq 300~ |
| 2 | ~90~ | Không có điều kiện gì thêm |
Sample Input 1
2
5
4 5
3 5
2 4
1 3
5 5
2
4 1 2 3 4
1 4
5
4 5
3 5
2 4
2 3
5 5
2
2 2 5
3 1 2 5
Sample Output 1
3
3
5
5
Điểm: 100
Bài đang bị tạm khoá, time limit được set rất thấp
Một xâu nhị phân ~t~ được gọi là tuyệt vời nếu đồng thời thỏa mãn 2 điều kiện sau đây:
Tồn tại ít nhất một ký tự 1 trong xâu
Độ dài của xâu ~t~ chia hết cho số lượng ký tự 1 trong xâu. Ví dụ: 1, 1010, 111 đều là các xâu tuyệt vời; còn 0, 110, 01010 thì không.
Cho xâu nhị phân ~s~, đếm số lượng xâu con của ~s~ là xâu tuyệt vời.
Xâu ~a~ được gọi là xâu con của xâu ~b~ khi xóa đi một vài ký tự (có thể là ~0~) ở đầu và một vài ký tự (có thể là ~0~) ở cuối xâu ~b~ thì có được xâu ~a~.
Input
Gồm một dòng duy nhất chứa xâu nhị phân ~s~ (~1\leq |s|\leq 100\ 000~) chỉ bao gồm các ký tự 0 và 1.
Output
Gồm một dòng duy nhất chứa số nguyên dương là số xâu con tuyệt vời của ~s~.
Sample Input 1
111
Sample Output 1
6
Sample Input 2
01010
Sample Output 2
10
Sample Input 3
0000
Sample Output 3
0
Sample Input 4
1111100000
Sample Output 4
25
Notes
Trong ví dụ đầu tiên, tất cả xâu con của ~s~ đều tuyệt vời.
Trong ví dụ thứ hai, các xâu con tuyệt vời của ~s~ là: 1 (~2~ lần), 01 (~2~ lần), 10 (~2~ lần), 010 (~2~ lần), 1010, 0101.
Trong ví dụ thứ ba, không có xâu con nào tuyệt vời.