Educational RMQ Contest
[placeholder] đã ngồi nghĩ 3 ngày 3 đêm nhưng không ra được cốt truyện cho bài này.
Cho bảng ~M~ kích thước ~n \times n~ gồm các số nguyên dương. Bạn phải xử lý ~q~ truy vấn gồm 2 loại:
- ~1\; x\; y\; z~: Tìm số lớn nhất trong bảng con ~z \times z~ có góc trên-trái là ô ~(x,y)~. Ô trên-trái của bảng là ô ~(1,1)~.
- ~2\; x\; y~: Dịch (cyclic shift) bảng ~x~ ô theo chiều dọc và ~y~ ô theo chiều ngang. Hình dưới minh họa bảng ~4 \times 4~ với ~x=2~ và ~y=1~.
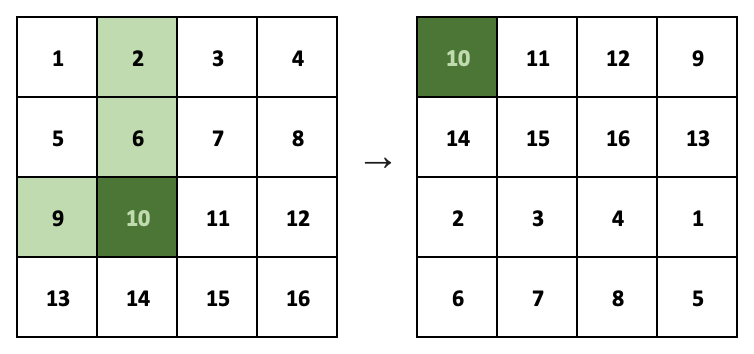
Lưu ý: Do kích thước lớn, để giảm thời gian nhập-xuất, input-output của bài toán được xử lý đặc biệt.
Input
Dòng đầu tiên chứa 2 số ~n, q~ (~n \leq 1,000~, ~q \leq 2,000,000~).
Dòng tiếp theo chứa 2 số ~A_0, B_0~ (~A, B < 10^9+7~).
Dòng cuối cùng chứa 4 số ~C_0, D_0, E_0, F_0~ (~C < 10^9+7, D, E, F < n~).
Với ~i \geq 1~:
Các dãy ~A, B, C~ được định nghĩa như sau:
- ~X_1~ = ~1+((X_0*X_0)\; mod\; 10^9+7)~
- ~X_i~ = ~1+((X_{i-1}+X_{i-2})\; mod\; 10^9+7)\; (i \geq 2)~
Các dãy ~D, E, F~ được định nghĩa như sau:
- ~X_1~ = ~1+((X_0*X_0)\; mod\; n)~
- ~X_i~ = ~1+((X_{i-1}+X_{i-2})\; mod\; n)\; (i \geq 2)~
Dãy ~L~ được định nghĩa như sau: ~L_i = n-max(D_i,E_i)~
Bảng ~M~ được tính bằng công thức:
- ~a_{i,j}: (A_i + B_j)\; mod \; 10^9+7~
Với truy vấn thứ ~i~, nếu ~C_i\; \&\; 1=0~ thì truy vấn đó sẽ có dạng:
- ~1\; D_i\; E_i\; [1+(L_i\; \&\; (L_i \oplus F_i))]~
Ngược lại, nếu ~C_i\; \&\; 1=1~ thì truy vấn đó sẽ có dạng:
- ~2\; D_i\; E_i~
Trong đó: ~\&, \oplus~ là toán tử AND, XOR
Output
Với mỗi ~1,000~ truy vấn loại 1, ta in ra tổng đáp án của các truy vấn đó ~mod\; 10^9+7~ trên các dòng khác nhau.
Ví dụ: Với test có ~3456~ truy vấn loại 1, output có dạng như sau:
~(ans_1\; +\; ...\; +\; ans_{1000})\; mod\; 10^9+7~
~(ans_{1001}\;+\;...\;+\;ans_{2000})\; mod\; 10^9+7~
~(ans_{2001}\;+\;...\;+\;ans_{3000})\; mod\; 10^9+7~
~(ans_{3001}\;+\;...\;+\;ans_{3456})\; mod\; 10^9+7~
Sample Input 1
7 10
2 3
177013 4 5 6
Sample Output 1
262
Notes
Giải thích ví dụ 1:
Bảng số :
| 15 | 19 | 30 | 45 | 71 | 112 | 179 |
| 18 | 22 | 33 | 48 | 74 | 115 | 182 |
| 24 | 28 | 39 | 54 | 80 | 121 | 188 |
| 33 | 37 | 48 | 63 | 89 | 130 | 197 |
| 48 | 52 | 63 | 78 | 104 | 145 | 212 |
| 72 | 76 | 87 | 102 | 128 | 169 | 236 |
| 111 | 115 | 126 | 141 | 167 | 208 | 275 |
Các truy vấn:
| 2 3 5 |
| 2 1 4 |
| 2 5 3 |
| 1 7 1 1 |
| 1 6 5 1 |
| 2 7 7 |
| 2 7 6 |
| 1 1 7 1 |
| 1 2 7 1 |
| 2 4 1 |
Cho dãy ~a_1, a_2, \dots, a_n~ gồm ~n~ số nguyên. Bạn cần trả lời ~q~ truy vấn, mỗi truy vấn gồm hai số nguyên ~l~, ~r~. Với mỗi truy vấn bạn cần đếm xem, có bao nhiêu cách chia dãy ~a_l, a_{l+1}, \dots, a_r~ thành hai phần khác rỗng sao cho mỗi phần gồm các phần tử đứng liên tiếp và đôi một phân biệt.
Input
Dòng đầu chứa hai số nguyên ~n~, ~q~ (~1 \le n, q \le 5 \times 10^5~).
Dòng thứ hai chứa ~n~ số nguyên ~a_1, a_2, \dots, a_n~ (~1 \le a_i \le 10^9~).
~q~ dòng tiếp theo, dòng thứ ~i~ chứa hai số nguyên ~l_i~, ~r_i~ (~1 \le l_i \le r_i \le n~) mô tả truy vấn thứ ~i~.
Output
In ra ~q~ dòng, dòng thứ ~i~ gồm một số nguyên là kết quả cho truy vấn thứ ~i~.
Sample Input 1
8 4
1 3 2 2 4 5 4 6
1 8
1 4
2 7
4 6
Sample Output 1
0
1
0
2
Điểm: 100
Là một cậu học sinh vùi mình trong môn Toán mà lỡ lãng quên mất vẻ đẹp của Văn học, Phúc đang chìm trong sự đau khổ của deadline bài tập làm văn cần phải nộp vào ngày hôm sau. May mắn thay, trước khi cô giáo giao bài tập cô đã gợi ý một số câu trích dẫn hay, và Phúc quyết định sẽ viết tất cả các câu trích dẫn ấy để bài văn của mình có thể gây ấn tượng mạnh với cô.
Cụ thể hơn, cô giáo đã giới thiệu với lớp mình về ~n~ câu trích dẫn hay, và Phúc sẽ viết ra các câu trích dẫn ấy theo đúng thứ tự cô đưa ra trong bài văn của mình. Bằng khả năng cảm thụ văn chương của mình, Phúc đã cảm nhận và đánh giá mỗi câu trích dẫn đều có giá trị nhân sinh nhất định, trong đó câu trích dẫn thứ ~i~ có giá trị nhân sinh là ~a_i~.
Bài văn của Phúc cần phải được bài trí thành nhiều đoạn văn, trong đó mỗi đoạn văn gồm các câu văn liên tiếp. Phúc nhận thấy việc bố trí các câu trích dẫn vào đoạn văn nào là vô cùng quan trọng, bởi theo Phúc mọi đoạn văn đều được đặc trưng bởi giá trị ngưng kết là giá trị nhân sinh lớn nhất trong số các câu trích dẫn của đoạn văn đó. Để bài văn của Phúc được hay, mỗi đoạn văn của Phúc đều phải có ít nhất ~1~ câu trích dẫn, khi đó giá trị lắng đọng của bài văn của Phúc sẽ là ước chung lớn nhất của tất cả các giá trị ngưng kết của các đoạn văn.
Một bài văn của Phúc chỉ hoàn chỉnh khi nó có đúng ~k~ đoạn văn, và bài văn của Phúc có giá trị ngưng kết càng lớn thì bài văn của Phúc sẽ càng hay và dễ đạt điểm cao từ cô hơn.
Các bạn hãy giúp Phúc hoàn thành deadline và thể hiện khả năng văn chương lai láng nhé!
Input
Dòng đầu tiên gồm 2 số nguyên dương ~n, k~ ~(1 \le k \le n \le 10^5)~ - số lượng câu trích dẫn mà cô giáo đã giới thiệu cho lớp và số đoạn văn Phúc dự tính sẽ chia ra trong bài văn của mình.
Dòng tiếp theo gồm ~n~ số nguyên dương ~a_1, a_2,..., a_n~ ~(1 \le a_i \le 10^6~, ~\forall i \in [1, n])~ - giá trị nhân sinh của từng câu trích dẫn.
Output
Gồm ~1~ số nguyên dương duy nhất là giá trị lắng đọng lớn nhất mà bài văn của Phúc có thể đạt được.
Scoring
Subtask ~1~ ~(10\%)~: ~1 \le k \le n \le 10^2~, ~1 \le a_i \le 10^6~
Subtask ~2~ ~(15\%)~: ~1 \le k \le n \le 3 \cdot 10^3~, ~1 \le a_i \le 10^6~
Subtask ~3~ ~(25\%)~: ~1 \le k \le n \le 10^5~, ~1 \le a_i \le 2 \cdot 10^2~
Subtask ~4~ ~(50\%)~: ~1 \le k \le n \le 10^5~, ~1 \le a_i \le 10^6~
Sample Input 1
5 2
7 35 13 19 14
Sample Output 1
7
Điểm: 100
Ta có định nghĩa một dãy ngoặc đúng và bậc của dãy ngoặc đó bằng đệ quy như sau:
Nếu ~A~ không có kí tự nào thì ~A~ là một dãy ngoặc đúng bậc ~0~.
Nếu ~A~ là một dãy ngoặc đúng bậc ~a~, ~B~ là một dãy ngoặc đúng bậc ~b~ thì ~(A)~ là một dãy ngoặc đúng bậc ~a + 1~, ~AB~ là một dãy ngoặc đúng bậc ~max(a, b)~.
Cho một xâu ~S~ chỉ gồm các kí tự ~(~ và kí tự ~)~ cùng số ~K~, bạn cần trả lời ~2~ câu hỏi:
~1~. In ra số dãy con liên tiếp của ~S~ là một dãy ngoặc đúng bậc ~K~.
~2~. In ra độ dài của dãy con liên tiếp dài nhất của ~S~ là một dãy ngoặc đúng bậc ~K~.
Input
Gồm hai dòng:
Dòng thứ nhất chứa xâu ~S~ (~1 \leq |S| \leq 10^5~) (trong đó ~|S|~ là độ dài của xâu ~S~).
Dòng thứ hai chứa số ~K~ (~1 \leq K \leq 10^5~).
Output
Dòng thứ nhất in ra câu trả lời của câu hỏi thứ nhất.
Dòng thứ hai in ra câu trả lời của câu hỏi thứ hai, nếu không tồn tại dãy con liên tiếp của ~S~ là dãy ngoặc đúng bậc ~K~ thì in ra -1.
Scoring
Subtask ~1~ (~30\%~ số điểm): ~|S| \leq 5000~.
Subtask ~2~ (~70\%~ số điểm): không có ràng buộc gì thêm.
Sample Input 1
)(())(())(
2
Sample Output 1
3
8
Notes
Có 3 dãy con của ~S~ là dãy ngoặc đúng bậc ~2~: (()), (()), (())(()).
Trong đó, dãy ngoặc đúng bậc ~2~ dài nhất là (())(()).
Lộc có một bàn cờ vua hình chữ nhật có kích thước ~n \times m~, trên bàn cờ đó có ~k~ quân xe đã được đặt sẵn. Mặc dù vậy, Lộc vẫn chưa biết mình sẽ tạo luật chơi mới cho trò "cờ Lộc" này là gì, thay vào đó Lộc đã xác định trước ~q~ vùng trọng điểm chiến lược trên bàn cờ cần phải được bảo vệ kĩ.
Lộc cho rằng một vùng hình chữ nhật được bảo vệ khi và chỉ khi tất cả các hàng hoặc tất cả các cột của vùng ấy, mỗi hàng hoặc mỗi cột đều có ít nhất một quân xe trong vùng canh gác (quân xe có thể tấn công các ô trống trên cùng một hàng hoặc một cột với chính quân xe đó).
Với mỗi vùng trong ~q~ vùng đó, bạn hãy giúp Lộc xác định xem những vùng nào đã được bảo vệ và vùng nào chưa được bảo vệ.
Input
Dòng thứ nhất gồm 4 số nguyên dương ~n, m, k, q~ ~(1 \le n, m \le 10^5,~ ~1 \le k, q \le 2 \cdot 10^5)~ - kích thước hai chiều của bàn cờ, số quân xe ban đầu và số vùng trọng điểm chiến lược.
~k~ dòng tiếp theo, mỗi dòng gồm 2 số nguyên dương ~x, y~ ~(1 \le x \le n,~ ~1 \le y \le m)~ - tọa độ của các quân xe trên bàn cờ của Lộc. Dữ liệu đảm bảo tọa độ của mỗi quân xe trên bàn cờ của Lộc đôi một khác nhau.
~q~ dòng tiếp theo, mỗi dòng gồm 4 số nguyên dương ~x_1, y_1, x_2, y_2~ ~(1 \le x_1 \le x_2 \le n,~ ~1 \le y_1 \le y_2 \le m)~ - tọa độ của ô góc trái trên và góc phải dưới của từng vùng trọng điểm chiến lược.
Output
Gồm ~q~ dòng, dòng thứ ~i~ ~(1 \le i \le q)~ in ra "YES" nếu vùng thứ ~i~ là vùng được bảo vệ, ngược lại in ra "NO".
Scoring
Subtask ~1~ ~(20\%)~:
~q \le 2000~
~n, m \le 200~
~k \le n \cdot m~
Subtask ~2~ ~(20\%)~:
~q \le 2000~
~n, m \le 10^5~
~k \le 2000~
Subtask ~3~ ~(60\%)~: Không có giới hạn thêm.
Sample Input 1
4 3 3 3
1 1
3 2
2 3
2 3 2 3
2 1 3 3
1 2 2 3
Sample Output 1
YES
YES
NO
Một dãy số ~(b_1, b_2, ..., b_m)~ được gọi là có thể tối giản nếu tồn tại một phần tử ~x~ thỏa mãn:
~x~ là duy nhất trong dãy.
Mọi phần tử ~b_1, b_2, ..., b_m~ đều chia hết cho ~x~.
Cho dãy ~a~ gồm ~n~ phần tử ~a_1, a_2, ..., a_n~, hãy đếm số cặp chỉ số ~(l, r)~ ~(1 \le l < r \le n)~ sao cho dãy ~a_l, a_{l+1}, ..., a_r~ là dãy có thể tối giản.
Input
Dòng đầu tiên gồm số nguyên dương ~n~ ~(1 \le n \le 3 * 10^5)~.
Dòng thứ hai gồm ~n~ số nguyên dương ~a_1, a_2, ..., a_n~ ~(1 \le a_i \le 10^9)~.
Output
- Gồm một dòng duy nhất là số dãy tìm được.
Sample Input 1
5
4 3 6 4 2
Sample Output 1
3
Notes
- Các đoạn thỏa mãn là ~[2, 3], [4, 5], [3, 5]~.
Cho dãy số ~A~ gồm ~N~ số nguyên. Bạn cần trả lời ~Q~ truy vấn như sau: cho hai số nguyên ~l~, ~r~, tìm 3 số nguyên ~i, j, k~ ~(l \leq i < j < k \leq r)~ sao cho tích ~a[i] * a[j] * a[k]~ nhỏ nhất.
Input
Dòng đầu tiên gồm hai số nguyên dương ~N~, ~Q~ ~(1 \leq N, Q \leq 2*10^5)~.
Dòng tiếp theo gồm ~N~ số nguyên ~a_1, a_2, ..., a_N~ ~(-10^6 \leq a_i \leq 10^6)~.
~Q~ dòng tiếp theo, mỗi dòng gồm hai số nguyên ~l, r~ ~(1 \leq l \leq r \leq N, r - l \geq 2)~.
Output
In ra ~Q~ dòng, mỗi dòng gồm một số nguyên là tích cần tìm.
Sample Input 1
7 7
-1 -4 -2 5 -3 -3 4
3 6
1 7
4 7
3 6
3 7
2 7
4 7
Sample Output 1
-18
-80
-60
-18
-60
-80
-60
Sample Input 2
6 6
3 2 3 0 -5 0
2 5
1 6
2 6
1 5
3 6
4 6
Sample Output 2
-30
-45
-30
-45
0
0
Cho 1 xâu ~s~ có độ dài n gồm các kí tự
), ( và ?. Gọi ~x~ là số cách thay thế các dấu ? trong xâu để tạo thành 1 dãy ngoặc đúng. In ra ~\min(x, 10)~.
Dãy ngoặc đúng được định nghĩa như sau:
Xâu rỗng là dãy ngoặc đúng
Nếu ~s~ là một dãy ngoặc đúng, ~\texttt{(} + s + \texttt{)}~ cũng là một dãy ngoặc đúng
Nếu ~s_1~ và ~s_2~ là hai dãy ngoặc đúng, ~s_1 + s_2~ cũng là một dãy ngoặc đúng
Input
Dòng đầu tiên chứa 1 số nguyên dương ~t~ (~t \le 10^5~) là số lượng bộ test.
Mỗi bộ test bao gồm duy nhất 1 dòng là xâu ~s~.
Tổng độ dài xâu ~s~ trong các bộ test không vượt quá ~10^5~.
Output
Với mỗi bộ test, in ra ~\min(x, 10)~.
Sample Input 1
10
)(??
)(((
())?
))?)
?(?)
?)?(
???)
((?)
)?()
))?(
Sample Output 1
0
0
0
0
1
0
2
1
0
0