Kỳ thi chọn Đội tuyển HSGQG Quảng Trị năm 2024-2025
Điểm: 100
Việt Anh định nghĩa xâu đối xứng đôi PADBLE là xâu gồm các kí tự in thường ~'a..z'~ trong bảng mã ASCII có độ dài chẵn được ghép thành từ hai xâu con đối xứng có độ dài bằng nhau và có ít nhất hai kí tự khác nhau. Ví dụ xâu ~abacdc~, ~ab~, ~aabb~ là các xâu đối xứng đôi, nhưng xâu ~aaaaabbb~ không phải là xâu đối xứng đôi.
Yêu cầu: Cho xâu ~S~ chỉ chứa các kí tự '~a~' và '~b~', em hãy lập trình giúp Việt Anh tìm độ dài xâu PADBLE lớn nhất và có bao nhiêu xâu con có cùng độ dài lớn nhất đó trong xâu ~S~?
Input
Vào từ tệp văn bản PADBLE.INP chứa xâu ~S~ gồm các kí tự ~a~ và ~b~.
Output
Ghi ra tệp văn bản PADBLE.OUT gồm hai số nguyên là độ dài xâu đối xứng đôi lớn nhất và số xâu có độ dài lớn nhất cách nhau dấu cách. Nếu không có xâu nào thỏa mãn thì in ra ~-1~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~40~ | ~| S | \leq 10^2~ |
| 2 | ~30~ | ~| S | \leq 10^3~ |
| 3 | ~30~ | ~| S | \leq 10^5~ |
Sample Input 1
aaabbaabbbaa
Sample Output 1
4 4
Sample Input 2
aaabbaabbbaaaa
Sample Output 2
6 1
Sample Input 3
aaaaaaaaaaa
Sample Output 3
-1
Notes
Trong ví dụ ~1~, xâu đối xứng đôi độ dài lớn nhất là ~4~ và có ~4~ xâu con thỏa mãn xâu PADBLE là ~aabb~ bắt đầu vị trí số ~2~, ~bbaa~ bắt đầu vị trí số ~4~, ~aabb~ bắt đầu vị trí số ~6~, ~bbaa~ bắt đầu vị trí số ~9~.
Điểm: 100
Cho dãy số nguyên dương ~a_1, a_2, \ldots, a_N~ có ~N~ phần tử. Việt Anh định nghĩa hàm ~f(i, j)~ là tổng của tất cả giá trị ~\frac{a_i \times a_j}{d^2}~ với ~d~ là một ước chung của ~a_i~ và ~a_j~. Ước chung của hai số nguyên dương ~x, y~ là số tự nhiên ~d~ mà ~x, y~ đều chia hết cho ~d~.
Ví dụ dãy ~A = \{2, 1, 4\}~ thì ~f(1, 3) = (2 \times 4)/1^2 + (2 \times 4)/2^2 = 10~ với ~\{1, 2\}~ là các ước chung của 2 và 4, ~f(1, 2) = (2 \times 1)/1^2 = 2~ và ~f(2, 3) = (1 \times 4)/1^2 = 4~.
Tổng GCDS của dãy số chính là tổng tất cả các ~f(i, j)~ định nghĩa ở trên sao cho ~1 \leq i < j \leq N~. Dãy ~A = \{2, 1, 4\}~ có tổng GCDS là ~f(1, 2) + f(1, 3) + f(2, 3) = 16~.
Việt Anh biết các bạn trường THPT Chuyên Lê Quý Đôn học lập trình rất tốt nên đưa ra bài toán như sau: Cho dãy số nguyên dương ~a_1, a_2, \ldots, a_N~ có ~N~ phần tử cần tính tổng GCDS của dãy số. Ngoài ra, Việt Anh còn thực hiện thêm ~Q~ truy vấn, với mỗi truy vấn cho hai số ~(x, y)~ gán phần tử ~a_x = y~. Hãy tính tổng GCDS của dãy số mới.
Yêu cầu: Cho dãy số nguyên dương ~a_1, a_2, \ldots, a_N~ có ~N~ phần tử, thực hiện:
Tính tổng GCDS của dãy số ban đầu;
Trả lời ~Q~ truy vấn, với mỗi truy vấn ~(x, y)~ hãy tính tổng GCDS của dãy số sau khi cập nhật ~a_x = y~.
Input
Dữ liệu vào từ tệp văn bản GCDS.INP có cấu trúc sau:
Dòng đầu tiên chứa hai số nguyên dương ~N~ và ~Q~ (~1 \leq N, Q \leq 5 \times 10^5~);
Dòng thứ 2 ghi dãy ~a_1, a_2, \ldots, a_N~ (~1 \leq a_i \leq 5 \times 10^5~);
~Q~ dòng tiếp theo, mỗi dòng ghi hai số ~x~ và ~y~ biểu thị truy vấn gán ~a_x = y~ (~1 \leq x \leq N~, ~1 \leq y \leq 5 \times 10^5~).
Output
Kết quả ghi ra tệp văn bản GCDS.OUT gồm:
Dòng đầu tiên ghi phần dư của tổng GCDS của dãy số ban đầu khi chia ~10^9 + 7~;
~Q~ dòng tiếp theo, mỗi dòng ghi một số là phần dư của tổng GCDS của dãy khi chia ~10^9 + 7~ tương ứng với thứ tự truy vấn trong tệp dữ liệu vào.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~20\%~ | ~N, Q, a_x, y \le 100~ |
| 2 | ~30\%~ | ~N, Q \le 100~ |
| 3 | ~10\%~ | ~a_x, y \le 12~ |
| 4 | ~20\%~ | ~a_x~ và ~y~ là số nguyên tố |
| 5 | ~20\%~ | Không có ràng buộc nào thêm. |
Sample Input 1
2 2
2 4
1 4
1 3
Sample Output 1
10
21
12
Sample Input 2
4 3
462955 253652 126897 278176
2 5432
1 2314
3 2
Sample Output 2
57273948
41211035
109845881
827916911
Điểm: 100
Nhân dịp khánh thành siêu thị VINCOMPLAZA tại Đông Hà, Việt Anh được bố mẹ dẫn đi chơi tại khu vui chơi có trong siêu thị. Bạn ấy rất thích thú với các trò chơi ở đây, đặc biệt là trò chơi mang tên "G_SCORES" với hệ thống tính điểm vô cùng thú vị.
G_SCORES là trò chơi mới được các nhà phát triển tạo ra ~N~ màn chơi, màn chơi thứ ~i~ có cấp độ là ~i~. Hệ thống điểm thưởng cho các cấp độ của trò chơi được thiết lập như sau:
Cấp độ ~i~ có điểm thưởng là số nguyên dương ~s_i~ có giá trị từ ~1~ đến ~N~. Các cấp độ được sắp xếp theo độ khó tăng dần ~(s_1 \leq s_2 \leq \ldots \leq s_n)~;
Để đảm bảo người chơi vượt qua nhiều cấp độ sẽ được xếp hạng cao hơn, các nhà phát triển thiết lập quy tắc: Với một số ~k~ ~(2 \leq k \leq N)~ bất kỳ, tổng số điểm của ~k~ màn chơi phải lớn hơn tổng số điểm của mọi lần mà có số màn chơi ít hơn ~k~.
Yêu cầu: Cho ~N~ màn chơi, hỏi có bao nhiêu cách thiết lập hợp lệ để các nhà phát triển thiết lập hệ thống điểm cho các cấp độ thỏa mãn những điều kiện nêu trên?
Input
Vào từ tệp văn bản SCORES.INP có cấu trúc sau:
Dòng đầu tiên chứa một số nguyên ~T~ ~(1 \leq T \leq 5)~ là số lượng bộ tests;
~T~ dòng tiếp theo, dòng thứ ~i~ chứa số nguyên ~N (2 \leq N \leq 5000)~ là số màn chơi.
Output
Ghi ra vào tệp SCORES.OUT gồm có ~T~ dòng, dòng thứ ~i~ theo thứ tự ghi phần dư của số cách thiết lập hệ thống điểm hợp lệ khi chia ~10^9 + 7~
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~20\%~ | ~T = 1, N \leq 15~ |
| 2 | ~30\%~ | ~T = 1, 15 \lt N \leq 35~ |
| 3 | ~20\%~ | ~35 \lt N \leq 100~ |
| 4 | ~20\%~ | ~100 \lt N \leq 1000~ |
| 5 | ~10\%~ | Không có ràng buộc gì thêm |
Sample Input 1
3
2
3
4
Sample Output 1
3
7
16
Notes
Ở ví dụ trên với ~N = 3~ ta có ~7~ dãy ~s_i~ tương ứng như sau:
~1 \space 1 \space 1~
~1 \space 2 \space 2~
~1 \space 3 \space 3~
~2 \space 2 \space 2~
~2 \space 2 \space 3~
~2 \space 3 \space 3~
~3 \space 3 \space 3~
Điểm: 100
An rất thích sưu tập tem và An đã sưu tập được nhiều con tem quý. Tại một buổi trưng bày các con tem cổ của những người sưu tập tem trong thành phố, An phát hiện ra một con tem cổ mà An rất thích và đã mất rất nhiều công sức tìm kiếm lâu nay. An muốn mua lại con tem đó nhưng chủ nhân của con tem không bán mà chỉ đồng ý trao đổi bằng những con tem mà An đang có.
Bộ sưu tập của An có ~N~ con tem, đánh số từ ~1~ đến ~N~. Con tem thứ ~i~ có giá trị ~C_i~ với ~i = 1, 2, \ldots, N~. Các con tem có giá trị bằng nhau được xem là cùng một loại. Chủ nhân của con tem mà An muốn đổi yêu cầu An phải đổi bằng một số con tem và tổng giá trị của các con tem đó phải lớn hơn hoặc bằng ~P~.
An rất muốn sở hữu con tem cổ nhưng cũng cân nhắc cách đổi sao cho giữ lại cho mình nhiều loại tem khác nhau nhất và tổng giá trị các con tem đem trao đổi càng nhỏ càng tốt.
Yêu cầu: Bạn hãy tìm cách trao đổi giúp An có được con tem như mong muốn.
Input
Dữ liệu vào từ tệp văn bản EXCHANGE.INP gồm:
Dòng đầu tiên chứa hai số nguyên ~N~ và ~P~ (~1 \leq N, P \leq 6 \times 10^4~);
Dòng tiếp theo chứa ~N~ số chuyên không âm ~C_1, C_2, \ldots, C_N~ và ~P \leq C_1 + C_2 + \cdots + C_N \leq 2 \times P~.
Các số trên cùng một dòng cách nhau bằng dấu cách.
Output
Kết quả ghi ra tệp văn bản EXCHANGE.OUT gồm:
Dòng thứ nhất ghi hai số nguyên dương ~D~ và ~S~ (~S \geq P~) với ~D~ là số lượng loại tem khác nhau còn lại sau khi trao đổi và ~S~ là tổng giá trị các con tem đem ra trao đổi;
Dòng thứ hai ghi ~K~ số nguyên ~C_{i_1}, C_{i_2}, \ldots, C_{i_K}~ là giá trị các con tem đem ra trao đổi theo thứ tự không giảm.
Các số trên một dòng ghi cách nhau bằng dấu cách.
Nếu chỉ đúng giá trị ~D~ thì được ~20\%~ số điểm của test đó.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~20\%~ | ~n \leq 20~ |
| 2 | ~25\%~ | ~C_i \neq C_j~ với mỗi cặp ~(i, j)~ (~1 \leq i \text{ < } j \leq N~) |
| 3 | ~20\%~ | ~N, P \leq 5 \times 10^3~ |
| 4 | ~35\%~ | Không có ràng buộc gì thêm |
Sample Input 1
8 21
5 5 5 0 7 4 7 9
Sample Output 1
4 21
4 5 5 7
Sample Input 2
7 100
90 2 2 3 3 6 6
Sample Output 2
3 101
2 3 6 90
Notes
Ở test ví dụ ~1~, ta có hai cách để đổi, ngoài test ví dụ ta cũng có thể dùng các con tem ~(4, 5, 5, 7)~ để đổi
Ở test ví dụ ~2~, để còn lại 3 loại team ~(2, 3, 6)~, cần phải đổi các con tem với tổng là 101
Điểm: 100
Trong thời gian chờ vào tiết học, An và Lạc cùng nhau chơi một trò chơi đơn giản. An lấy một tờ giấy và học sinh hình chữ nhật kẻ ô vuông có chiều rộng ~W~, chiều cao ~H~ và vẽ một số điểm lên tờ giấy đó. Có thể xem góc dưới bên trái của tờ giấy có tọa độ ~(0, 0)~ và góc trên bên phải có tọa độ ~(W, H)~. Các điểm có thể vẽ trùng nhau nhưng được tính như các điểm phân biệt. Lạc lấy ra một mảnh giấy hình chữ nhật có chiều rộng ~w~, chiều cao ~h~ và hai bạn tìm cách đặt mảnh giấy này lên tờ giấy sao cho các cạnh của mảnh giấy song song với các biên của tờ giấy đã vẽ các điểm, chiều rộng và chiều cao mảnh giấy tương ứng với chiều rộng và chiều cao của tờ giấy và mảnh giấy phủ nhiều điểm nhất có thể. Các điểm nằm trên biên của mảnh giấy cũng được xem là bị phủ.
An, Lạc đã vào lớp. Bạn hãy tiếp tục trò chơi khi tờ giấy và mảnh giấy có kích thước lớn hơn.
Yêu cầu: Cho ~n~ điểm và kích thước ~w, h~ của mảnh giấy, hãy tìm số điểm lớn nhất bị phủ bởi mảnh giấy hình chữ nhật đó.
Input
Dữ liệu vào từ tệp văn bản RECTPOINTS.INP gồm:
Dòng đầu chứa ba số nguyên ~n, w, h~ (~1 \leq n \leq 10^5, 1 \leq w, h \leq 10^8~);
~n~ dòng tiếp theo, dòng thứ ~i~ chứa hai số nguyên ~x_i, y_i~ là tọa độ của điểm thứ ~i~ được vẽ trên tờ giấy (~1 \leq x_i, y_i \leq 10^8~).
Các số trên mỗi dòng được ghi cách nhau dấu cách.
Output
Kết quả ghi ra tệp văn bản RECTPOINTS.OUT gồm một dòng ghi một số là số lượng điểm lớn nhất bị phủ bởi mảnh giấy hình chữ nhật.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~10\%~ | ~n \leq 10^2~ và ~x_i, y_i, w, h \leq 10^2~ |
| 2 | ~25\%~ | ~n \leq 10^3~ và ~x_i, y_i, w, h \leq 10^8~ |
| 3 | ~15\%~ | ~n \leq 10^5~, ~x_i, y_i, w, h \leq 10^3~, một trong các hình chữ nhật kết quả có góc trên bên phải là một trong các điểm đã cho |
| 4 | ~15\%~ | ~n \leq 10^5~, ~x_i, y_i, w, h \leq 10^5~, một trong các hình chữ nhật kết quả có góc trên bên phải là một trong các điểm đã cho |
| 5 | ~35\%~ | Không có ràng buộc gì thêm |
Sample Input 1
6 2 3
1 1
3 1
2 2
3 3
5 3
3 5
Sample Output 1
4
Sample Input 2
10 8 8
8 9
20 14
3 9
7 8
3 4
7 8
10 19
6 11
5 10
8 2
Sample Output 2
7
Điểm: 100
Quốc gia Byteland xinh đẹp có ~N~ thành phố đánh số từ ~1~ đến ~N~. Có ~M~ tuyến đường một chiều nối giữa hai thành phố khác nhau, đánh số từ ~1~ đến ~M~. Có thể có nhiều hơn một tuyến đường cùng một chiều nối giữa hai thành phố.
Chính quyền Byteland chuẩn bị kế hoạch sửa chữa các tuyến đường. Tuyến đường trong thời gian sửa chữa sẽ dừng hoạt động. Một câu hỏi đặt ra cho chính quyền lúc này là: "Có thể đi từ thành phố ~A~ đến thành phố ~B~ và từ ~B~ quay lại thành phố ~A~ được hay không khi dừng hoạt động của một trong các tuyến đường của quốc gia?". Bởi sẽ có nhiều cặp thành phố cần có sự kết nối giao thông giữa chúng trong thời gian thi công các tuyến đường, bạn hãy giúp chính quyền Byteland trả lời các câu hỏi đó.
Input
Dữ liệu vào từ tệp văn bản CONNECT.INP gồm:
Dòng đầu chứa hai số nguyên ~N, M~ (~2 \leq N \leq 2000~, ~1 \leq M \leq 10^5~);
~M~ dòng tiếp theo, mỗi dòng chứa hai số nguyên ~u, v~ (~1 \leq u, v \leq N~) mô tả một tuyến đường một chiều nối từ thành phố ~u~ đến thành phố ~v~;
Dòng tiếp theo chứa số nguyên ~Q~ (~0 \leq Q \leq 10^5~):
Nếu ~Q \neq 0~ thì ~Q~ dòng tiếp theo mỗi dòng chứa hai số nguyên ~A, B~ (~1 \leq A, B \leq N~) mô tả một câu hỏi;
Nếu ~Q = 0~ thì không chứa gì thêm, khi đó bạn sẽ trả lời tất cả các câu hỏi tương ứng với các cặp có thứ tự: ~(1,1)~; ~(1,2)~; ~(1,3)~; ...; ~(1,N)~; ~(2,2)~; ~(2,3)~; ...; ~(N,N)~.
Các số trên một dòng cách nhau đúng một dấu cách.
Output
Kết quả ghi ra tệp văn bản CONNECT.OUT:
Với mỗi câu hỏi tương ứng với một cặp thành phố ~A, B~ bạn trả lời theo một trong các giá trị sau:
~0~: Nếu không dừng hoạt động tuyến đường nào mà vẫn không có đường đi cho ít nhất một trong hai hướng (từ ~A~ đến ~B~ hoặc từ ~B~ đến ~A~);
~M + 1~: Nếu dừng hoạt động của bất kỳ tuyến đường nào thì cũng có đường đi từ ~A~ đến ~B~ và từ ~B~ quay lại ~A~;
~E~: Là một số trong khoảng từ ~1~ đến ~M~ là số hiệu tuyến đường mà khi dừng hoạt động tuyến đường đó thì sẽ không có đường đi cho ít nhất một trong hai hướng. Nếu có nhiều tuyến đường như vậy thì ghi ra tuyến đường có số hiệu nhỏ nhất.
Để ghi ra các giá trị này bạn thực hiện theo yêu cầu sau:
Gọi ~r_1, r_2, \dots, r_k~ là các giá trị trả lời cho ~Q~ câu hỏi (~K = Q~) trong trường hợp ~Q \neq 0~, nếu ~Q = 0~ thì ~K = \frac{N \times (N+1)}{2}~;
Kết quả ghi ra tệp gồm một dòng ghi một số là phần dư của số nguyên ~P~ khi chia cho ~10^9 + 7~ với: $$P = r_1 \times B^{K-1} + r_2 \times B^{K-2} + r_3 \times B^{K-3} + \dots + r_K \times B^0$$ trong đó ~B = 2 \times 10^5~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~15\%~ | ~N \leq 200~, ~M \leq 1000~, ~Q \leq 500~ và ~Q \neq 0~ |
| 2 | ~15\%~ | ~N \leq 2000~, ~M \leq 10^5~, ~Q \leq 10^5~ và kết quả trả lời các câu hỏi chỉ một trong hai giá trị: ~0~ hoặc ~M+1~ |
| 3 | ~20\%~ | ~N \leq 500~, ~M \leq 8000~, ~Q \leq 10^5~ |
| 4 | ~25\%~ | ~N \leq 2000~, ~M \leq 10^5~, ~Q \leq 10^4~, ~Q \neq 0~ |
| 5 | ~25\%~ | Không có ràng buộc gì thêm |
Sample Input 1
6 11
1 4
4 3
3 5
5 1
1 3
3 6
5 6
6 2
4 2
5 1
3 5
0
Sample Output 1
575589257
Sample Input 2
8 17
5 2
6 5
4 6
4 8
4 3
3 1
2 7
7 4
5 4
8 7
8 3
3 6
6 1
2 4
1 5
1 5
5 2
4
4 6
8 1
5 2
6 7
Sample Output 2
995598902
Notes
Ở test ví dụ thứ nhất:
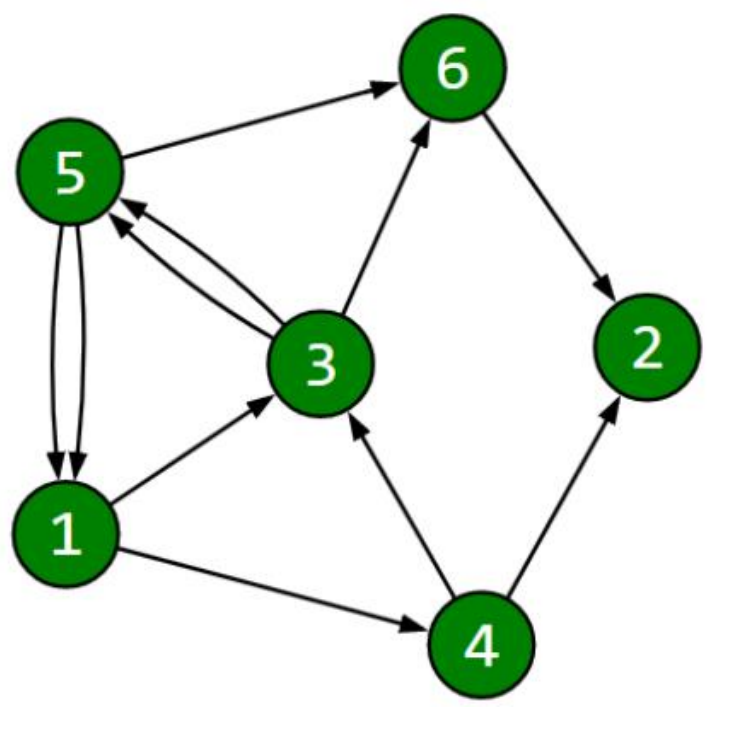
Câu hỏi ~(1, 6)~: Không có đường đi từ 6 về 1 trong khi không dừng hoạt động tuyến đường nào.
Câu hỏi ~(1, 3)~: Dừng hoạt động bất kỳ tuyến đường nào thì cũng có đường đi theo cả hai hướng giữa ~1~ và ~3~.
Câu hỏi ~(4, 5)~: Khi dừng hoạt động tuyến đường từ ~1~ đến ~4~ (số hiệu ~1~) thì sẽ không có đường đi từ ~5~ đến ~4~.
Dãy kết quả tương ứng: 12 0 12 1 12 0 12 0 0 0 0 12 1 12 0 12 1 0 12 0 12.
Ở test ví dụ thứ hai:
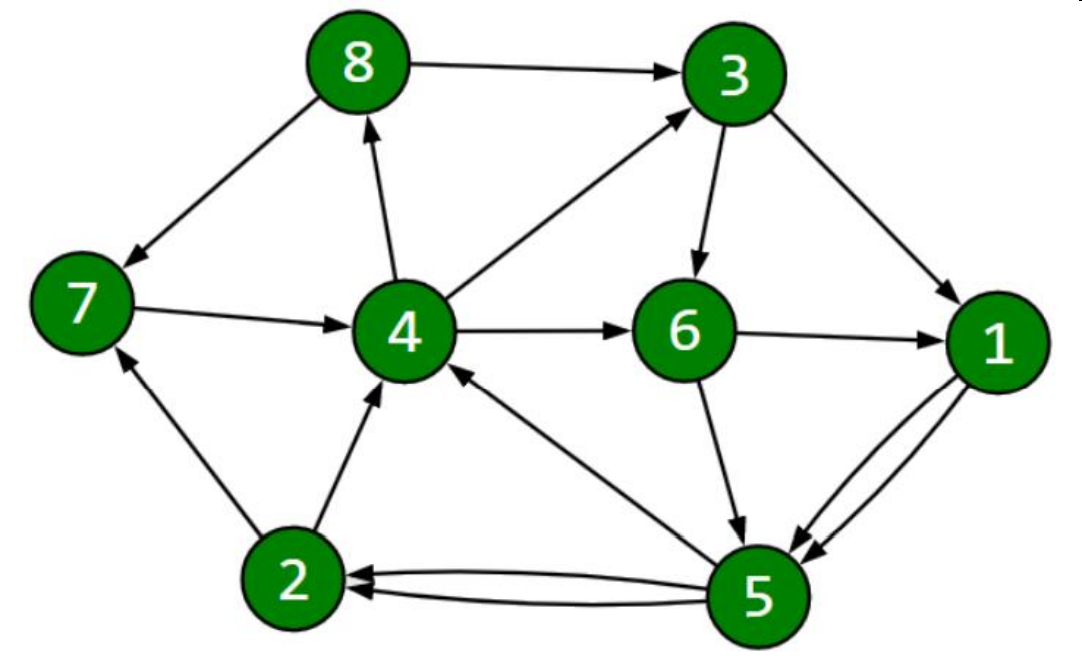
Câu hỏi ~(8, 1)~: Nếu dừng hoạt động tuyến đường từ ~4~ đến ~8~ thì sẽ không có đường đi từ ~1~ đến ~8~.
Câu hỏi ~(6, 7)~: Nếu dừng hoạt động tuyến đường từ ~7~ đến ~4~ thì sẽ không có đường đi từ ~7~ đến ~6~.
Dãy kết quả tương ứng: 18 4 18 8.