Educational Centroid Decomposition Contest
Điểm: 100
Bạn được cho ~1~ cây gồm ~n~ đỉnh. Việc của bạn là tìm ~\texttt{centroid}~ của cây, đỉnh mà nếu lấy nó là gốc của cây, mọi cây con đều có kích thước không quá ~\lfloor \frac{n}{2} \rfloor~.
Input
Dòng đầu chứa số nguyên ~n~ (~1 \le n \le 2 \times 10^5~), số lượng đỉnh của cây. Các đỉnh được đánh số lần lượt từ ~1~, ~2~, ~3~, ~\cdots~, ~n~.
Sau đó là ~n - 1~ dòng là các cạnh của cây. Mỗi dòng gồm ~2~ số nguyên ~a~ và ~b~ (~1 \le a, b \le n~) tương ứng là cạnh giữa ~2~ đỉnh ~a~ và ~b~ trên cây.
Output
In ra chỉ số đỉnh của ~\texttt{centroid}~ của cây. Nếu có nhiều đỉnh thoả mãn thì có thể in đỉnh bất kỳ.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| ~1~ | ~50\%~ | ~1 \leq n \leq 5 \times 10^3~ |
| ~2~ | ~50\%~ | Không có ràng buộc gì thêm |
Sample Input 1
7
1 2
2 3
3 4
3 5
2 6
6 7
Sample Output 1
2
Sample Input 2
10
4 1
6 5
7 2
6 3
1 7
2 10
10 9
3 8
8 9
Sample Output 2
10
Notes
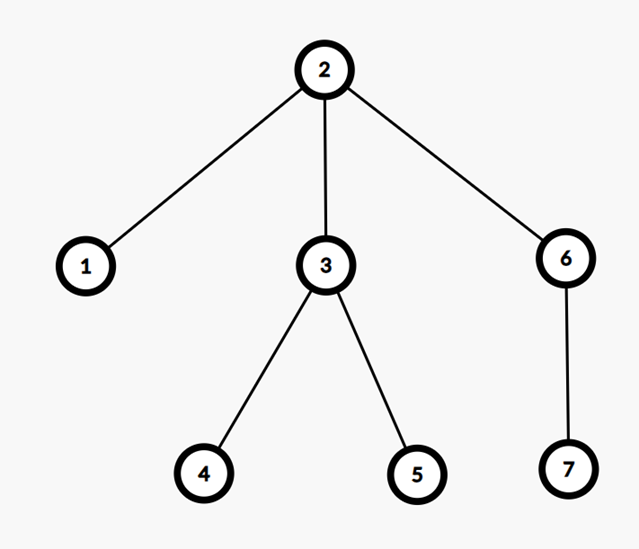
Trong test ví dụ đầu tiên, đỉnh ~2~ là ~\texttt{centroid}~ của cây bởi:
Lấy đỉnh ~2~ là gốc của cây:
— Những cây con có kích thước là ~1~: ~1~, ~4~, ~5~, ~7~.
— Những cây con có kích thước là ~2~: ~6~.
— Những cây con có kích thước là ~3~: ~3~.
Mọi cây con đều có kích thước không quá ~\lfloor \frac{n}{2} \rfloor = \lfloor \frac{6}{2} \rfloor = 3~.
Điểm: 100
Cho một cây ~N~ đỉnh, hãy đếm số lượng đường đi phân biệt có độ dài trong khoàng ~[k_1,k_2]~.
Input
Dòng đầu gồm ~3~ số ~N,k_1,k_2~ ~(1\le k_1\le k_2\le N\le 2*10^5)~
~N-1~ dòng tiếp theo, mỗi dòng gồm hai số thể hiện cạnh trên cây.
Output
- Gồm ~1~ số là số lượng đường đi phân biệt
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| ~1~ | ~30\%~ | ~N\le5000~ |
| ~2~ | ~20\%~ | ~k_1=k_2~ |
| ~3~ | ~50\%~ | Không có ràng buộc gì thêm |
Sample Input 1
5 2 3
1 2
2 3
3 4
3 5
Sample Output 1
6
Điểm: 100
Xenia — một lập trình viên, có một cái cây gồm ~n~ đỉnh. Các đỉnh được đánh số từ ~1~ tới ~n~ và có màu xanh hoặc đỏ. Ban đầu, đỉnh ~1~ được tô màu đỏ, trong khi các đỉnh còn lại được tô màu xanh.
Khoảng cách giữa hai đỉnh ~u~ và ~v~ được định nghĩa là số cạnh trên đường đi ngắn nhất từ ~u~ tới ~v~.
Xenia có các truy vấn thuộc ~1~ trong ~2~ loại sau:
~1\ i~: tô đỉnh ~i~ từ màu xanh thành màu đỏ.
~2\ i~: In khoảng cách ngắn nhất từ đỉnh ~i~ tới một đỉnh đang có màu đỏ (nếu đỉnh ~i~ đang được tô màu đỏ thì đáp án sẽ là ~0~).
Vì Xenia không thể giải được bài toán trên nên bạn hãy giúp anh ấy giải bài toán này nhé!
Input
Dòng đầu tiên gồm hai số nguyên dương ~n~ và ~m~ (~2 \leq n \leq 10^5~, ~1 \leq m \leq 10^5~), lần lượt là số đỉnh của cây và số truy vấn của bài toán.
Mỗi dòng trong số ~n - 1~ dòng tiếp theo chứa hai số nguyên dương ~a_i~ và ~b_i~ (~1 \leq a_i, b_i, \leq n~, ~a_i \neq b_i~) thể hiện một cạnh của cây.
Mỗi dòng trong số ~m~ dòng tiếp theo gồm 2 số có dạng ~1\ i~ hoặc ~2\ i~ (~1 \leq i \leq n~) thể hiện một truy vấn thuộc ~2~ loại truy vấn ở trên.
Dữ liệu đảm bảo lúc thực hiện truy vấn ~1~ thì đỉnh ~i~ đang có màu xanh.
Output
Với mỗi truy vấn thuộc loại ~2~ thì in ra câu trả lời cho truy vấn đó.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | ~20~ | ~n, q \leq 5000~ |
| ~2~ | ~30~ | Mọi truy vấn ~1~ diễn ra trước truy vấn ~2~ |
| ~3~ | ~50~ | Không có ràng buộc gì thêm |
Sample Input 1
3 3
1 2
2 3
2 3
1 2
2 3
Sample Output 1
2
1
Sample Input 2
5 4
1 2
2 3
2 4
4 5
2 1
2 5
1 2
2 5
Sample Output 2
0
3
2
Notes
Ở test ví dụ đầu tiên:
Trong truy vấn loại ~2~ đầu tiên, đỉnh màu đỏ gần với đỉnh ~3~ nhất là đỉnh ~1~ nên khoảng cách tới đỉnh màu đỏ gần nhất là ~d(3, 1) = 2~.
Trong truy vấn loại ~2~ tiếp theo, đỉnh màu đỏ gần với đỉnh ~3~ nhất là đỉnh ~2~ nên khoảng cách tới đỉnh màu đỏ gần nhất là ~d(3, 2) = 1~.
Ở test ví dụ thứ hai:
Trong truy vấn loại ~2~ đầu tiên, đỉnh ~1~ đã được tô màu đỏ nên khoảng cách của đỉnh này tới đỉnh màu đỏ gần nhất là ~d(1, 1) = 0~.
Trong truy vấn loại ~2~ tiếp theo, đỉnh màu đỏ gần với đỉnh ~5~ nhất là đỉnh ~1~ nên khoảng cách tới đỉnh màu đỏ gần nhất là ~d(5, 1) = 3~.
Trong truy vấn loại ~2~ cuối cùng, đỉnh màu đỏ gần với đỉnh ~5~ nhất là đỉnh ~2~ nên khoảng cách tới đỉnh màu đỏ gần nhất là ~d(5, 2) = 2~.
Điểm: 100
Vương quốc Alpha là một tiểu vương quốc mới được thành lập và đang trên đà phát triển. Quốc vương của họ - Aleck - quyết định chia nhỏ vương quốc thành ~n~ tỉnh thành để dễ dàng kiểm soát hơn. Để tiết kiệm chi phí, nhà vua chỉ cho xây dưng ~n - 1~ con đường kết nối giữa ~2~ tỉnh thành khác nhau, tuy nhiên vẫn phải đảm bảo ~2~ tỉnh thành bất kỳ phải đến được với nhau.
Nhà vua đang gấp rút đề cử ra ~n~ người giám sát, mỗi người sẽ có nhiệm vụ giám sát hoạt động của ~1~ tỉnh thành. Hơn nữa, nhà vua muốn gán cấp bậc của mỗi người giám sát là ~1~ chữ cái từ 'A' đến 'Z' biểu thị cho mức độ quan trọng của tỉnh thành đó. Bậc 'A' là cao nhất, còn bậc 'Z' là thấp nhất.
Việc gán cấp bậc cho mỗi người giám sát còn phải đảm bảo được rằng: Nếu tồn tại ~2~ thành phố có người giám sát là cùng bậc, thì đường đi kết nối giữa ~2~ thành phố đó phải đi qua ít nhất ~1~ thành phố có người giám sát có cấp bậc cao hơn. Điều này cho thấy được tầm quan trọng của những người giám sát bậc cao.
Đề xuất cho nhà vua Aleck ~1~ cách để thực hiện việc đó, hoặc thông báo cho nhà vua biết điều đó là bất khả thi.
Input
Dòng ~1~: Gồm một số nguyên ~n~ ~(1 \le n \le 10^5)~ là số lượng tỉnh thành của vương quốc Alpha.
~n - 1~ dòng tiếp theo, mỗi dòng chứa ~2~ số nguyên ~a, b~ ~(1 \le a, b \le n; a \ne b)~ là một con đường ~2~ chiều kết nối giữa ~2~ tỉnh thành ~a~ và ~b~.
Output
Nếu có ~1~ cách thỏa mãn, in ra ~n~ chữ cái in hoa, chữ cái thứ ~i~ đại diện cho cấp bậc của người giám sát cho tỉnh thành ~i~.
Nếu không, in ra 'Impossible!'.
Scoring
Subtask ~1~ ~(30\%~ số điểm~):~ Mỗi tỉnh thành chỉ được kết nối với tối đa ~2~ tỉnh thành khác.
Subtask ~2~:~(30\%~ số điểm~):~ Khoảng cách tối đa giữa ~2~ tỉnh thành bất kỳ không vượt quá ~50~.
Subtask ~3~:~(40\%~ số điểm~):~ Không có điều kiện gì thêm.
Sample Input 1
4
1 2
1 3
1 4
Sample Output 1
A B B B
Sample Input 2
10
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10
Sample Output 2
D C B C A D C B C D
Điểm: 100
Kết hợp với IOI, thành phố Pattaya sẽ tổ chức cuộc đua: Olympic quốc tế về đua tốc độ (IOR) ~2011~.
Là nhà tổ chức, chúng ta phải tìm ra vòng đua tốt nhất cho cuộc thi tốc độ này.
Ở vùng Pattaya ~-~ Chonburi, có ~N~ thành phố được nối với nhau bởi mạng gồm ~N - 1~ đường cao tốc. Mỗi đường cao tốc đều cho phép đi theo cả hai chiều nối hai thành phố phân biệt và có độ dài đo bởi kilomet là số nguyên. Ngoài ra có đúng một đường đi giữa cặp hai thành phố bất kỳ. Nghĩa là, có đúng một cách đi từ một thành phố này đến một thành phố khác dọc theo dãy các đường cao tốc không qua bất cứ thành phố nào quá một lần.
IOR có qui tắc đặc biệt đòi hỏi vòng đua phải dài đúng ~K~ kilomet, bắt đầu và kết thúc ở hai thành phố phân biệt. Rõ ràng là không có đường cao tốc (và vì thế cũng không có thành phố) nào có thể được sử dụng quá một lần trên vòng đua để ngăn ngừa đụng độ. Để cực tiểu ảnh hưởng đến giao thông, vòng đua phải chứa một số ít nhất đường cao tốc có thể.
Yêu cầu: Bạn hãy cho biết số lượng đường cao tốc nhỏ nhất trên vòng đua hợp qui tắc có độ dài đúng bằng ~K~. Nếu không tìm được vòng đua như vậy, kết quả sẽ là ~- 1~.
Input
- Dòng đầu ghi số ~N~, ~K~.
- ~N - 1~ dòng tiếp theo mỗi dòng ghi ~3~ số ~u~, ~v~, ~l~ -- đường cao tốc nối thành phố ~u~ và ~v~, độ dài ~l~ ~(l \le 10^{6})~.
Output
~1~ số nguyên duy nhất là kết quả của bài toán.
Giới hạn
- ~1 \leq N \leq 2 \times 10^{5}~
- ~1 \leq K \leq 10^{6}~
Sample Input 1
4 3
0 1 1
1 2 2
1 3 4
Sample Output 1
2
Sample Input 2
3 3
0 1 1
1 2 1
Sample Output 2
-1
Sample Input 3
11 12
0 1 3
0 2 4
2 3 5
3 4 4
4 5 6
0 6 3
6 7 2
6 8 5
8 9 6
8 10 7
Sample Output 3
2
Điểm: 100
ZS the Coder có một cây lớn và được biểu diễn dưới dạng đồ thị vô hướng liên thông của ~n~ đỉnh được đánh số từ ~0~ đến ~n - 1~ và ~n - 1~ cạnh nối giữa chúng. Trên mỗi cạnh có một chữ số khác không.
Một ngày nọ, ZS the Coder cảm thấy chán chường và quyết định điều tra một số tính chất của cây. Anh ấy chọn một số nguyên dương ~M~, sao cho ~M~ là số nguyên tố cùng nhau với ~10~, tức là ~GCD(M, 10) = 1~.
ZS xem một cặp đỉnh có thứ tự (~u, v~) là thú vị khi nếu anh ấy đi theo đường đi ngắn nhất từ đỉnh ~u~ đến đỉnh ~v~ và viết tất cả các chữ số mà anh ấy gặp trên con đường của mình theo thứ tự, anh ấy sẽ được một biểu diễn thập phân của một số nguyên chia hết cho ~M~.
Cụ thể, ZS xem một cặp đỉnh có thứ tự (~u, v~) là thú vị nếu các điều kiện sau đúng:
Gọi ~a_1 = u, a_2, ..., a_k = v~ là chuỗi các đỉnh trên đường đi ngắn nhất theo thứ tự từ ~u~ đến ~v~;
Gọi ~d_i~ (~1 \leq i < k~) là chữ số được viết trên cạnh giữa các đỉnh ~a_i~ và ~a_{i + 1}~;
Số nguyên dương ~\overline{d_1 d_2 d_3 ... d_{k-1}} = \sum_{i=1}^{k-1}d_i \cdot 10^{k-1-i}~ chia hết cho ~M~.
Hãy giúp ZS the Coder tìm số lượng cặp đỉnh thú vị!
Input
Dòng đầu tiên chứa hai số nguyên dương ~n~ và ~M~ (~2 \leq n \leq 100000, 1 \leq M \leq 10^9, gcd(M, 10) = 1~) — số đỉnh và số mà ZS đã chọn.
Trong ~n-1~ dòng tiếp theo, dòng thứ ~i~ chứa 3 số nguyên ~u_i, v_i, w_i~ biểu diễn một cạnh nối đỉnh ~u_i~ và ~v_i~ với chữ số ~w_i~ viết trên đó(~0 \leq u_i, v_i \leq n, 1 \leq w_i \leq 9~).
Output
Ghi ra một số nguyên duy nhất là số lượng cặp đỉnh thú vị.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | ~40~ | ~n \leq 2000~ |
| ~2~ | ~60~ | Không có ràng buộc gì thêm |
Sample Input 1
6 7
0 1 2
4 2 4
2 0 1
3 0 9
2 5 7
Sample Output 1
7
Sample Input 2
5 11
1 2 3
2 0 3
3 0 3
4 3 3
Sample Output 2
8
Điểm: 100
Một mạng truyền tin có ~N~ máy tính, các máy tính được đánh số từ ~1~ đến ~N~. Có ~N - 1~ dây cáp, được đánh số từ ~1~ đến ~N - 1~. Dây cáp thứ ~i~ nối máy tính ~u_i~ với máy tính ~v_i~ và có giới hạn truyền tải ~w_i~. Các dây cáp bảo đảm từ một máy tính bất kì có thể truyền tin đến tất cả các máy tính còn lại theo dây cáp trực tiếp giữa chúng hoặc thông qua đường truyền tin đi qua một số máy tính và dây cáp nào đó. Khi hai máy tính truyền tin cho nhau, chúng sẽ luôn sử dụng đường truyền tin sao cho không sử dụng dây cáp nào quá một lần. Độ lớn của gói tin truyền đi phải không lớn hơn giới hạn truyền tải của mọi dây cáp mà nó sử dụng. Chi phí để truyền một gói tin giữa hai máy tính bằng kích thước của gói tin nhân với bình phương số lượng dây cáp trên đường truyền tin.
Người ta muốn chọn ra một máy tính ~r~ để làm máy chủ. Khi đó, máy tính ~r~ sẽ truyền tin đến tất cả các máy tính khác. Vì phải dự trù cho mọi trường hợp, ta cần phải xét chi phí truyền tin tối đa. Chi phí truyền tin tối đa giữa máy tính ~r~ và máy tính ~x~ là ~C_{min}(r, x) \times (D(r, x))^2~ với ~C_{min}(r, x)~ là giới hạn truyền tải nhỏ nhất trong số các giới hạn truyền tải của các dây cáp trên đường truyền tin giữa máy tính ~r~ và máy tính ~x~, ~D(r, x)~ là số dây cáp trên đường truyền tin giữa máy tính ~r~ và máy tính ~x~. Chi phí vận hành mạng là tổng của chi phí truyền tin tối đa giữa máy tính ~r~ và tất cả các máy tính khác.
~\textbf{Yêu cầu}~: Với mỗi ~r = 1, 2, \ldots, N~, hãy tính chi phí vận hành mạng nếu chọn máy tính ~r~ làm máy chủ.
Input
Vào từ file văn bản NETW.INP:
Dòng đầu chứa một số nguyên ~N~ là số lượng máy tính ~(1 \leq N \leq 10^5)~.
Dòng thứ ~i~ trong số ~N - 1~ dòng tiếp theo chứa ba số nguyên ~u_i, v_i~ và ~w_i~ cho biết có một dây cáp nối máy tính ~u_i~ với máy tính ~v_i~ và có giới hạn truyền tải là ~w_i~ ~(1 \leq u_i, v_i \leq N; 1 \leq w_i \leq 10^9)~.
Các số trên cùng một dòng cách nhau bởi dấu cách.
Output
Ghi ra file văn bản NETW.OUT:
- Gòm ~N~ dòng, trong đó dòng thứ ~r~ chứa một số nguyên là phần dử của chi phí vận hành mạng nếu chọn máy tính ~r~ làm máy chủ trong phép chia cho ~998244353~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~16\%~ | ~N \leq 5000~. |
| 2 | ~12\%~ | ~w_i \leq 2~ và luôn có dây cáp nối giữa máy tính ~i~ và máy tính ~i + 1, \forall i = 1, 2, \ldots, N - 1~. |
| 3 | ~20\%~ | ~w_i = 1, \forall i = 1, 2, \ldots, N - 1~. |
| 4 | ~16\%~ | ~w_i \leq 1000, \forall i = 1, 2, \ldots, N - 1~. |
| 5 | ~16\%~ | Luôn có dây cáp nối giữa máy tính ~i~ và máy tính ~i + 1, \forall i = 1, 2, \ldots, N - 1~. |
| 6 | ~20\%~ | Không có ràng buộc gì thêm. |
Sample Input 1
7
1 2 3
1 3 2
2 4 2
2 6 1
4 5 1
4 7 2
Sample Output 1
44
26
85
35
43
36
73
Điểm: 100
Làng X có ~N~ khu dân cư được nối với nhau bởi ~N-1~ con đường, sao cho tồn tại đường đi giữa 2 khu dân cư bất kỳ. Để đáp ứng nhu cầu cấp điện cho các hộ dân, chính quyền muốn xây 2 trạm biến áp tại 2 trong số ~N~ khu dân cư này. Vì lý do phong thủy, họ muốn chọn 2 khu dân cư sao cho khoảng cách giữa chúng (số con đường trên đường đi ngắn nhất) là một số nguyên tố.
Hãy giúp chính quyền biết, nếu chọn ngẫu nhiên 2 khu dân cư thì xác suất 2 khu dân cư này phù hợp để xây trạm biến áp là bao nhiêu?
Input
Dòng đầu tiên chứa 1 số nguyên dương ~N~ (~2 \le N \le 50000~).
~N-1~ dòng tiếp theo, mỗi dòng chứa 2 số nguyên dương ~u~ và ~v~ (~1 \le u,v \le N~, ~u \neq v~) cho biết có con đường nối 2 khu dân cư ~u~ và ~v~.
Dữ liệu đầu vào đảm bảo tồn tại đường đi giữa 2 khu dân cư bất kỳ.
Output
In ra 1 số thực: xác suất chọn ra 2 khu dân cư phù hợp để xây trạm biến áp.
Scoring
| Subtask | Số điểm | Giới hạn |
|---|---|---|
| 1 | ~40~ | ~N \le 5000~ |
| 2 | ~60~ | Không có điều kiện gì thêm |
Sample Input 1
5
1 2
2 3
3 4
4 5
Sample Output 1
0.500000000
Sample Input 2
8
4 8
2 7
1 6
3 5
8 3
2 5
4 6
Sample Output 2
0.535714286
Notes
Sample 1:
Có ~C^2_5 = 10~ cách chọn 2 khu dân cư.
Có ~5~ cặp khu dân cư phù hợp là: 1-3, 2-4, 3-5, 1-4, 2-5.
Vậy xác suất chọn ra 2 khu dân cư phù hợp là ~5 / 10 = 0.5.~
Điểm: 100
Demenland bao gồm ~N~ thành phố được kết nối bởi ~N - 1~ con đường. Cũng có ~K~ cửa hàng, cửa hàng thứ ~i~ nằm ở thành phố ~a_i~. Vị trí của tất cả các cửa hàng đều khác biệt. Demen biết rằng khách hàng ~i~ sống ở thành phố ~i~. Khách hàng ~i~ có cửa hàng yêu thích nằm ở thành phố ~f_i~ và họ có giá trị kiên nhẫn là ~p_i~.
Ta quy ước rằng khoảng cách giữa 2 thành phố ~x~ và ~y~ là số con đường ít nhất cần phải đi qua để từ ~x~ đến ~y~ hoặc ngược lại. Với khách hàng thứ ~i~, giả sử khoảng cách từ thành phố ~i~ đến với cửa hàng gần nhất là ~d~. Nếu khoảng cách từ ~i~ đến ~f_i~ không vượt quá ~d + p_i~, khách hàng ~i~ sẽ ưu tiên đi đến thành phố ~f_i~. Ngược lại, họ sẽ đi đến cửa hàng gần nhất. Nếu có nhiều cửa hàng như thế, họ sẽ chọn một cửa hàng bất kỳ.
Bây giờ, Demen dự định sẽ khởi nghiệp với một cửa hàng, anh ấy cần chọn vị trí để xây cửa hàng đó. May mắn thay, Demen khá nổi tiếng nên nếu cửa hàng của anh ấy cùng gần nhất với nhiều cửa hàng khác tính từ thành phố ~i~, khách hàng ~i~ chắc chắn sẽ đi cửa hàng của Demen nếu không đi được cửa hàng yêu thích của họ. Demen đang cần tính xem nếu anh ấy xây dựng cửa hàng tại thành phố ~x~, sẽ có bao nhiêu khách hàng đến cửa hàng của anh ấy?
Input
Dòng đầu tiên bao gồm 2 số nguyên dương ~N~ và ~K~ (~1 \leq K \leq N \leq 3 \cdot 10^5~).
~N - 1~ dòng tiếp, dòng thứ ~i~ chứa ~2~ số nguyên dương ~x_i~ và ~y_i~ mô tả có con đường nối giữa 2 thành phố này.
Dòng tiếp theo chứa ~K~ số nguyên dương ~a_i~ (~1 \leq a_i \leq N~) chính là vị trí của ~K~ cửa hàng.
N dòng tiếp theo, dòng thứ ~i~ chứa ~2~ số nguyên dương ~f_i~ và ~p_i~ (~1 \leq f_i \leq N, 0 \leq p_i \leq N - 1~) lần lượt là cửa hàng yêu thích và giá trị kiên nhẫn của khách hàng ~i~.
Output
In ra ~N~ số nguyên dương, số thứ ~i~ chính là số khách hàng sẽ đến cửa hàng của Demen nếu anh ấy đặt cửa hàng tại thành phố ~i~.
Sample Input 1
4 1
1 2
1 3
2 4
1
1 1
1 0
1 1
1 0
Sample Output 1
0 2 0 1
Sample Input 2
6 3
1 2
2 3
3 4
4 5
5 6
1 2 6
6 3
6 1
6 2
1 4
2 0
1 1
Sample Output 2
1 1 1 1 1 2