Bedao Regular Contest 19
Điểm: 100
Cho hai số nguyên dương ~x,k~.
Tìm số nguyên dương ~y~ bé nhất sao cho ~x \times y~ chia hết cho ~k~.
Input
Gồm một dòng duy nhất chứa hai số nguyên ~x,k~ cách nhau bởi dấu cách (~x,k \le 10^{18}~).
Output
Gồm một số nguyên dương duy nhất là đáp án của đề bài.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~50~ | ~x, k \leq 10^6~ |
| 2 | ~50~ | ~x, k \leq 10^{18}~ |
Sample Input 1
8 6
Sample Output 1
3
Sample Input 2
12 7
Sample Output 2
7
Điểm: 100
Cho dãy ~a_1, a_2, ..., a_n~ nguyên không âm.
Bạn hãy tìm dãy số ~s_1, s_2, \ldots, s_k~ dài nhất thỏa mãn:
~1 \le s_1 < s_2 < \ldots < s_k \le n~.
Phép AND của mọi giá trị tương ứng trong tập có giá trị khác ~0~.
Yêu cầu: Hãy cho biết số lượng lớn nhất các phần tử có thể của tập ~A~.
Input
Dòng đầu tiên chứa số nguyên dương ~n~ ~(n \le 10^6)~ là số phần tử của dãy ~a~.
Dòng tiếp theo chứa ~n~ số nguyên không âm ~a_1, a_2, ..., a_n~ ~(0 \le a_i \le 10^9)~.
Output
Đưa ra một số nguyên ~K~ là số phần tử lớn nhất có thể của tập ~S~.
Sample Input 1
5
1 2 3 4 5
Sample Output 1
3
Điểm: 100
Cho dãy số gồm ~n~ số nguyên dương ~a_1, a_2, \ldots, a_n~.
Bạn hãy tìm dãy số ~b_1, b_2, \ldots, b_k~ dài nhất thỏa mãn:
~1 \le b_1 < b_2 < \ldots < b_k \le n~.
~a_{b_1} + 1 = a_{b_2} + 2 = \ldots = a_{b_k} + k~.
Input
Dòng đầu tiên gồm một số nguyên dương ~n~ là số lượng phần tử của dãy ~a~ (~1 \le n \le 10^6~).
Dòng thứ hai chứa ~n~ số nguyên dương mô tả dãy ~a_1, a_2, \ldots a_n~. (~1 \le a_i \le 10^6~, ~1 \le i \le n~).
Output
Dòng thứ nhất in ra một số nguyên dương ~k~ là số lượng phần tử của dãy ~b~ dài nhất tìm được.
Dòng thứ hai in ra ~k~ số nguyên dương mô tả dãy ~b_1, b_2, \ldots, b_k~.
Nếu có nhiều dãy ~b~ thỏa mãn thì in ra một dãy bất kì.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~30~ | ~n \le 20~ |
| 2 | ~40~ | ~n \le 5000~ |
| 3 | ~20~ | ~n \le 10^5~ |
| 4 | ~10~ | Không có ràng buộc gì thêm |
Sample Input 1
7
5 6 1 4 2 3 2
Sample Output 1
4
1 4 6 7
Điểm: 100
Gọi ~S(l,r,a)~ là Set của các phần tử từ ~l~ tới ~r~ trong mảng ~a~. Ví dụ, nếu ~a = [1,1,1,3,3,2]~ thì ~S(1,6, a) = [1,2,3]~; ~S(4,6,a) = [2,3]~.
Cho hai mảng các số nguyên dương ~a~ và ~b~ có kích thước là ~n~. Bạn có ~q~ truy vấn, truy vấn thứ ~i~ cho bốn số ~l_i~, ~r_i~ và ~x_i~, ~y_i~. Với mỗi truy vấn, hãy kiểm tra xem ~S(l_i,r_i,a)~ có bằng với ~S(x_i,y_i,b)~ hay không.
Input
Dòng đầu tiên chứa hai số nguyên dương ~n~ và ~q~ (~1 \leq n, q \leq 2 \cdot 10^5~).
Dòng tiếp theo chứa ~n~ số nguyên dương là các phần tử mảng ~a~ (~1 \leq a_i \leq 10^9~).
Dòng tiếp theo chứa ~n~ số nguyên dương là các phần tử mảng ~b~ (~1 \leq b_i \leq 10^9~).
~q~ dòng tiếp, dòng thứ ~i~ chứa ~4~ số nguyên dương ~l_i~, ~r_i~ và ~x_i~, ~y_i~ (~1 \leq l_i \leq r_i \leq n~, ~1 \leq x_i \leq y_i \leq n~).
Output
- In ra ~q~ dòng, nếu ~S(l_i,r_i,a)~ bằng với ~S(x_i,y_i,b)~ in ra ~\textbf{YES}~, ngược lại in ra ~\textbf{NO}~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~20~ | ~n,q \le 5000~ |
| 2 | ~20~ | ~n,q \le 2 \times 10^5~ và ~a_i, b_i \le 100~ |
| 3 | ~30~ | ~n,q \le 2 \times 10^5~ và ~l_i = 1, x_i = 1~ |
| 4 | ~30~ | Không có ràng buộc gì thêm |
Sample Input 1
6 5
1 1 1 2 3 2
1 2 1 3 2 1
1 6 1 6
3 6 2 5
2 5 4 5
1 4 2 3
1 3 2 4
Sample Output 1
YES
YES
NO
YES
NO
Điểm: 100
Bạn đang leo dốc trong một thành phố trên núi.
Nơi thành phố bạn sống đặc biệt có những con đường cao tít tựa Đà Lạt. ~N~ căn nhà nơi đây có thể đến được với nhau bằng ~M~ con đường hai chiều, con đường thứ ~i~ có độ dài ~w_i~ và độ cao là ~c_i~. Căn nhà cuối cùng (thứ ~N~) trên đỉnh núi là nơi bạn cần đến, từ căn nhà số ~1~ bạn cần đến đó nhanh nhất có thể nhưng điều đó không thành vấn đề vì bạn đã quá rành đường nơi đây rồi.
Điều bạn cần là tìm con đường có thể tối đa hoá độ cao giữa đường cao nhất và đường thấp nhất mà vẫn đảm bảo về thời gian, bởi leo trèo là việc bạn thích nhất. Liệu bạn có biết chênh lệch tối đa đó không?
Input
Dòng đầu tiên gồm hai số nguyên dương là ~N~ và ~M~ (~1 \leq N \leq 2 \cdot 10^5, 1 \le M \leq 3 \cdot 10^5~).
~M~ dòng tiếp theo dòng thứ ~i~ gồm bốn số ~u_i~, ~v_i~, ~w_i~, ~c_i~ (~1 \leq u_i \neq v_i \leq N~, ~1 \leq w_i, c_i \leq 10^9~) lần lượt cho biết độ dài và độ cao của con đường nối hai địa điểm ~u_i~ và ~v_i~. Giữa hai địa điểm không có quá một con đường.
Đề đảm bảo luộn tồn tại đường đi từ ~1~ đến ~N~.
Output
Ghi ra một số duy nhất cho biết chênh lệch lớn nhất bạn cần mà vẫn đảm bảo thời gian di chuyển là ngắn nhất.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~30~ | ~N \leq 50~, ~M \leq 200~, ~c_i \leq 20~ |
| 2 | ~30~ | ~N \leq 10^4~, ~c_i \leq 50~ |
| 3 | ~40~ | Không có ràng buộc gì thêm |
Sample Input 1
6 8
4 6 1 8
1 3 1 10
3 4 1 6
2 6 1 1
5 2 1 5
3 5 1 4
1 5 1 2
4 5 1 7
Sample Output 1
6
Điểm: 100
Quân đội của đại tướng Trần có ~n~ đơn vị được đánh số từ ~1~ đến ~n~. Đơn vị ~1~ có cấp bậc cao nhất, còn các đơn vị ~i~ với ~2 \le i \le n~ sẽ nhận đơn vị ~p_i~ làm cấp trên trực tiếp. Đảm bảo rằng, cách sắp xếp cấp bậc này được dựa trên mô hình cây. Nói cách khác, mô hình quân đội là một cây có gốc ở đỉnh ~1~. Ngoài ra, đơn vị thứ ~i~ có quân số là ~a_i~.
Một cách triệu tập quân đội với đơn vị ~u~ là chỉ huy là việc chọn một dãy các đơn vị ~x_1, x_2, \dots, x_k~, mỗi đơn vị lấy duy nhất một binh sĩ, sao cho ~x_1 = u~ và ~p_{x_{i+1}} = x_i~ với ~1 \le i \le k - 1~.
Gọi ~S(u)~ là số cách triệu tập quân đội với ~u~ là chỉ huy.
Để kiểm tra sự linh hoạt của hệ thống quân đội, đại tướng Trần cần bạn thiết kế một chương trình thực hiện một dãy các thao tác sau:
Thay đổi quân số của một đơn vị bất kỳ.
Chọn một đơn vị ~u~ bất kỳ, tính ~S(u)~.
Yêu cầu: Hãy thực hiện các yêu cầu trên của đại tướng để nhận được phần thưởng hậu hĩnh.
Input
Dòng đầu tiên gồm hai số nguyên ~n~ và ~q~ (~1 \le n, q \le 2 \cdot 10^5~) — số đơn vị và số yêu cầu của đại tướng Trần.
Dòng thứ hai gồm ~n - 1~ số nguyên dương ~p_2, p_3, \dots, p_n~ (~p_i \lt i~) — cấp trên trực tiếp của đơn vị ~i~.
Dòng thứ ba gồm ~n~ số nguyên dương ~a_1, a_2, \dots, a_n~ (~1 \le a_i \le 10^9~) — quân số của đơn vị ~i~.
~q~ dòng cuối cùng, mỗi dòng là một truy vấn thuộc một trong hai dạng:
~1~ ~u~ ~x~ (~1 \le u \le n, 1 \le x \le 10^9~): Gán ~a_u = x~.
~2~ ~u~ (~1 \le u \le n~): Tính ~S(u)~.
Output
- Với mỗi truy vấn loại ~2~, in ra một số nguyên trên một dòng là kết quả của truy vấn, lấy dư cho ~10^9 + 7~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~30\%~ | Không có truy vấn loại 1. |
| 2 | ~30\%~ | ~p_{i+1} = i, \forall i: 1 \le i \le n - 1~. |
| 3 | ~40\%~ | Không có ràng buộc gì thêm. |
Sample Input 1
4 3
1 2 2
1 1 2 2
2 2
1 2 2
2 2
Sample Output 1
5
10
Notes
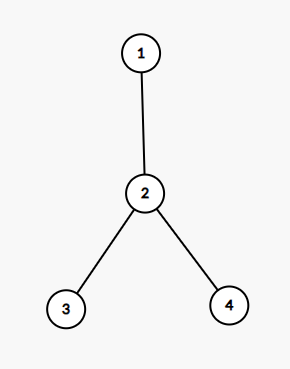
Minh họa ví dụ.
Ta có dãy ban đầu ~a = [1,1,2,2]~. Định nghĩa ~x_y~ là binh sĩ thứ ~y~ ở đơn vị ~x~.
Khi ~a_2 = 1~ thì ~S(2) = 5~, gồm các cách chọn sau: ~[2_1]~, ~[2_1,3_1]~, ~[2_1,3_2]~, ~[2_1,4_1]~, ~[2_1,4_2]~.
Sau khi cập nhật ~a_2 = 2~, ta có thêm ~5~ cách chọn nữa, mỗi cách đều chọn binh sĩ ~2_2~.