Bedao OI Contest 7 - Day 1
Điểm: 7
Bạn có hai tài khoản email, lần lượt có mật khẩu là ~S_1~ và ~S_2~.
Ô để nhập mật khẩu ở email 1 có độ dài là ~L_1~, tương tự với ô của email 2 có độ dài là ~L_2~.
Để nhập mật khẩu, bạn được điền 26 kí tự latin và kí tự '<' (tức là xóa một kí tự). Giả sử bạn đang điền mật khẩu cho email 1 ở ô độ dài là ~L_1~, gọi ~T~ là giá trị xâu đang điền, ~|T|~ là độ dài của xâu ~T~:
Nếu ~|T| = 0~: khi bạn điền '<' (tức là xóa), không có gì xảy ra. Ngược lại nếu ~|T| > 0~ thì bạn xóa đi kí tự cuối cùng.
Nếu ~|T| = L_1~, thì nếu bạn điền thêm kí tự, xâu ~T~ sẽ không thay đổi (do đã tràn ra khỏi số kí tự có thể lưu), ngược lại thì xâu ~T~ sẽ nhận giá trị vừa điền vào cuối.
Vì sợ máy tính của mình bị cài keylog, bạn quyết định sẽ tạo ra một cách điền mang tính bảo mật như sau:
Gọi ~S~ là xâu chứa thao tác cách điền của bạn. Nếu bạn thực hiện thao tác biểu diễn bởi ~S~ cho ô mật khẩu 1, thì kết quả thu được là ~S_1~. Ngược lại là ~S_2~.
Bạn muốn độ dài xâu ~S~ là nhỏ nhất có thể.
Yêu cầu: Hãy tìm xâu ~S~ tương ứng.
Input
Dữ liệu vào từ file văn bản password.inp.
Dòng đầu tiên gồm xâu ~S_1~ và số nguyên ~L_1~ ~(1 \le |S_1| \le L_1 \le 1000)~ — lần lượt là mật khẩu và độ dài của ô để nhập mật khẩu của email 1.
Dòng thứ hai gồm xâu ~S_2~ và số nguyên ~L_2~ ~(1 \le |S_2| \le L_2 \le 1000)~ — lần lượt là mật khẩu và độ dài của ô để nhập mật khẩu của email 2.
Xâu ~S_1~ và ~S_2~ chỉ chứa các chữ cái tiếng Anh in thường.
Lưu ý: ~|S|~ là độ dài của xâu ~S~.
Output
Ghi ra file văn bản password.out.
Dòng đầu tiên gồm độ dài của xâu ~S~ tương ứng. Nếu không tồn tại xâu ~S~ thỏa mãn, in ra ký tự "!".
Dòng thứ hai gồm xâu ~S~ tương ứng, nếu tồn tại.
Lưu ý: Thí sinh sẽ được ~50\%~ số điểm của một test nếu in ra đúng độ dài xâu ~S~, ~100\%~ số điểm nếu in ra được xâu ~S~ thỏa mãn yêu cầu.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | ~10\%~ | Mật khẩu chỉ gồm 2 ký tự "a" và "b"; ~L_1, L_2 \le 5~ |
| ~2~ | ~20\%~ | ~L_1, L_2 \le 50~ |
| ~3~ | ~30\%~ | ~L_1, L_2 \le 200~ |
| ~4~ | ~40\%~ | Không có ràng buộc gì thêm. |
Sample Input 1
ab 3
abc 4
Sample Output 1
5
abcq<
Sample Input 2
abb 3
abc 4
Sample Output 2
!
Notes
Ví dụ 1 :
Chuỗi ~S~ là cách điền thao tác nhỏ nhất để tạo ra ~S_1~. Khi thực hiện các thao tác :
'a' ~\to~ "a".
'b' ~\to~ "ab".
'c' ~\to~ "abc". (Đã đạt độ dài tối đa là ~L_1 = 3~).
'q' ~\to~ "abc". (Xâu kí tự không thay đổi vì đạt đến độ dài tối đa của ~L_1~).
'<' ~\to~ Xóa ký tự 'c', xâu hiện tại trở thành là "ab".
Sau khi thực hiện, ta được ~S_1 = \texttt{"ab"}~.
Tương tự, để tạo ra ~S_2~. Khi thực hiện các thao tác:
'a' ~\to~ "a".
'b' ~\to~ "ab".
'c' ~\to~ "abc"
'q' ~\to~ "abcq" (đã đạt độ dài tối đa là ~L_2 = 4~).
'<' ~\to~ Xóa ký tự 'q', xâu hiện tại là "abc".
Tương tự, ta được ~S_2 = \texttt{"abc"}.~
Điểm: 7
Hưng là một người thích những cơn mưa, nhưng mỗi khi ngắm mưa lại gợi cho cậu những kỷ niệm buồn. Để vơi đi nỗi buồn, Hưng đã mang các khối hình hộp chữ nhật ra chơi.
Hưng có ~N~ khối hình hộp chữ nhật có chiều rộng bằng nhau. Hưng sẽ sắp xếp lại những khối chữ nhật đó để thu thập lượng mưa lớn nhất. Để đạt được điều này, cậu sẽ đặt ~N~ khối trên một hàng, không được phép có khoảng trống giữa các khối. Cậu có thể xoay một số khối chữ nhật để đổi chiều dài và chiều cao hoặc giữ nguyên nhưng không được thay đổi chiều rộng.
Cách sắp xếp các khối hình chữ nhật sẽ tạo ra các "bể nước" và Hưng sẽ thu được nước mưa bằng đúng diện tích các bể. Vì đang còn những u sầu nên Hưng không thể nghĩ ra cách xếp tối ưu. Bạn hãy giúp cậu tìm cách sắp xếp các khối hình hộp chữ nhật sao cho lượng nước mưa thu được là nhiều nhất.
Input
Dòng đầu tiên là số nguyên dương ~N~ ~(3 \leq N \leq 3 \cdot 10 ^ 5)~ — số lượng khối hình hộp chữ nhật mà Hưng có.
~N~ dòng tiếp theo, dòng thứ ~i~ chứa hai số nguyên ~w_i~, ~h_i~ ~(1 \leq w_i, h_i \leq 10 ^ 6)~ — chiều dài và chiều cao của hình chữ nhật thứ ~i~.
Output
In ra một số nguyên dương duy nhất, biểu thị diện tích nước tối đa mà Hưng có thể thu được nếu anh ta sắp xếp các khối hình hộp chữ nhật một cách tối ưu.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~10~ | ~N = 3~ |
| 2 | ~20~ | ~w_i = h_i~ |
| 3 | ~20~ | ~N \leq 100~ |
| 4 | ~20~ | ~N \leq 2500~ |
| 5 | ~30~ | Không có ràng buộc gì thêm |
Sample Input 1
3
4 3
2 6
5 1
Sample Output 1
15
Sample Input 2
3
1 2
2 1
1 1
Sample Output 2
1
Notes
Ở ví dụ 1: Đặt các hình chữ nhật kề nhau theo cặp (chiều dài, chiều cao) như sau: (3, 4) (5, 1) (2, 6).
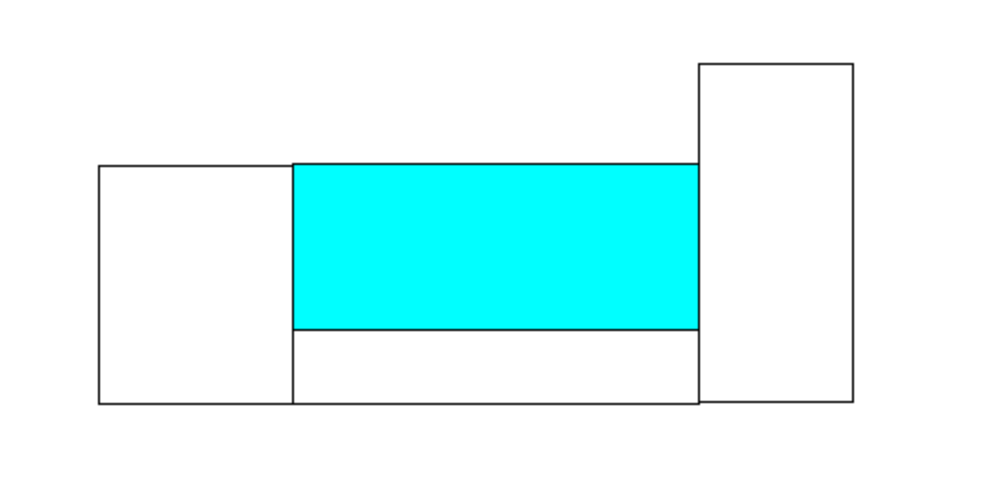
Ở ví dụ 2: Đặt các hình chữ nhật kề nhau theo cặp (chiều dài, chiều cao) như sau: (1, 2) (1, 1) (1, 2).
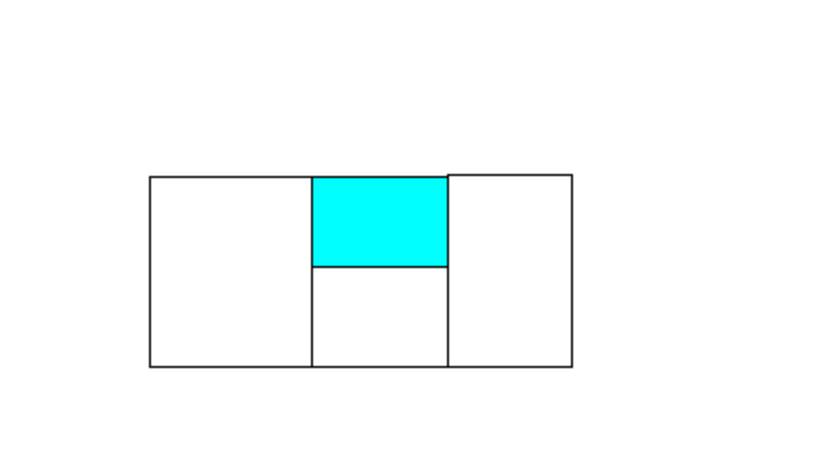
Điểm: 6
Quân có một đồ thị hai chiều liên thông gồm ~n~ đỉnh và ~m~ cạnh, cạnh thứ ~i~ nối giữa đỉnh ~u_i~ với ~v_i~ và có trọng số là ~w_i~. Bảo thực hiện thao tác sau chính xác một lần lên đồ thị của Quân:
Chọn cạnh thứ ~i~ và cạnh thứ ~j~ (~i < j~) và gán ~w_i~ = ~w_i~ + ~w_j~.
Bảo muốn tối đa hoá đường đi ngắn nhất từ đỉnh ~1~ tới đỉnh ~n~ trên đồ thị mới này. Hãy giúp Bảo tính xem độ dài đường đi ngắn nhất từ đỉnh ~1~ tới đỉnh ~n~ lớn nhất có thể là bao nhiêu.
Input
Dòng đầu tiên chứa số nguyên dương ~n~ và ~m~ ~(1 \le n,m \le 3 \cdot 10^5).~
~m~ dòng tiếp theo, dòng thứ ~i~ chứa ba số nguyên ~u_i~, ~v_i~, ~w_i~ biểu thị cạnh nối thứ ~i~ ~(1 \le u_i, v_i \le n, 0 \le w_i \le 10^9).~
Output
In ra một số là kết quả của bài toán.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~10~ | ~n,m\le100~ |
| 2 | ~10~ | ~n,m \le 2000~ |
| 3 | ~10~ | ~m=n-1~ |
| 4 | ~20~ | ~w_i=1~ ~\forall~ i ~\in~ [1,~m~] |
| 5 | ~25~ | ~w_i \le 10~ ~\forall~ i ~\in~ [1,~m~] |
| 1 | ~25~ | Không có ràng buộc gì thêm |
Sample Input 1
6 8
1 2 2
1 3 4
2 3 1
3 5 3
2 5 3
2 6 3
5 6 2
6 4 1
Sample Output 1
8
Notes
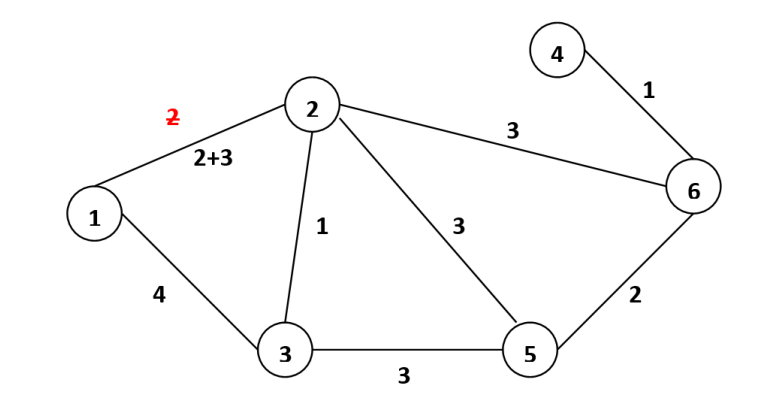
Bảo chọn cạnh ~(1, 2)~ và ~(2, 6)~ và gán trọng số cạnh ~(1, 2)~ thành ~2 + 3 = 5~.
Đường đi ngắn nhất: ~1 - 2 - 6~