Bedao Grand Contest 17
Điểm: 100
Cho ~n~ điểm ~(x, y)~ nằm trên hệ trục tọa độ, điểm thứ ~i~ có trọng số là ~w_i~.
Cho ~q~ truy vấn, mỗi truy vấn có dạng một số nguyên dương ~r~:
Cho một đường tròn tâm ~(0, 0)~ bán kính ~r~.
Tính tổng trọng số của các điểm nằm trong đường tròn (tính cả các điểm nằm trên đường tròn).
Input
Dòng đầu tiên là 2 số nguyên (~1 \leq n, q \leq 5 \times 10^5~).
Dòng thứ ~i~ trong số ~n~ dòng tiếp theo, mỗi dòng chứa ba số nguyên ~x, y, w~ cách nhau bởi dấu cách, biểu diễn thông tin của một điểm trên trục tọa độ (~|x|, |y|, |w| \leq 10^9~).
Trong ~q~ dòng tiếp theo, dòng thứ ~j~ (~1 \leq j \leq q~) chứa một số nguyên ~r_j~ (~1 \leq r_j \leq 10^9~) biểu diễn một đường tròn tâm ~(0, 0)~ bán kính ~r_j~.
Output
In ra ~q~ dòng, dòng thứ ~j~ là đáp án cho truy vấn thứ ~j~: tổng trọng số của các điểm nằm trong đường tròn tâm ~(0, 0)~ bán kính ~r_j~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~20~ | ~n, q \le 2000~ |
| 2 | ~30~ | ~w = 1~ |
| 3 | ~50~ | Không có ràng buộc gì thêm |
Sample Input 1
6 3
-2 -2 1
1 1 2
-1 2 3
2 0 4
0 3 5
1 -3 6
3
2
1
Sample Output 1
15
6
0
Notes
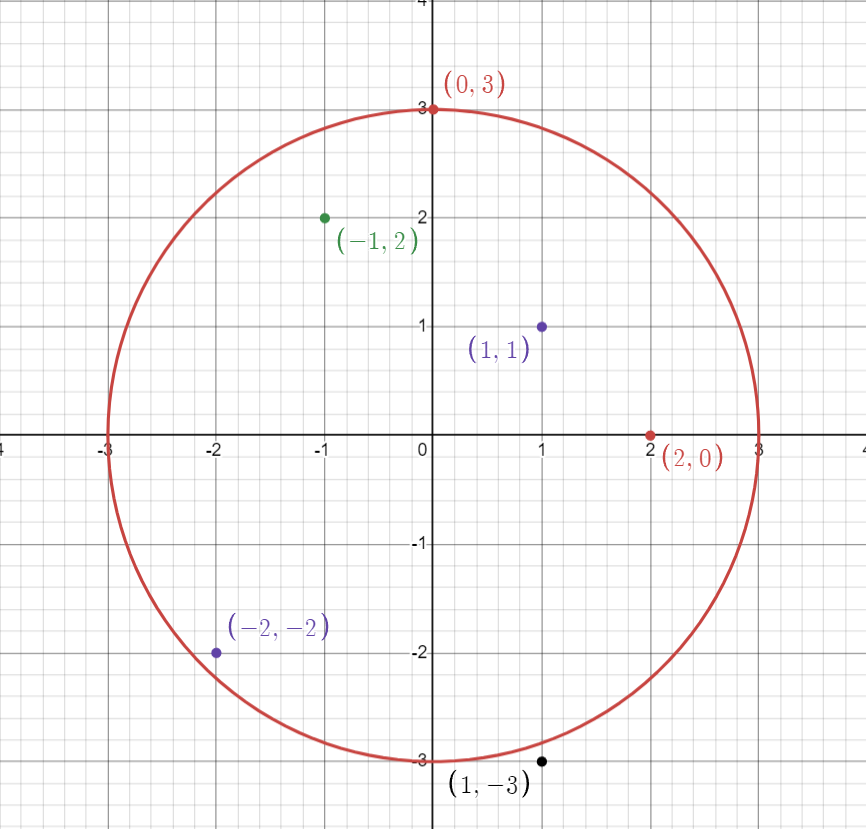
Trong truy vấn ~r=3~, có ~4~ điểm nằm hoàn toàn bên trong đường tròn và ~1~ điểm nằm trên đường tròn ~\Rightarrow~ Đáp án là ~1 + 2 + 3 + 4 + 5 = 15~.
Trong truy vấn ~r=2~, có ~2~ điểm ~(1, 1)~ và ~(2, 0)~ nằm trong đường tròn.
Trong truy vấn ~r=1~, không có điểm nào nằm trong đường tròn.
Điểm: 100
Một cấu trúc bông tuyết ~x~ cánh được xây dựng như sau:
Ban đầu chỉ có một nút.
Ở mỗi bước, các nút có ít hơn hai cạnh nối với các nút khác sẽ được nối thêm ~x~ nút mới.
Cho ~t~ truy vấn, mỗi truy vấn cho một số ~n~. Xác định xem có tồn tại cặp số ~x~ và ~i~ nào sao cho sau ~i~ (~x, i > 1~) bước thì bông tuyết có đúng ~n~ nút không. Nếu có in ra ~x~ và ~i~, ngược lại in ~-1~. Nếu có nhiều đáp án, hãy in ra đáp án có ~x~ bé nhất.
Input
Dòng đầu tiên gồm một số nguyên dương ~t~ (~1 \le t \le 5 \cdot 10^5~) — số lượng truy vấn của bài toán.
~t~ dòng tiếp theo, mỗi dòng là một số nguyên dương ~n~ (~1 \le n\le 10^{18}~).
Output
Gồm ~t~ dòng là kết quả của truy vấn thứ ~i~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~20~ | ~t \le 10^3, n \le 10^{12}~ |
| 2 | ~30~ | ~t \le 5 \cdot 10^5, n \le 10^{12}~ |
| 3 | ~50~ | Không có ràng buộc gì thêm |
Sample Input 1
6
1
2
7
13
14
15
Sample Output 1
-1
-1
2 2
3 2
-1
2 3
Sample Input 2
2
68719476735
15690529804
Sample Output 2
2 35
3 21
Điểm: 100
Được vào TP.HCM lần đầu trong đời, Shine khám phá ra được Maimai và muốn chơi hết các Cab Maimai ở TP.HCM.
TP.HCM được biểu diễn trên mặt phẳng ~Oxy~, trong đó có ~n~ Cab Maimai được hiểu như là ~n~ điểm trên mặt phẳng ~Oxy~.
Dành dụm tiền đi dạy bấy lâu nay của mình, Shine có thể mua được ~3~ lô đất hình vuông bằng nhau có độ dài cạnh là một số nguyên dương ~d > 0~. Các lô đất có thể chồng lên nhau, một Cab Maimai cậu có thể chơi được nếu nó nằm trong ~1~ trong ~3~ lô đất mà cậu mua (có thể nằm trên viền của lô đất).
Vì kinh tế thời buổi này khó khăn, nên Shine muốn diện tích lô đất của mình là nhỏ nhất có thể, bạn hãy giúp cậu ấy tìm diện tích nhỏ nhất có thể của các lô đất cậu ấy mua.
Input
Dòng đầu tiên gồm ~1~ số nguyên dương ~n~ (~1 \le n \le 10^{5}~) — Số lượng Cab Maimai trong TP.HCM
Trong ~n~ dòng tiếp theo, dòng thứ ~i~ gồm ~2~ số nguyên ~x_i~, ~y_i~ (~-10^{9} \le x_i, y_i \le 10^{9}~) — Miêu tả vị trí của ~n~ Cab Maimai.
Output
Một số duy nhất là diện tích nhỏ nhất của các hình vuông, sao cho Shine có thể chơi hết các Cab Maimai ở TP.HCM.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~20~ | ~n = 4~ |
| 2 | ~30~ | ~4 \lt n \le 15~ |
| 3 | ~50~ | Không có ràng buộc gì thêm |
Sample Input 1
4
2 2
4 1
3 4
7 3
Sample Output 1
4
Sample Input 2
6
3 2
6 2
3 4
7 3
3 3
3 1
Sample Output 2
1
Notes
Trong ví dụ thứ 2, Shine sẽ mua ~3~ lô đất hình vuông có độ dài cạnh là ~1~:
Lô đất thứ nhất bao phủ ~2~ Cab Maimai ở vị trí (~3, 1~) và (~3, 2~).
Lô đất thứ hai bao phủ ~2~ Cab Maimai ở vị trí (~3, 3~) và (~3, 4~).
Lô đất thứ ba bao phủ ~2~ Cab Maimai ở vị trí (~6, 2~) và (~7, 3~).
Và thế là Shine có thể chơi hết được ~6~ Cab Maimai.
Điểm: 100
Nếu đã học qua đại số, ta sẽ không lạ lẫm gì về việc khai triển công thức ~(x + 1)^n~.
~(x + 1)^1 = x + 1~
~(x + 1)^2 = x^2 + 2x + 1~
~(x + 1)^3 = x^3 + 3x^2 + 3x + 1~
~(x + 1)^4 = x^4 + 4x^3 + 6x^2 + 4x + 1~
~\ldots~
Và hệ số của ~x^k~ trong khai triển ~(x + 1)^n~ đúng bằng ~C_{n}^{k}~.
Ta quy định, ~F(n)~ là tổng số lượng số ~k~ ~(0 \le k \le n)~ có hệ số ~x^k~ cùng đồng dư với ~\phi~ khi ~\mod 2~. Hay nói cách khác: ~F(n) = \sum_{k = 0}^{n} [C_{n}^{k} \equiv \phi \mod 2]~ — với ~\phi~ là một số cho trước.
Có ~q~ truy vấn cần giải quyết. Ở truy vấn thứ ~t~, ta được cho ~2~ số nguyên ~l_t, r_t~ ta cần xác định ~S_t = \left(\sum_{i = l_t}^{r_t} F(i) \right) \bmod (10^9+7)~.
Input
Dòng đầu tiên gồm ~2~ số nguyên ~q, \phi~ (~1 \le q \le 10^5, 0 \le \phi \le 1~) – thể hiện số lượng truy vấn và giá trị của ~\phi~.
~q~ dòng tiếp theo, mỗi dòng gồm ~2~ số nguyên ~l_t, r_t~ (~1 \le l_t \le r_t \le 10^{18}~).
Output
- In ra ~q~ dòng, dòng thứ ~t~ là giá trị ~S_t~ tính được (~1 \le t \le q~).
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~10~ | ~\max_{t = 1}^{q} r_t \le 10^3~ |
| 2 | ~20~ | ~\max_{t = 1}^{q} r_t \le 10^5~ |
| 3 | ~70~ | Không có ràng buộc gì thêm |
Sample Input 1
2 0
1 4
3 4
Sample Output 1
4
3
Sample Input 2
2 1
1 2
3 4
Sample Output 2
4
6
Notes
Bên dưới là Tam giác Pascal:
| ~C_k^n~ | k | |||||
|---|---|---|---|---|---|---|
| 3-7 | 0 | 1 | 2 | 3 | 4 | |
| n | 0 | 1 | ||||
| 1 | 1 | 1 | ||||
| 2 | 1 | 2 | 1 | |||
| 3 | 1 | 3 | 3 | 1 | ||
| 4 | 1 | 4 | 6 | 4 | 1 | |
| 1-2 |
Trong ví dụ 1, các cặp ~\{n,k\}~ thoả mãn là:
Truy vấn 1: ~\{2,1\}~, ~\{4,1\}~, ~\{4,2\}~, ~\{4,3\}~
Truy vấn 2: ~\{4,1\}~, ~\{4,2\}~, ~\{4,3\}~
Trong ví dụ 2, các cặp ~\{n,k\}~ thoả mãn là:
Truy vấn 1: ~\{1,0\}~, ~\{1,1\}~, ~\{2,0\}~, ~\{2,2\}~
Truy vấn 2: ~\{3,0\}~, ~\{3,1\}~, ~\{3,2\}~, ~\{3,3\}~, ~\{4,0\}~, ~\{4,4\}~.
Điểm: 100
Thành phố H vừa mới mở tuyến đường sắt đô thị (Metro) đầu tiên. Sau ~10^9+7~ năm thi công, người dân rất mong chờ được trải nghiệm loại hình giao thông mới mẻ này.
Là trưởng ban tài chính của công ty Metro mới thành lập, bạn cần đặt giá vé tháng sao cho doanh thu thu về là cao nhất. Thành phố H có ~N~ người, người thứ ~i~ có thu nhập hàng tháng là ~a_i~ vàng và ~b_i~ ngọc (~a_i \ge b_i~).
Bạn cần đặt giá vé tháng là ~x~ vàng / ~y~ ngọc, sao cho ~x \ge y~. Khi đó mỗi người dân sẽ quyết định mua hay không mua vé tháng như sau:
Nếu ~a_i \ge x~, người thứ ~i~ sẽ mua vé tháng với giá ~x~ vàng.
Nếu ~a_i < x~ và ~b_i \ge y~, người thứ ~i~ sẽ mua vé tháng với giá ~y~ ngọc.
Nếu ~a_i < x~ và ~b_i < y~, người thứ ~i~ sẽ không mua vé tháng.
Hãy tìm cách đặt giá vé tháng sao cho doanh thu (bằng tổng số vàng và số ngọc) hàng tháng thu về là cao nhất.
Input
Dòng đầu tiên gồm 1 số nguyên ~N~ (~1 \le N \le 150000~): số người dân ở thành phố H.
~N~ dòng tiếp theo, mỗi dòng gồm 2 số nguyên ~a_i~ và ~b_i~ (~0 \le b_i \le a_i \le 10^9~) là thu nhập hàng tháng của người thứ i.
Output
In ra 1 số nguyên là doanh thu (bằng tổng số vàng và số ngọc) hàng tháng cao nhất có thể thu về.
Scoring
Subtasks
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~12~ | ~N, A_i, B_i \leq 100~ |
| 2 | ~14~ | ~N \leq 300~ |
| 2 | ~19~ | ~N \leq 3000~ |
| 2 | ~14~ | ~B_i = 0~ |
| 2 | ~19~ | ~A_i = B_i~ |
| 2 | ~11~ | ~N \leq 50000~ |
| 7 | ~11~ | Không có điều kiện gì thêm |
Sample Input 1
5
80 20
60 50
40 40
15 10
70 30
Sample Output 1
220
Sample Input 2
1
50 0
Sample Output 2
50
Điểm: 100
Bạn được cho một mảng ~a~ độ dài ~n~, bao gồm những số nguyên phân biệt. Mỗi phần tử trong mảng là một số nguyên dương không quá ~10^9~. Bạn cần tìm giá trị của tất cả các phần tử trong mảng.
Để làm vậy, bạn có thể thực hiện truy vấn thuộc hai loại sau:
"~1~ ~i~" ~(1 \leq i \leq n)~ — hỏi giá trị của ~a_i~
"~2~ ~k~ ~i_1, i_2, \ldots, i_k~" ~(2 \leq k \leq n, 1 \leq i_j \leq n,~ các giá trị ~i_j~ phân biệt~)~ — số ~k~ và ~k~ vị trí trong mảng. Sau khi hỏi truy vấn loại này bạn sẽ nhận được ~\frac{k(k - 1)}{2}~ số nguyên — ~|a_{i_c} - a_{i_d}|~ với mọi ~c < d~. Nói cách khác, bạn sẽ nhận được ~\frac{k(k - 1)}{2}~ giá trị tuyệt đối giữa các cặp phần tử trên các vị trí ~i_1, i_2, \ldots, i_k~. Lưu ý rằng đáp án cho truy vấn loại ~2~ được sắp xếp ngẫu nhiên.
Lưu ý: Trong bài này, số thao tác loại ~1~ bạn thực hiện không được vượt quá ~10~.
Khi bạn đã biết đáp án thì có thể in ra kết quả với truy vấn sau:
- "~3~ ~a_1, a_2, \ldots, a_n~" ~(1 \leq a_i \leq 10^9)~ — các phần tử trong mảng ~a~. Sau truy vấn này, chương trình của bạn phải kết thúc.
Interaction
Ban đầu, bạn cần nhập vào số nguyên ~n~ ~(1 \leq n \leq 250)~ — số phần tử của mảng.
Để thực hiện truy vấn loại ~1~, in ra "~1~ ~i~" ~(1 \leq i \leq n)~ và đọc vào một số nguyên — giá trị của ~a_i~.
Để thực hiện truy vấn loại ~2~, in ra "~2~ ~k~" ~(2 \leq k \leq n)~. Trên cùng dòng đó in ra ~k~ số nguyên phân biệt cách nhau bởi dấu cách — ~i_1, i_2, \ldots, i_k~ ~(1 \leq i_j \leq n)~. Sau truy vấn này đọc vào ~\frac{k(k - 1)}{2}~ số nguyên — ~|a_{i_c} - a_{i_d}|~ với mọi ~c < d~. Các giá trị này được cho theo thứ tự ngẫu nhiên.
Khi đã biết kết quả, in ra "~3~". Trên cùng dòng đó, in ra ~n~ số nguyên cách nhau bởi dấu cách — ~a_1, a_2, \ldots, a_n~ ~(1 \leq a_i \leq 10^9)~. Chương trình của bạn phải kết thúc sau truy vấn này.
Nếu bạn nhận được kết quả là ~-1~ khi hỏi một trong hai loại truy vấn đầu tiên thì bạn đã thực hiện nhiều lượt truy vấn hơn cho phép hoặc thực hiện một truy vấn không hợp lệ. Chương trình của bạn phải kết thúc ngay và sẽ nhận được kết quả ~\text{Wrong Answer}~. Nếu không kết thúc thì chương trình của bạn có thể nhận được các kết quả khác.
Scoring
Gọi ~Q~ là tổng số truy vấn loại ~1~ và ~2~ mà bạn thực hiện trong một test, phần trăm số điểm bạn nhận được ở test đó cho bởi:
| Giới hạn | Điểm |
|---|---|
| ~Q \leq 2 \times n~ | ~30\%~ |
| ~Q \leq 30~ | ~70\%~ |
| ~Q \leq 26~ | ~100\%~ |
Sample Input 1
2
100
200
Sample Output 1
1 1
1 2
3 100 200