Tạp chí VNOI - Số 1: Coding Challenge #3
đã đăng vào 15, Tháng 11, 2025, 23:42Coding Challenge
Coding Challenge là một chuyên mục thuộc Tạp chí VNOI, được xây dựng với mục tiêu mang đến cho cộng đồng lập trình thi đấu Việt Nam một sân chơi hữu ích và thiết thực nhằm giúp các độc giả củng cố kiến thức thuật toán và thúc đẩy tinh thần học hỏi, chia sẻ trong cộng đồng.
Hoạt động được tổ chức định kỳ hai lần mỗi tháng trên Fanpage VNOI, Group Facebook “Diễn đàn Tin học Việt Nam” và nền tảng chấm bài trực tuyến VNOJ. Toàn bộ các bài toán trong Coding Challenge được biên soạn bởi đội ngũ Tình nguyện viên thuộc Team Contest của VNOI. Chất lượng các bài toán Coding Challenge được đảm bảo về tính chuyên môn, có sự đa dạng về chủ đề và độ khó cũng như đáp ứng yêu cầu về tính chặt chẽ và chính xác.
Độc giả của Tạp chí VNOI có thể tham gia giải các bài toán thuộc Coding Challenge và gửi lời giải về cho Tạp chí. Những bài giải chất lượng sẽ được chọn lọc để đăng tải trong các số Tạp chí tiếp theo. Bên cạnh việc được ghi nhận và giới thiệu rộng rãi đến cộng đồng, các tác giả có lời giải được đăng tải sẽ nhận những phần quà tri ân từ VNOI nhằm khuyến khích tinh thần ham học hỏi và chia sẻ kiến thức đến cộng đồng
Các lời giải được chọn lọc để đăng công khai sẽ được đánh giá dựa trên tiêu chí về sự rõ ràng, mạch lạc, sáng tạo; có sự đầu tư trong diễn giải tư duy, cấu trúc và tính dễ hiểu. Đối với các bài toán có nhiều subtask, tác giả cần trình bày đầy đủ ý tưởng và hướng giải quyết cho tất cả các phần.
Phần thưởng dành cho mỗi lời giải được đăng tải trên Tạp chí là một bộ quà tặng gồm sổ tay, bút, sticker và móc khóa. Đặc biệt, với các tác giả có từ 03 bài giải trở lên được đăng trong chuyên mục, Ban biên tập Tạp chí sẽ gửi tặng một chiếc áo VNOI như lời tri ân cho những đóng góp tích cực đối với Coding Challenge.
Sau 03 số đầu tiên, Coding Challenge đã ghi nhận những kết quả rất ấn tượng. Đã có tổng cộng 2316 lượt nộp bài trên hệ thống và 26 lời giải chất lượng được gửi về cho Tạp chí. Đây là nguồn động lực to lớn để đội ngũ Tạp chí VNOI tiếp tục phát triển và mở rộng sân chơi học thuật này trong thời gian tới.
Coding Challenge #3
Coding Challenge #3 là một bài toán về đường đi ngắn nhất, với tập cạnh có trọng số. Bài toán này là phiên bản tổng quát hoá trên đồ thị của bài toán đổ xăng nổi tiếng mà ắt hẳn mọi người đều đã trải qua một lần. Điểm thú vị của dạng bài này chính là việc chúng ta sẽ cần tư duy để tạo ra một đồ thị mới nhằm có thể nắm đủ thông tin bài toán. Trong 3 Coding Challenge, đây chính là bài toán thử thách nhất.
Bài toán này ghi nhận 21 bài giải thành công với lời giải nhanh nhất chỉ tốn 43 phút kể từ lúc đề bài Coding Challenge #3 được công bố. Đội ngũ Tạp chí VNOI đã chọn ra 2 lời giải cho bài toán này đến từ các độc giả của Tạp chí.
Đề Bài
Đề bài gốc có thể được đọc trên hệ thống VNOJ
Coding Challenge #3 - Đổ Xăng
Đổ Xăng
Vương quốc VNOI gồm ~n~ thành phố được liên kết với nhau bằng ~m~ con đường hai chiều, đảm bảo rằng mọi cặp thành phố đều có đường đi trực tiếp hoặc gián tiếp tới nhau. Con đường thứ ~i~ kết nối hai thành phố ~u_i, v_i~, và sẽ tốn ~w_i~ lít xăng để đi qua.
Là một người đam mê du lịch, bạn lên kế hoạch cho chuyến đi chơi của mình tới VNOI. Bạn xuất phát từ thành phố ~st~ và có dự định đi tới thành phố ~en~ bằng xe của mình. Tất nhiên để đi xe thì phải tốn nhiên liệu, và xe của bạn có một bình chứa được tối đa ~t~ lít xăng.
VNOI có ~s~ trạm xăng. Trạm xăng thứ ~i~ được phân bố ở thành phố ~p_i~ và có chi phí cho mỗi lít xăng là ~c_i~. Ở mỗi trạm xăng, bạn có thể mua không giới hạn số xăng (tất nhiên xe bạn chỉ mang tối đa được ~t~ lít xăng thôi).
Bạn bắt đầu từ thành phố ~st~ và xe bạn ban đầu không có xăng - may mắn rằng đảm bảo luôn có trạm xăng ở thành phố nơi bạn xuất phát. Hãy tính số tiền ít nhất cần bỏ ra để hoàn thành hành trình từ ~st~ tới ~en~.
Input
- Dòng đầu gồm 3 số nguyên ~n, m, s~ (~2 \le n \le 1000; 1 \le m \le 10^4; 1 \le s \le 100~)
- Dòng tiếp theo gồm một số nguyên dương ~t~ (~1 \le t \le 10^5~) mô tả sức chứa của bình xăng.
- ~m~ dòng tiếp theo, dòng thứ ~i~ gồm ba số nguyên dương ~u_i, v_i, w_i~ (~1 \le u_i, v_i \le n; 1 \le w_i \le t~) miêu tả con đường thứ ~i~.
- ~s~ dòng tiếp theo, dòng thứ ~i~ gồm hai số nguyên dương ~p_i, c_i~ (~1 \le p_i \le n; 1 \le c_i \le 100~) miêu tả trạm xăng thứ ~i~.
- Dòng cuối cùng gồm hai số nguyên dương ~st, en~ (~1 \le st, en \le n~) miêu tả vị trí bắt đầu và đích đến của bạn.
Output
- In ra số tiền ít nhất cần để đi chuyến đi.
Subtask
- Subtask ~1~ (~30~\%): ~n \le 100~; ~m \le 100~; ~t \le 500~
- Subtask ~2~ (~30~\%): ~t \le 500~
- Subtask ~3~ (~40~\%): Không giới hạn gì thêm.
Sample Input 1
3 3 2
200
1 3 80
1 2 50
2 3 50
1 70
2 40
1 3
Sample Output 1
5500
Sample Input 2
5 5 3
100
1 2 80
2 5 80
1 3 40
3 4 60
4 5 60
1 8
2 9
3 2
1 5
Sample Output 2
1340
Sample Input 3
4 3 3
10
1 2 2
2 3 6
3 4 3
1 4
2 7
3 9
2 4
Sample Output 3
61
Minh Họa Sample:
Sample 1:

Sample 2

Sample 3

Lời giải #1
Subtask 1: ~n, m \leq 100, t \leq 500~
Tags:
DP,Dijkstra,Auxiliary Graph
Ta gọi ~f_{i, j}~ là số tiền ít nhất cần trả để đi đến đỉnh ~i~ và còn lại ~j~ lít xăng.
Với mỗi đỉnh ~f_{i, j}~ đã được tính, ta có thể chuyển trạng thái như sau:
- Mua thêm lít xăng nếu như đỉnh i tồn tại cây xăng ~f_{i, next_j}~ ~(j < next_j <= t)~. ~f_{i, next_j} = f_{i, j} + (next_j - j) * minCost_i~ với ~minCost_i~ là chi phí nhỏ nhất để mua ~1~ lít xăng tại đỉnh ~i~.
- Chuyển đến đỉnh ~v~ kề ~i~ nếu như ~j >= w~. ~f_{v, j - w} = f_{u, j}~
Độ phức tạp: ~O((n \times t + (m + n \times t \times t)) \times log_2(n \times t))~
Subtask 2: ~t \leq 500~
Tags:
Dijkstra,Auxiliary Graph.
Vẫn từ ý tưởng cũ, để dễ xử lí, ta tạo đỉnh ảo cho mỗi ~f_{i, j}~. Ở subtask 1, ta thấy rằng việc chuyển trạng thái cho ~f_{i, next_j}~ là khá lớn. Vậy nên, thay vì phải duyệt hết những ~next_j~, ta chỉ cần chuyển đến trạng thái ~f_{i, j + 1}~. Lúc này, số lượng cạnh cần xét sẽ giảm đi đáng kể !
Độ phức tạp: ~O((n \times t + (m + n \times t)) \times log_2(n \times t))~
Subtask 3: Không có giới hạn gì thêm
Tags:
Dijkstra,Auxiliary Graph.
Ta thấy rằng thay vì xem xét tất cả những đỉnh trong đồ thị gốc, ta chỉ quan tâm đến những đỉnh đặc biệt, những đỉnh này là những đỉnh mà có thể ảnh hưởng đến hàm ~f~ của chúng ta. Đầu tiên, ta định nghĩa những đỉnh đặc biệt là những đỉnh hoặc là ~st~, hoặc là ~en~, hoặc là tồn tại ít nhất ~1~ cây xăng ở nó, và khi ta đến đỉnh đặc biệt, ta buộc phải mua lít xăng (nếu có cây xăng). Ta dễ dàng thấy được số lượng đỉnh đặc biệt là rất là ít, chỉ khoảng ~\leq 101~!. Vậy nên, Ta sẽ xem xét xem với cặp đỉnh ~(u, v)~ đặc biệt, chi phí thấp nhất để từ ~u \to v~ là bao nhiêu. Điều này ta có thể dễ dàng làm được bằng việc dijkstra trên đồ thị gốc. Ta gọi ~minCost_{u, v}~ là số lít nhỏ nhất để có thể đi từ ~u \to v~. Lúc này, hàm quy hoạch động của chúng ta giảm số lượng thái từ ~n \times t~ về ~s \times t~. Nhưng... vẫn còn quá lớn ?. Ta có một nhận xét quan trọng như sau: nếu khi đến đỉnh đặc biệt ~u~, vì ta buộc phải mua lít xăng ở ~u~, ta có thể giảm số trạng thái chiều ~j~ không phải là ~t~ mà là ~2 \times s~ (khoảng ~2 \times 10^4~, bé hơn ~t~ nhiều). Đầu tiên, ta quan sát rằng, khi tại đỉnh ~u~, ta chỉ nên mua đủ để đi đến ~v~ hoặc mua đầy tại ~u~ sau đó đi đến ~v~. Vậy nên, ta chỉ cần những trạng thái ~j~ hoặc là nằm trong tập ~\{minCost_{u, v}\}~, hoặc là nằm trong tập ~\{t - minCost_{u, v} \}~. Mà ta thấy số lượng phần tử trong của tập ~\{minCost_{u, v}\} \leq 10^4~ (Ta sẽ gọi đây là tập ~j~ đặc biệt).
Chứng minh:
- Xét hai đỉnh đặc biệt (u, v). Ta chia thành ~2~ trường hợp như sau:
- Trường hợp ~1~: ~minCost_u < minCost_v~. Lúc này, để tối ưu, ta nên mua đầy lít xăng (là mua để làm đầy sức chứa) ở tại đỉnh ~u~, sao đó di chuyển đến đỉnh ~v~. Thì chi phí của chúng ta mới tối ưu được (thay vì từ đỉnh ~u~ đi đến đỉnh ~v~ xong rồi mua xăng). (Là cách chuyển trạng thái ~j~ từ ~t \to t - w~)
- Trường hợp ~2~: ~minCost_u > minCost_v~. Lúc này, nếu như trường hợp ta còn đủ lít xăng, ta không nên mua tại ~u~ mà ta đi thẳng đến ~v~ (thì chắc chắn ~f_{v, x}~ không được tính từ ~f_{u, y}~. Trong chiều hướng ngược lại, ta nên mua đủ số lít xăng tại đỉnh ~u~ xong rồi đi đến đỉnh ~v~. (Là cách chuyển trạng thái ~j~ từ ~w \to 0~)
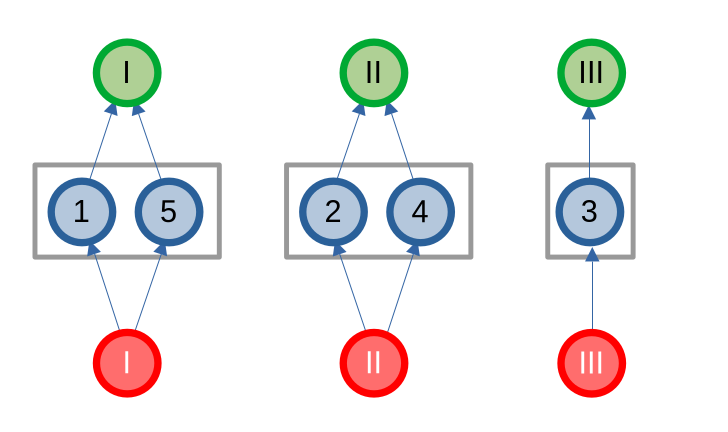
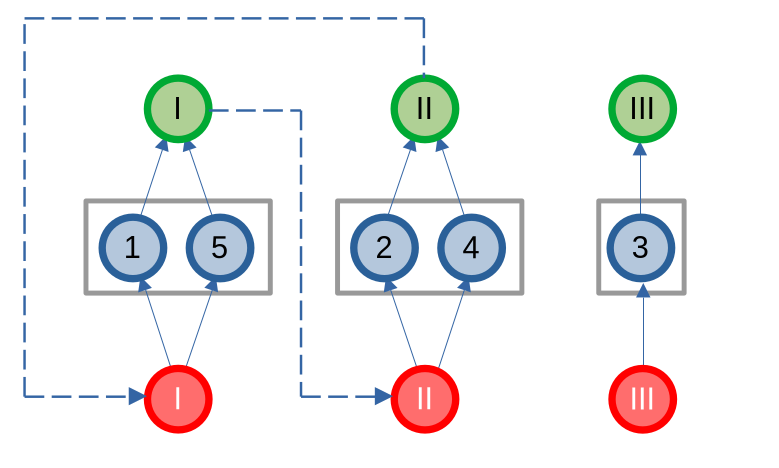
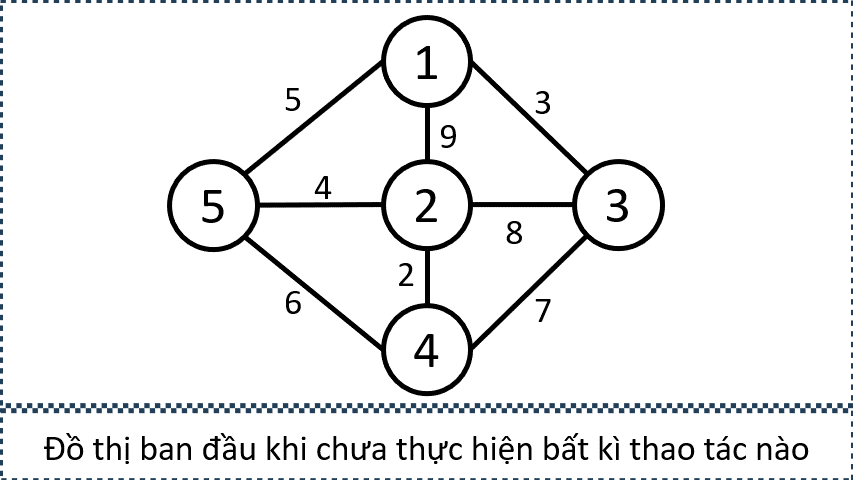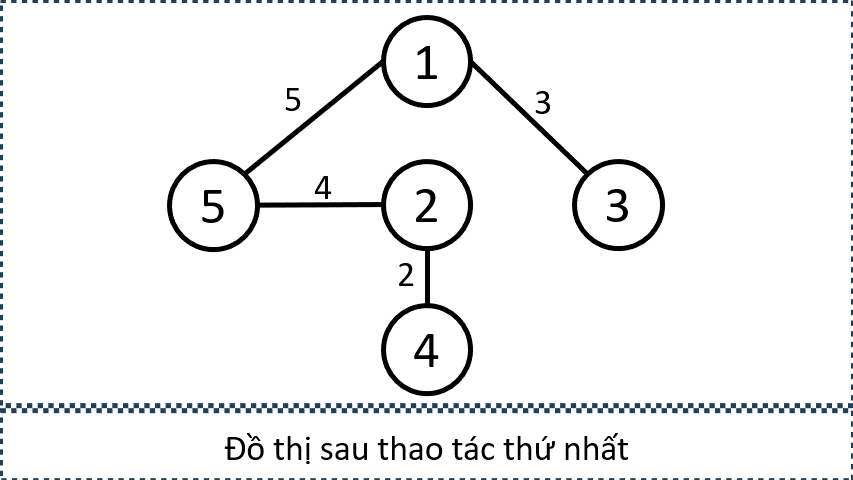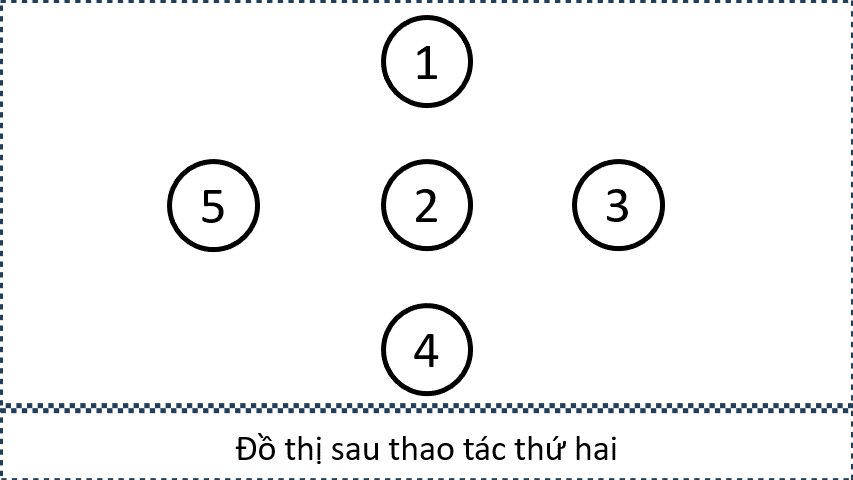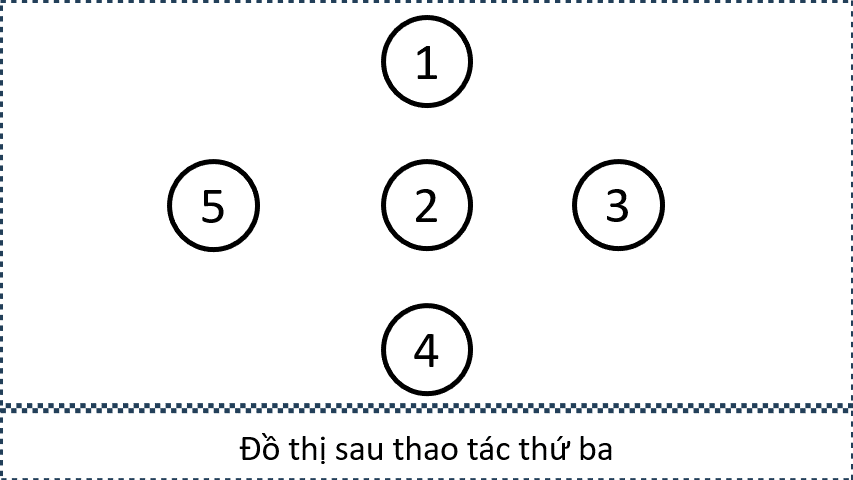
 Xét Sample Input 2 trong đề bài, từ các thông tin sau, ta có thể xây dựng đồ thị như trên:
Xét Sample Input 2 trong đề bài, từ các thông tin sau, ta có thể xây dựng đồ thị như trên:
- ~SpecialNodes = \{ 1,2,3,5 \}~.
- ~SpecialCosts = \{ 0,20,40,60,80,100 \}~.
- Số lít xăng cần ít nhất từ ~1 \to 2~, ~1 \to 3~, ~2 \to 5~ lần lượt là ~80, 40, 80~. Chi phí mua xăng ít nhất tại đỉnh ~1, 2, 3~ lần lượt là ~8, 9, 2~. Ở đồ thị ảo ta xây dựng ở Sample Input 2, đường màu xanh là đường đi tối ưu, chính vì thế kết quả của chúng ta là ~1340~ !
Cuối cùng, ta sẽ có thuật toán như sau: Ta gọi:
- ~specialNodes~, ~specialCosts~ lần lượt là ~i~ và tập ~j~ đặc biệt.
- ~f_{i, j}~ là chi phí thấp nhất để đến đỉnh ~specialNode_i~ và còn dư ~specialCost_j~ lít.
- ~minCost_i~: chi phí nhỏ nhất để mua ~1~ lít xăng tại đỉnh ~specialNode_i~.
- ~minCost_{u, v}~: chi phí để đi từ ~u~ đến ~v~ mà mất ít lít xăng nhất.
Dễ dàng tính được ~minCost{u, v}~ bằng thuật toán dijkstra trên đồ thị ban đầu. Bước tiếp theo, ta sẽ thêm các cạnh vào đồ thị ảo. - Ta sẽ thêm tập cạnh ~f(u, minCost_{u, v}) \to f(v, 0)~ với trọng số là ~0~ nếu ~minCost_{u, v} \leq t~ (với ~u, v~ là những đỉnh đặc biệt) vào đồ thị ảo thể hiện mình sẽ đi đến ~v~ với đủ lít xăng. - Ta tiếp tục thêm tập cạnh ~f(u, t) \to f(v, t - minCost_{u, v})~ với trọng số là ~0~ nếu ~minCost_{u, v} \leq t~ (với ~u, v~ là những đỉnh đặc biệt) vào đồ thị ảo thể hiện mình đi đến ~v~ với đầy lít xăng. - Cuối cùng, ta thêm tập cạnh ~(u, t) \to (u, t')~ với trọng số là ~(t' - t) * minCost_u~ thể hiện ta mua lít xăng tại đỉnh ~u~.
Cuối cùng, ta sử dụng thuật toán dijkstra trong đồ thị ảo để tìm kết quả.
Lời giải #2
Subtask 1
Giới hạn: ~n \le 100~; ~m \le 100~; ~t \le 500~
Ý Tưởng:
- Ta đặt ~\text{costs}[i]~ là chi phí nhỏ nhất để mua ~1~ lít xăng ở thành phố ~i~. Nếu thành phố thứ ~i~ không có trạm xăng nào thì ta có thể coi ~\text{cost}[i] = +\infty~.
- Ta có thể mô hình bài toán bằng cách dựng một đồ thị ~G = (V, E)~ với mỗi đỉnh trong ~G~ đại diện cho một trạng thái của xe, gồm:
- Thành phố xe đang dừng; và
- Lượng xăng xe đang có. Nói cách khác, mỗi đỉnh có thể được biển diễn bằng một cặp số ~(i, f)~ với ~i~ là số hiệu thành phố và ~f~ là lượng xăng hiện tại của xe (~1 \leq i \leq n~, ~0 \leq f \leq t~).
- Ta sẽ có hai loại cạnh dựa trên hai loại hành động:
- Mua ~1~ lít xăng: đồ thị chứa cạnh từ ~(i, f)~ đến ~(i, f + 1)~ (với điều kiện~f < t~) có trọng số ~\text{costs}[i]~.
- Di chuyển sang thành phố khác trên con đường thứ ~i~: đồ thị chứa cạnh từ ~(u_i, r)~ đến ~(v_i, r - w_i)~ (với điều kiện ~r \geq w_i~) có trọng số ~0~.
- Kết quả bài toán ta cần tìm lúc này sẽ tương đương với việc tìm độ dài của đường đi ngắn nhất từ đỉnh ~(st, 0)~ đến một đỉnh ~(en, f)~ bất kì với ~0 \leq f \leq t~. Vì mọi trọng số đều không âm, ta dùng Dijkstra để tìm được độ dài ấy.
Độ Phức Tạp
- Ý tưởng nêu trên có thể được cài đặt với độ phức tạp thời gian ~O((|V| + |E|)\log |V|)~ nếu ta cài đặt thuật toán Dijkstra với heap.
- Vì với mỗi thành phố, ta có ~t + 1~ trạng thái khác nhau đại diện cho các mức xăng khác nhau, ta có ~V = O(n \cdot t)~ .
- Vì với mỗi đường đi, ta sẽ có ~O(t)~ cạnh loại thứ hai được nêu trên và với mỗi thành phố, ta sẽ có ~O(t)~ cạnh loại thứ nhất được nếu trên, ta có ~E = O((n + m) \cdot t)~.
Code Minh Họa:
#include <bits/stdc++.h>
using namespace std;
template<class A, class B>
bool minimize(A &a, const B &b) {
if (a > b) {
a = b;
return true;
}
return false;
}
constexpr int MAX_N = 1'003, MAX_S = 102, MAX_T = 1E5 + 5, INF = 0X3F3F3F3F;
vector<pair<int, int> > graph[MAX_N];
int n, m, s, t, st, en;
signed costs[MAX_N];
void input() {
int u = 0, v = 0, w = 0, p = 0, c = 0;
cin >> n >> m >> s >> t;
for (int i = 1; i <= n; ++i)
costs[i] = INF;
for (int e = 1; e <= m; ++e) {
cin >> u >> v >> w;
graph[u].emplace_back(w, v);
graph[v].emplace_back(w, u);
}
for (int i = 1; i <= s; ++i) {
cin >> p >> c;
minimize(costs[p], c);
}
cin >> st >> en;
}
namespace Dijkstra {
signed minimumCosts[MAX_N][MAX_T];
priority_queue<pair<int, pair<int, int> >, vector<pair<int, pair<int, int> > >, greater<pair<int, pair<int, int> > > > heap;
void considerVertex(const int v, const int r, const int c) {
if (minimize(minimumCosts[v][r], c))
heap.emplace(c, make_pair(v, r));
}
void run() {
memset(minimumCosts, INF, sizeof(minimumCosts));
considerVertex(st, 0, 0);
for (int x = 1; x <= n; ++x)
sort(graph[x].begin(), graph[x].end());
for (; !heap.empty();) {
const auto [m, state] = heap.top();
const auto &[x, r] = state;
heap.pop();
if (minimumCosts[x][r] != m)
continue;
if (x == en) {
cout << m << '\n';
return;
}
for (const auto &[w, y] : graph[x]) {
if (r < w)
break;
considerVertex(y, r - w, minimumCosts[x][r]);
}
if (r + 1 <= t)
considerVertex(x, r + 1, minimumCosts[x][r] + costs[x]);
}
}
}
signed main() {
#ifdef LOCAL
freopen("input.INP", "r", stdin);
#endif // LOCAL
cin.tie(0) -> sync_with_stdio(0);
cout.tie(0);
input();
Dijkstra::run();
return 0;
}
Subtask 2
Giới hạn: ~n \le 1000~; ~m \le 10^4~; ~t \le 500~
Ý Tưởng:
- Vì chương trình giải cần phải chạy trong ~1~ giây (tương đương với khoảng ~10^8~ lệnh), giới hạn của subtask 2 có thể khiến chương trình chạy quá thời gian khi sử dụng thuật toán Dijkstra như trong subtask 1. Một thuật toán thay thế để tìm đường đi ngắn nhất ta có thể sử dụng để tìm đường đi ngắn nhất là SPFA (Shortest Path Faster Algorithm).
Độ Phức Tạp:
- Trong trường hợp tệ nhất, chương trình cài đặt với thuật toán SPFA có thể đạt độ phức tạp thời gian ~O(|V| \cdot |E|)~. Tuy nhiên, thời gian chạy trung bình của SPFA là rất nhanh, có thể được xem như thuật toán chạy với độ phức tạp ~O(|E|)~ trong trường hợp này.
Code Minh Họa:
#include <bits/stdc++.h>
using namespace std;
template<class A, class B>
bool minimize(A &a, const B &b) {
if (a > b) {
a = b;
return true;
}
return false;
}
constexpr int MAX_N = 1'003, MAX_S = 102, MAX_T = 1E5 + 5, INF = 0X3F3F3F3F;
vector<pair<int, int> > graph[MAX_N];
int n, m, s, t, st, en;
signed costs[MAX_N];
void input() {
int u = 0, v = 0, w = 0, p = 0, c = 0;
cin >> n >> m >> s >> t;
for (int i = 1; i <= n; ++i)
costs[i] = INF;
for (int e = 1; e <= m; ++e) {
cin >> u >> v >> w;
graph[u].emplace_back(w, v);
graph[v].emplace_back(w, u);
}
for (int i = 1; i <= s; ++i) {
cin >> p >> c;
minimize(costs[p], c);
}
cin >> st >> en;
}
namespace SPFA {
signed minimumCosts[MAX_N][MAX_T];
bool inqueue[MAX_N][MAX_T];
queue<pair<int, int> > q;
int result = INF;
void considerVertex(const int v, const int r, const int c) {
if (minimize(minimumCosts[v][r], c) && c < result) {
if (v == en)
minimize(result, c);
if (!inqueue[v][r]) {
q.emplace(v, r);
inqueue[v][r] = true;
}
}
}
void run() {
memset(minimumCosts, INF, sizeof(minimumCosts));
considerVertex(st, 0, 0);
for (int x = 1; x <= n; ++x)
sort(graph[x].begin(), graph[x].end());
for (; !q.empty(); q.pop()) {
const auto &[x, r] = q.front();
inqueue[x][r] = false;
for (const auto &[w, y] : graph[x]) {
if (r < w)
break;
considerVertex(y, r - w, minimumCosts[x][r]);
}
if (r + 1 <= t)
considerVertex(x, r + 1, minimumCosts[x][r] + costs[x]);
}
cout << result << '\n';
}
}
signed main() {
#ifdef LOCAL
freopen("input.INP", "r", stdin);
#endif // LOCAL
cin.tie(0) -> sync_with_stdio(0);
cout.tie(0);
input();
SPFA::run();
return 0;
}
Subtask 3
Giới hạn: ~n \le 1000~; ~m \le 10^4~; ~t \le 10^5~
Ý Tưởng:
- Cách dựng đồ thị như trong hai Subtask đầu đều sẽ dẫn đến số lượng đỉnh và cạnh lớn trong Subtask 3 (trong trường hợp tệ nhất, ~|V|~ và ~|E|~ có thể lần lượt đạt khoảng ~10^8~ và hơn ~10^9~).
- Tạm không xét đến chi tiết giá xăng, ta đặt ~G_0 = (V_0, E_0)~ là đồ thị vô hướng có trọng số với mỗi đỉnh đại diện cho một thành phố và mỗi cạnh đại diện cho một đường đi ban đầu (~|V_0| = n~, ~|E_0| = m~).
- Ta nhận thấy rằng không phải thành phố nào cũng có trạm xăng. Vì vậy để giảm số đỉnh cần xem xét, ta có thể mô hình bài toán theo một cách khác như sau:
Ta đặt ~G_1 = (V_1, E_1)~ là một đầy đủ với:
- mỗi đỉnh đại diện cho một thành phố có trạm xăng hoặc là đich đến. ~\Rightarrow |V_1| = O(s)~
- mỗi cạnh có trọng số đại diện cho lượng xăng tối thiểu cần dùng để di chuyển giữa hai đỉnh nếu bình chứa là vô hạn (trọng số này tương đương với đường đi ngắn nhất trong ~G_0~). ~\Rightarrow |E_1| = O(s^2)~
- Nếu ta xét thêm chi tiết giá xăng, ta có thể dựng một đồ thị ~G' = (V', E')~ từ ~G_1~ như cách ta có thể dựng đồ thị ~G~ từ ~G_0~ (bằng cách thêm chi tiết lượng xăng vào trạng thái, ...).
- Khi này, số lượng đỉnh tối đa sẽ được giảm xuống còn khoảng ~10^7~ (~|V'| = O(s \cdot t)~).
- Tuy nhiên, số lượng cạnh vẫn quá lớn để xử lý (~|E'| = O(s^2 \cdot t)~ lớn hơn ~10^9~)
- Để giảm số lượng cạnh cần xét, ta có một số nhận xét như sau:
Trong ~G_1~, xét một cung từ ~x~ tới ~y~ với trọng số ~w~,
- Nếu ~\text{costs}[x] \geq \text{costs}[y]~ hoặc ~y~ là đích đến thì trong ~G'~, ngoại trừ cạnh từ ~(x, w)~ đến ~(y, 0)~, ta không cần phải xem xét bất kì cạnh nào khác giữa từ thành phố ~x~ đến ~y~.
Giải thích:
Trong cả hai trường hợp, ta không có lý do để cần có nhiều hơn ~w~ lít xăng ở thành phố ~x~ bởi:
- Với trường hợp đầu, ta có thể mua xăng với giá rẻ hơn ở thành phố ~y~ (nếu ta không mua xăng ở thành phố ~y~ thì điều này đồng nghĩa với việc, ta muốn đến thành phố khác trong ~V_1~ từ ~x~).
- Với trường hợp sau, ta không đi thêm bất kì đâu khi đã đến đích.
- Nếu ~\text{costs}[x] < \text{costs}[y]~ thì trong ~G'~, ngoại trừ cạnh từ ~(x, t)~ đến ~(y, t - w)~, ta không cần phải xem xét bất kì cạnh nào khác từ thành phố ~x~ đến ~y~.
Giải thích:
Ta không có lý do để cần có ít hơn ~t~ lít xăng ở thành phố ~x~ bởi:
- Nếu ta không mua xăng ở thành phố ~y~ thì điều này đồng nghĩa với việc, ta muốn đến thành phố khác trong ~V_1~ từ ~x~ (vì ~G_1~ là một đồ thị đầy đủ được định nghĩa như trên).
- Nếu ta mua xăng ở thành phố ~y~ nhưng lại rời thành phố ~x~ với lượng xăng không đầy bình, chi phí sẽ không được tối ưu bởi thay vì mua ~1~ lít xăng ở ~y~, ta có thể làm điều tương tự với chi phí rẻ hơn ở thành phố ~x~.
- Với những nhất xét này, số lượng cạnh cần xét sẽ giảm xuống ~|E_2| = O(s^2 + s \cdot t)~ bởi ta chỉ xét tối đa một cạnh giữa hai thành phố khác nhau trong ~G_1~.
Mở rộng:
Số lượng cạnh và đỉnh cần xét có thể tiếp tục được giảm xuống ~O(s^2)~ bằng cách chỉ xét những đỉnh ~(x, f)~ có tối thiểu một cạnh đến đỉnh đại diện cho một thành phố khác ~x~.
Độ Phức Tạp:
- Để dựng được đồ thị ~G_1~, ta có thể cài đặt bằng cách chạy thuật toán Dijkstra nhiều lần với các thành phố có trạm xăng làm đỉnh nguồn. Vì vậy, bước này sẽ có độ phức tạp thời gian ~O(s \cdot n \cdot \log (n + m))~.
- Nếu ta tiếp tục sử dụng thuật toán SPFA trên đồ thị ~G_2 = (V_1, E_2)~, bước tìm kết quả cuối cùng sẽ có độ phức tạp ~O(s^2 + s \cdot t)~. Vì thế độ phức tạp tổng cho các bước xử lý chính có thể được xem như ~O(s \cdot n \cdot \log(n + m) + s^2 + s \cdot t)~.
Code Minh Họa:
#include <bits/stdc++.h>
using namespace std;
template<class A, class B>
bool minimize(A &a, const B &b) {
if (a > b) {
a = b;
return true;
}
return false;
}
constexpr int MAX_N = 1'003, MAX_S = 102, MAX_T = 1E5 + 5, INF = 0X3F3F3F3F;
vector<pair<int, int> > graph[MAX_N];
long long minimumCost = INF;
int n, m, s, t, st, en;
signed costs[MAX_N];
void input() {
int u = 0, v = 0, w = 0, p = 0, c = 0;
cin >> n >> m >> s >> t;
for (int i = 1; i <= n; ++i)
costs[i] = INF;
for (int e = 1; e <= m; ++e) {
cin >> u >> v >> w;
graph[u].emplace_back(w, v);
graph[v].emplace_back(w, u);
}
for (int i = 1; i <= s; ++i) {
cin >> p >> c;
minimize(costs[p], c);
minimize(minimumCost, c);
}
cin >> st >> en;
}
namespace DijkstraAlgorithm {
int vertexCount, vertexID[MAX_N], minimumDistances[MAX_S][MAX_S];
vector<int> vertices, prices;
void findMinimumDistances(const int source) {
priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > heap;
vector<int> distances(n + 1, INF);
heap.emplace(distances[source] = 0, source);
for (; !heap.empty();) {
const auto [d, x] = heap.top();
heap.pop();
for (const auto &[w, y] : graph[x])
if (minimize(distances[y], distances[x] + w))
heap.emplace(distances[y], y);
}
for (const int &destination : vertices)
minimumDistances[vertexID[source]][vertexID[destination]] = distances[destination];
}
void run() {
for (int i = 1; i <= n; ++i)
if (costs[i] < INF || i == en) {
vertexID[i] = (vertexCount++);
vertices.push_back(i);
} else
vertexID[i] = -1;
prices.resize(vertexCount);
for (int i = 0; i < vertexCount; ++i) {
findMinimumDistances(vertices[i]);
prices[i] = costs[vertices[i]];
}
}
}
namespace SPFA {
using namespace DijkstraAlgorithm;
unordered_map<int, unordered_map<int, vector<int> > > graph;
int endVertex, minimumCosts[MAX_S][MAX_T];
bool inqueue[MAX_S][MAX_T];
queue<pair<int, int> > q;
int result = INF;
void considerVertex(const int v, const int r, const int c) {
if (minimize(minimumCosts[v][r], c) && c < result) {
if (v == endVertex)
result = c;
else if (!inqueue[v][r]) {
inqueue[v][r] = true;
q.emplace(v, r);
}
}
}
void buildGraph() {
endVertex = vertexID[en];
for (int x = 0, y = 0; x < vertexCount; ++x)
for (y = 0; y < vertexCount; ++y) {
if (x == y || minimumDistances[x][y] > t)
continue;
if (prices[x] >= prices[y] || y == endVertex) {
graph[x][minimumDistances[x][y]].push_back(y);
continue;
}
graph[x][t].push_back(y);
}
}
void run() {
buildGraph();
memset(minimumCosts, INF, sizeof(minimumCosts));
considerVertex(vertexID[st], 0, 0);
for (; !q.empty(); q.pop()) {
const auto &[x, r] = q.front();
inqueue[x][r] = false;
const auto outerElement = graph.find(x);
if (outerElement != graph.end()) {
const auto &innerElements = (outerElement -> second);
const auto innerElement = innerElements.find(r);
if (innerElement != innerElements.end()) {
for (const auto &y : (innerElement -> second))
considerVertex(y, r - minimumDistances[x][y], minimumCosts[x][r]);
}
}
if (r + 1 <= t)
considerVertex(x, r + 1, minimumCosts[x][r] + prices[x]);
}
cout << result << '\n';
}
}
signed main() {
#ifdef LOCAL
freopen("input.INP", "r", stdin);
#endif // LOCAL
cin.tie(0) -> sync_with_stdio(0);
cout.tie(0);
input();
DijkstraAlgorithm::run();
SPFA::run();
return 0;
}
Xin trân trọng cảm ơn các tác giả đã đồng hành cùng chuyên mục. Các tác giả có bài giải được đăng trong Tạp chí VNOI - Số 1 đã được đội ngũ Tạp chí VNOI liên hệ để nhận phần quà tri ân từ VNOI.
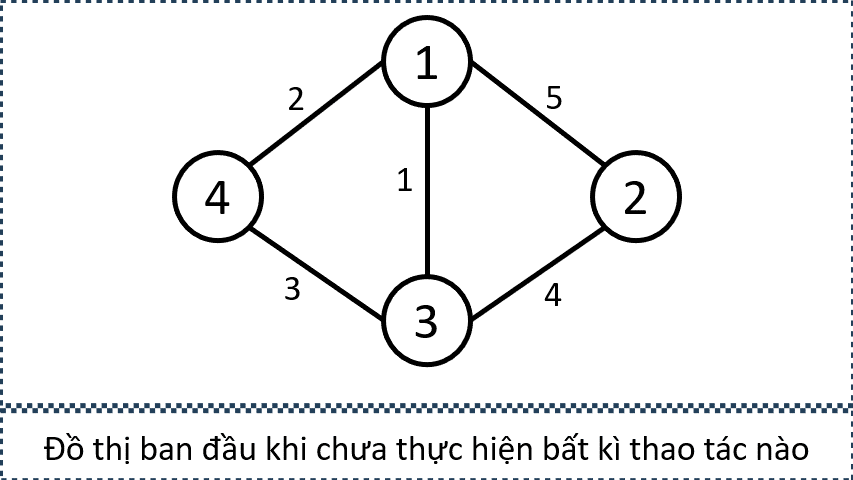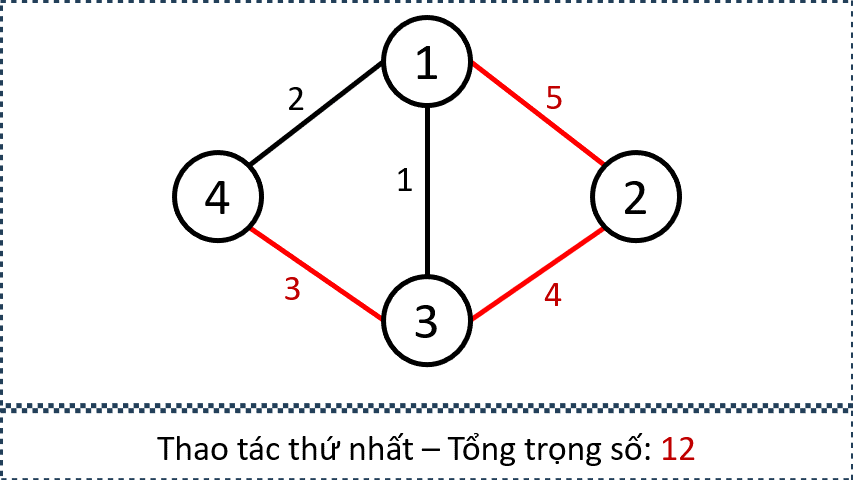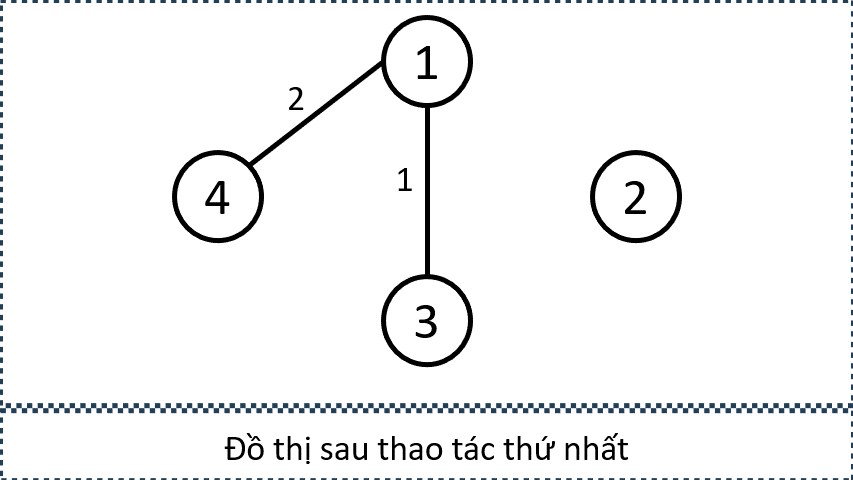
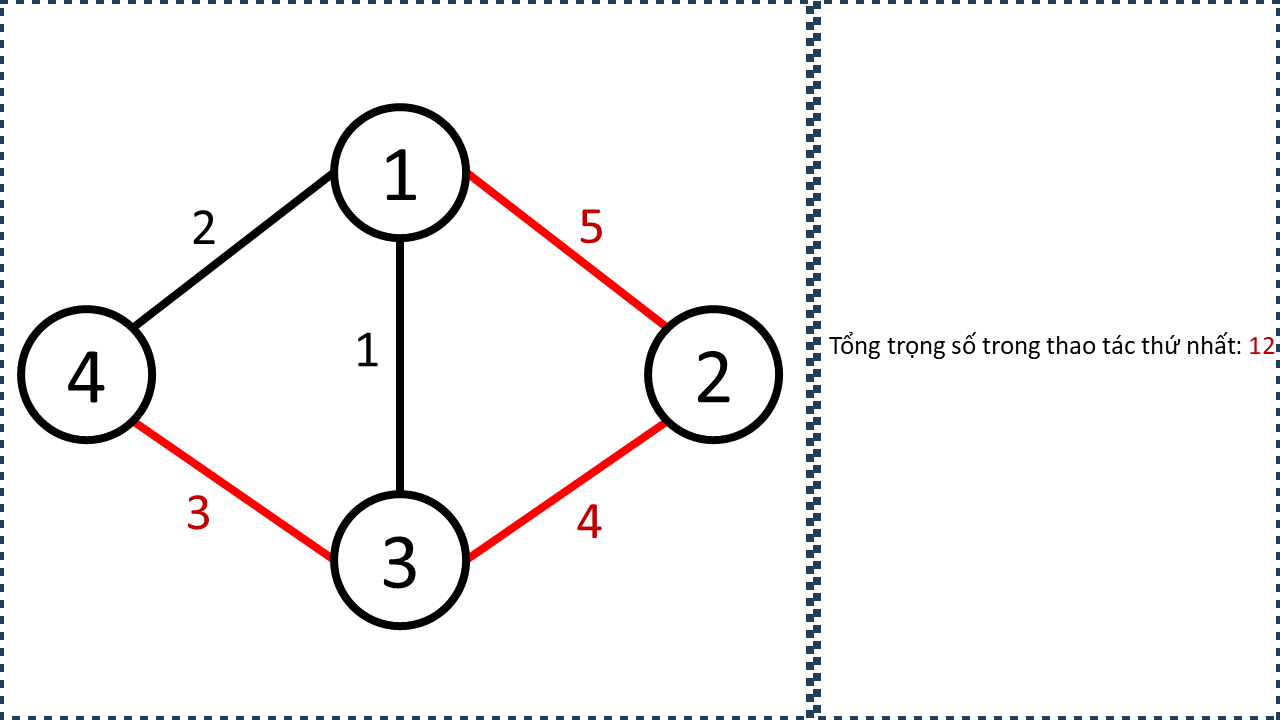


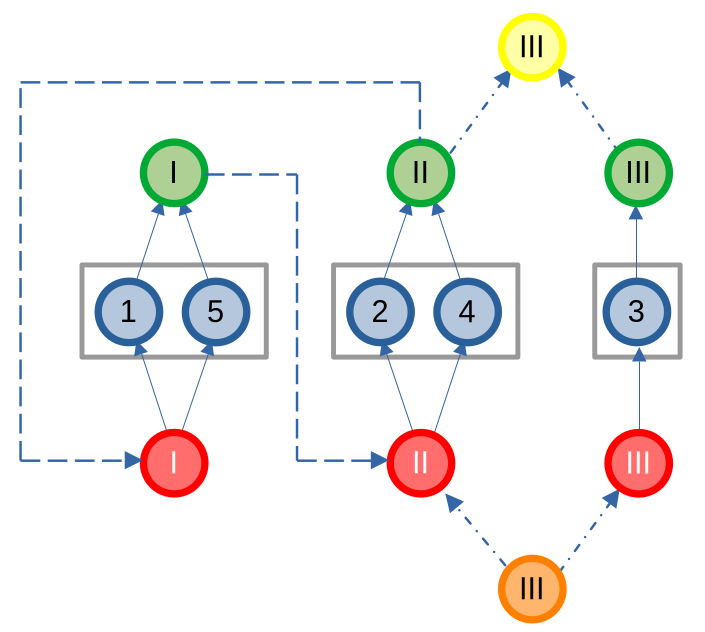
 Giả sử ta cần thêm các cạnh nối từ tất cả các đỉnh xanh đến tất cả các đỉnh cam. Mục tiêu của ta không phải là tạo đủ mọi cạnh giữa hai tập, mà chỉ cần đảm bảo rằng tồn tại đường đi có độ dài 1 từ tập xanh đến tập cam.
Thay vì thêm ~r \times b~ cạnh (với ~r~ là số đỉnh xanh và ~b~ là số đỉnh cam), ta tạo hai đỉnh mới:
Giả sử ta cần thêm các cạnh nối từ tất cả các đỉnh xanh đến tất cả các đỉnh cam. Mục tiêu của ta không phải là tạo đủ mọi cạnh giữa hai tập, mà chỉ cần đảm bảo rằng tồn tại đường đi có độ dài 1 từ tập xanh đến tập cam.
Thay vì thêm ~r \times b~ cạnh (với ~r~ là số đỉnh xanh và ~b~ là số đỉnh cam), ta tạo hai đỉnh mới: