Nguồn dịch - Tác giả: Hydroshiba aka Hải Cẩu

Một trong những bài toán quy hoạch động cơ bản là bài toán tìm dãy con dài nhất (LIS). Chắc hẳn các bạn đã gặp rất nhiều bài toán này dưới các dạng khác nhau. Nhưng nếu chúng ta áp dụng thuật toán này vào việc...sắp xếp thì sẽ thế nào? Hôm nay, mình sẽ giới thiệu cho các bạn thuật toán sắp xếp...LIS.

Ý tưởng thuật toán

Ý tưởng của thuật toán này là ta sẽ tìm dãy con tăng dài nhất rồi đưa nó ra khỏi dãy cho tới khi dãy số ban đầu trống. Ta có thể dễ dàng thấy rằng quá trình này sẽ không lặp vô hạn vì luôn luôn tồn tại dãy con tăng có độ dài là 1, vì thế nên trong mỗi lượt, chúng ta sẽ lấy ra ít nhất một phần tử từ dãy số ban đầu. Để thực hiện thuật toán này, đầu tiên ta sẽ tìm dãy con tăng dài nhất của phần còn lại của dãy ban đầu. Sau đó chúng ta sẽ áp dụng thuật toán sắp xếp LIS cho phần còn lại bằng đệ quy, rồi ghép với dãy tìm được lúc đầu bằng một kỹ thuật giống với thuật toán sắp xếp Merge. Dưới đây là mã giả của thuật toán.

lis_sort(array A){
    find_lis(A);

    array LEFT, RIGHT;
    for(i : elements of A)
        if(i is in LIS) insert i to LEFT;
        else insert i to RIGHT;

    lis_sort(RIGHT);
    merge(LEFT, RIGHT);
}

Để dễ hiều hơn thì bạn có thể theo dõi hình ảnh dưới đây.

Hình ảnh

Điểm yếu của thuật toán này là số lần đệ quy mà nó phải thực hiện. Trong trường hợp xấu nhất thì dãy số ban đầu sẽ ở trạng thái sắp xếp giảm dần và số lần đệ quy ta phải thực hiện sẽ bằng ~N~. Giả sử rằng bạn đang sử dụng thuật toán tìm dãy con tăng dài nhất tiêu chuẩn với độ phức tạp ~O(N^2)~ thì độ phức tạp của thuật toán sắp xếp LIS sẽ là ~O(N^3)~. Bảng dưới đây là thời gian chạy của thuật toán khi áp dụng với các kiểu dãy số khác nhau.

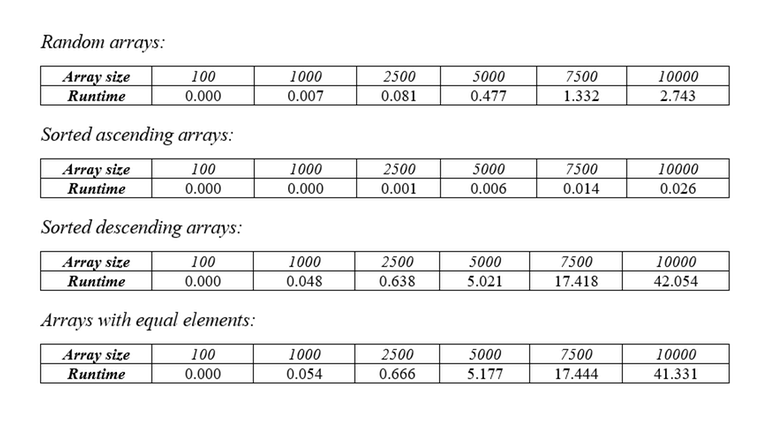
Tối ưu hóa lần 1

Phần chiếm nhiều thời gian nhất của thuật toán là phần tìm dãy con tăng dài nhất với độ phức tạp O(N ^ 2), vì vậy ta nên bắt đầu tối ưu hóa từ đây. Ta có thể tối ưu hóa việc tìm dãy con tăng dài nhất từ ~O(N^2)~ xuống ~O(N*log(N))~ bằng cách kết hợp thêm tìm kiếm nhị phân. Đã có rất nhiều các trang và các bài viết về kỹ thuật này nên các bạn có thể tự mình tìm kiếm trên Google. Đây là bài viết yêu thích của mình.

Ngoài phần tối ưu hoá ở trên, toàn bộ các phần còn lại của code đều được giữ nguyên. Nhờ việc giảm độ phức tạp của thuật toán tìm dãy con tăng dài nhất từ ~O(N^2)~ xuống ~O(N*log(N))~, ta đã giảm độ phức tạp xấu nhất có thể của thuật toán sắp xếp từ ~O(N^3)~ xuống ~O(N^2*log(N))~. Và dưới đây là bảng thống kê thời gian chạy của toán với các kiểu dãy số khác nhau sau khi thực hiện tối ưu hoá lần 1.

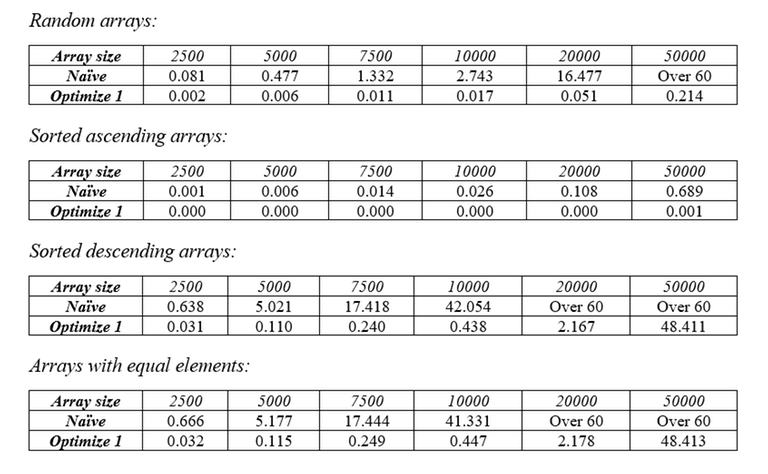
Tối ưu hoá lần 2

Nhìn vào 2 trường hợp cuối, chúng ta có thể thấy rằng khi phải xử lý dãy giảm dần hoặc dãy gồm các số hạng bằng nhau thì hiệu suất sẽ rất thấp. Cộng thêm việc khi tìm kiếm dãy con tăng dài nhất của một dãy số, có khả năng rất cao là những phần tử còn lại sẽ tạo thành một dãy giảm dần (tuy nhiên là không phải lúc nào cũng vậy). Vì vậy, chúng ta có thể đảo ngược dãy số để tăng độ dài dãy con tăng dài nhất tiếp theo. Bằng cách đó, chúng ta có thể tăng tốc thuật toán khi phải thực hiện với những dãy số có các phần tử bằng nhau và dãy số giảm dần. Dưới đây là bảng thời gian chạy của thuật toán khi phải xử lý các loại dãy số khác nhau sau khi tối ưu hoá lần 2.

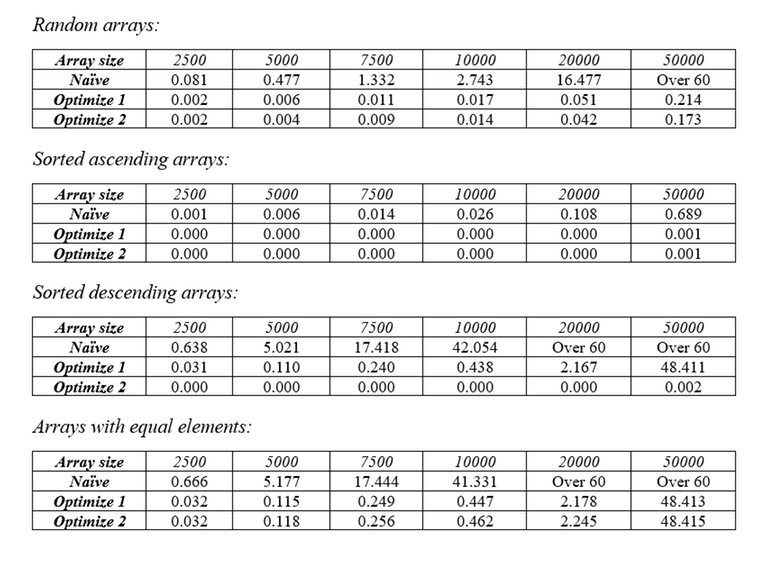
Tối ưu hoá lần 3

Có thể bạn đã nhận ra rằng với những dãy số chứa các phần tử bằng nhau thì hiệu suất của thuật toán sẽ rất thấp. Rất dễ để xử lý vấn đề này, đó là thay vì tìm dãy con tăng dài nhất thì ta sẽ tìm dãy con không giảm dài nhất. Làm thế sẽ đảm bảo rằng tất cả các phần tử bằng nhau sẽ được chọn trong một lượt. Và bất ngờ hơn là làm thế sẽ còn giảm giới hạn dưới của số lần tìm dãy con tăng dài nhất mà ta phải thực hiện.

Bây giờ chúng ta sẽ chứng minh điều này. Gọi số dãy con tăng dài nhất là ~A~ và độ dài dãy con ngắn nhất là ~B~. Bởi vì mỗi lượt duyệt thì dãy số đều được đảo nên chắc chắn rằng dãy con tăng dài nhất sẽ được chọn hoặc mỗi phần tử của dãy con tăng dài nhất đều sẽ được chọn. Vì thế nên dãy con ta chọn trong lượt cuối sẽ là dãy con có độ dài ngắn nhất (giả sử là ta chưa lấy phần tử nào của dãy đó trong các lượt trước), vậy nên số lượt sẽ là ~min(A, B)~.

Bây giờ chúng ta sẽ cố tạo một dãy để ~min(A, B)~ đạt giá trị cực đại. Đầu tiên, ta sẽ cố định giá trị của ~A~ và tăng giá trị ~B~ theo ~A~. Ta có:

~N = L_1 + L_2 + … + L_A~

Trong đẳng thức trên, ~L_i~ là độ dài của dãy con tăng thứ ~i~. Ta lấy ~L_k~ là độ dài dãy con tăng ngắn nhất, ta có:

~L_k \leq L_i (\forall i \in [1, N])~

~\Rightarrow L_1 + L_2 + … + L_A \geq L_k + L_k + … + L_k (A lần)~

~\Rightarrow N \geq A * B~

Vậy ~B~ lớn nhất khi ~N = A * B~. Và từ đẳng thức mới rút gọn ở trên, ta dễ dàng chứng minh được rằng giá trị lớn nhất của ~min(A, B)~ là ~sqrt(N)~. Vì mỗi lượt ta cần duyệt 2 lần, một lần là để lấy dãy con tăng dài nhất, một lần để lấy một phần tử của mỗi dãy con tăng nên số lượt duyệt sẽ không thể quá ~2 * sqrt(N)~. Vì vậy nên độ phức tạp của thuật toán này sẽ là ~O(N * sqrt(N) * log(N))~. Tất nhiên đó chỉ là giả thuyết, bây giờ chúng ta hãy xem thuật toán này đã được tối ưu hoá thế nào. Dưới đây là bảng thời gian chạy của thuật toán khi phải xử lý các loại dãy số khác nhau sau khi tối ưu hoá lần 3.

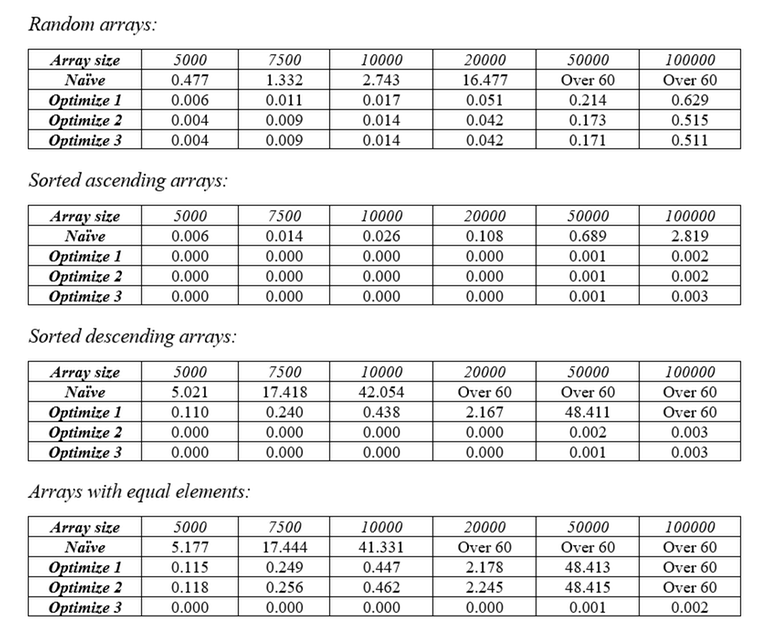
Ta thấy là thời gian xử lý các trường hợp đặc biệt đã được giảm đi rất nhiều. Bây giờ chúng ta sẽ thử so sánh với các thuật toán sắp xếp khác.

Mặc dù đã nhanh hơn rất nhiều so với thuật toán lúc ban đầu, nhưng khi so sánh với các thuật toán khác thì nó vẫn còn rất kém do phải thực hiện thêm ~sqrt(N)~ phép toán mỗi lần tìm dãy con tăng dài nhất, trong khi các thuật toán khác chỉ cần ~O(N*log(N))~.

Chi tiết kĩ thuật

Tất cả các test trong bài đăng này đều được thực hiện với bộ xử lý i7-1165G7 chạy ở 3,30 GHz với 16 GB RAM. Tất cả các test case đều được sinh ngẫu nhiên và thống nhất trong phạm vi ~[1, 1e6]~ bằng cách sử dụng thư viện testlib.h. Chương trình test được chạy trên Code::Blocks 20.03, sử dụng trình biên dịch C++ 14 và thời gian thực hiện được tính bằng giây. Các bài test được thực hiện 20 lần và giá trị cuối cùng được lấy từ giá trị trung bình của 20 giá trị của 20 lần chạy trên.

Tổng kết

Thành thực mà nói thì mình thấy rằng thuật toán này gần như không có tính thực tiễn. Có rất nhiều thuật toán sắp xếp khác vừa nhanh lại vừa tiết kiệm bộ nhớ hơn thuật toán này. Tuy nhiên là trong khi tìm hiểu về thuật toán này thì mình đã học được rất nhiều thứ, đặc biệt là bất đẳng thức.

^{P/s: Hải cẩu orz!}