Kỳ thi Học sinh giỏi Quốc gia 2025 - Ngày 1
Điểm: 7
Ở một quốc gia nọ có ~N~ hòn đảo, được đánh số lần lượt từ ~1~ đến ~N~. Có ~N - 1~ cây cầu, mỗi cây cầu nối trực tiếp ~2~ hòn đảo tạo thành một quần thể đảo mà giữa hai hòn đảo bất kỳ luôn tồn tại đường đi thông qua một cây cầu hoặc một dãy các cây cầu.
Tuấn là một người giao hàng của công ty VOI. Bạn đầu Tuấn ở hòn đảo ~1~, được giao ~K~ nhiệm vụ giao hàng theo thứ tự từ ~1~ đến ~K~ và Tuấn phải xử lý các nhiệm vụ theo đúng thứ tự đó. Với nhiệm vụ thứ ~i~ (~1 \leq i \leq K~), Tuấn cần thực hiện giao hàng từ hòn đảo ~U_i~ đến hòn đảo ~V_i~ theo đường đi ghé qua ít hòn đảo nhất. Tuấn chỉ có thể thực hiện nhiệm vụ giao hàng thứ ~i~ nếu vị trí của Tuấn đang ở ~U_i~ và sau khi hoàn thành giao hàng thì vị trí của Tuấn sẽ là ~V_i~. Lưu ý đối với mỗi nhiệm vụ, Tuấn có thể thực hiện hoặc từ chối giao hàng. Đối với mỗi hòn đảo, công ty sẽ đặt một giá trị phần thưởng mà người giao hàng có thể nhận được cho mỗi lần ghé qua. Với mỗi nhiệm vụ hoàn thành, Tuấn sẽ nhận được phần thưởng là giá trị lớn nhất trong số các giá trị của các hòn đảo nằm trên đường đi giao hàng, tính cả hòn đảo xuất phát và hòn đảo kết thúc.
Yêu cầu: Hãy tính tổng giá trị phần thưởng lớn nhất mà Tuấn có thể nhận được sau ~K~ nhiệm vụ.
Input
Vào từ file văn bản SHIP.INP:
Dòng đầu chứa một số nguyên ~N~ là số lượng hòn đảo (~1 \leq N \leq 2 \times 10^5~).
Dòng thứ hai chứa ~N~ số nguyên ~W_1, W_2, \dots, W_N~ là giá trị phần thưởng tại các hòn đảo (~0 \leq W_1, W_2, \dots, W_N \leq 10^9~).
Mỗi dòng trong số ~N - 1~ dòng tiếp theo chứa 2 số nguyên dương thể hiện cây cầu kết nối giữa 2 hòn đảo.
Dòng tiếp theo chứa một số nguyên ~K~ là số lượng nhiệm vụ (~1 \leq K \leq 2 \times 10^5~).
Dòng thứ ~i~ trong số ~K~ dòng tiếp theo chứa 2 số nguyên ~U_i~ và ~V_i~ thể hiện nhiệm vụ giao hàng thứ ~i~ (~1 \leq U_i, V_i \leq N; U_i \neq V_i~).
Các số trên cùng một dòng cách nhau bởi dấu cách.
Output
Ghi ra file văn bản SHIP.OUT:
- Một số nguyên duy nhất thể hiện tổng giá trị phần thưởng lớn nhất mà Tuấn có thể nhận được sau ~K~ nhiệm vụ.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~20\%~ | ~N, K \leq 100~ và hòn đảo ~i~ có cây cầu nối với hòn đảo ~i + 1~ (~\forall i : 1 \leq i \leq N - 1~) |
| 2 | ~20\%~ | ~N \leq 10000~, ~K \leq 100~ và hòn đảo ~i~ có cây cầu nối với hòn đảo ~i + 1~ (~\forall i : 1 \leq i \leq N - 1~) |
| 3 | ~20\%~ | Hòn đảo ~i~ có cây cầu nối với hòn đảo ~i + 1~ (~\forall i : 1 \leq i \leq N - 1~) |
| 4 | ~20\%~ | ~N \leq 10000~ và ~K \leq 100~ |
| 5 | ~20\%~ | Không có ràng buộc nào thêm. |
Sample Input 1
4
1 2 3 4
1 2
2 3
3 4
4
1 3
1 2
2 3
2 4
Sample Output 1
6
Sample Input 2
7
1 5 5 7 3 16 1
1 4
1 2
2 3
4 5
5 6
5 7
7
1 3
3 2
1 4
4 2
2 5
5 7
5 6
Sample Output 2
37
Điểm: 7
Trong cuộc thi trí tuệ nhân tạo ROAI2025, Ban tổ chức yêu cầu các đội chơi lập trình Robot AI trên sân đấu trong môi trường thực tế ảo tham chiếu trên hệ trục tọa độ ~Oxy~. Mỗi đội chơi cần đặt 2 con Robot AI tại 2 điểm phân biệt trên đường thẳng ~y = 2~ với tọa độ ~x~ là số nguyên trong phạm vi từ 0 tới ~N~. Mỗi Robot AI có một mắt thần có nhiệm vụ quan sát đường thẳng ~y = 0~. Sàn đấu có hai tấm chắn biên là các đoạn thẳng ~AB~ và ~CD~ với tọa độ: ~A(0,2)~, ~B(0,1)~, ~C(N,1)~, ~D(N,2)~. Ban tổ chức đặt thêm ~K~ tấm chắn khác là những đoạn thẳng nằm trên đoạn ~BC~. Tấm chắn thứ ~i~ trong số ~K~ tấm chắn bắt đầu từ điểm ~(L_i,1)~ và kết thúc ở điểm ~(R_i,1)~. Robot AI tại điểm ~U~ trên đường thẳng ~y = 2~ chỉ quan sát được những điểm ~V~ trên đường thẳng ~y = 0~ nếu như đoạn thẳng ~UV~ không giao với bất kỳ đoạn thẳng là tấm chắn nào trong số ~K + 2~ tấm chắn trên. Một đoạn trên đường thẳng ~y = 0~ gọi là quan sát được nếu như mọi điểm trên đoạn đó (ngoại trừ 2 đầu mút) đều quan sát được. Nhiệm vụ của mỗi đội chơi là cần đặt được 2 con Robot AI sao cho tổng độ dài các đoạn quan sát được trên đường thẳng ~y = 0~ bởi ít nhất một Robot AI là lớn nhất có thể.
Yêu cầu: Đội tuyển của Tuấn lần đầu tiên tham gia thi tài, hãy giúp đội của Tuấn tìm ra cách đặt tối ưu cho 2 con Robot AI.
Input
Vào từ file văn bản ROAI.INP:
Dòng đầu chứa hai số nguyên ~N~ và ~K~ ~(1 \le N \le 10^9; 1 \le K \le 2000)~.
Dòng thứ ~i~ trong số ~K~ dòng tiếp theo chứa hai số nguyên ~L_i~ và ~R_i~ ~(0 \le L_i \lt R_i \le N)~.
Dữ liệu bảo đảm ~L_1 \lt R_1 \lt L_2 \lt R_2 \lt \ldots \lt L_K \lt R_K~. Các số trên cùng một dòng cách nhau bởi dấu cách.
Output
Ghi ra file văn bản ROAI.OUT:
- Một số nguyên duy nhất là tổng độ dài các đoạn quan sát được trên đường thẳng ~y = 0~ trong phương án tối ưu tìm được.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~16\%~ | ~N \le 200~ |
| 2 | ~16\%~ | ~N \le 2000; K \le 20~ |
| 3 | ~20\%~ | ~N \le 20000~ |
| 4 | ~20\%~ | ~K \le 500~ |
| 5 | ~28\%~ | Không có ràng buộc nào thêm |
Sample Input 1
3 1
0 1
Sample Output 1
7
Sample Input 2
5 2
1 2
3 5
Sample Output 2
8
Notes
Trong ví dụ 1, một phương án đặt vị trí tối ưu cho 2 Robot AI là ~x = 0~ và ~x = 3~. Robot AI thứ nhất quan sát được đoạn ~[2, 6]~; Robot AI thứ hai quan sát được đoạn ~[-1, 3]~.
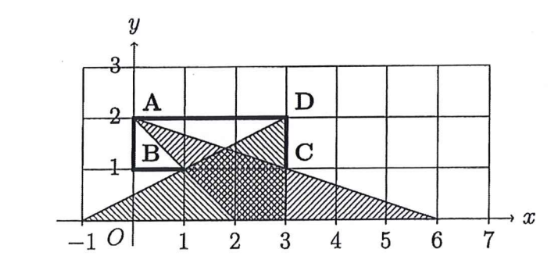
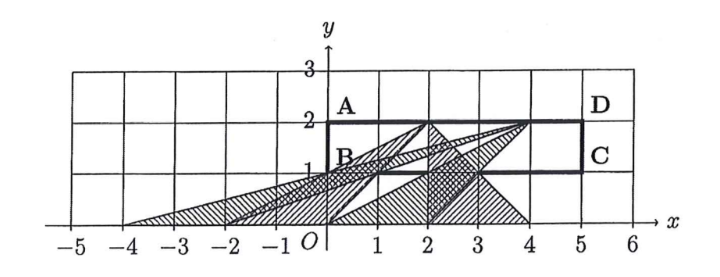
Trong ví dụ 2, một phương án đặt vị trí tối ưu cho 2 Robot AI là ~x = 2~ và ~x = 4~. Robot AI thứ nhất quan sát được đoạn ~[-2, 0]~ và đoạn ~[2, 4]~; Robot AI thứ hai quan sát được đoạn ~[-4, 2]~ và đoạn ~[0, 2]~.
Điểm: 6
Thầy giáo Lê rất yêu thích các bài toán số học và dãy số. Thầy định nghĩa trọng số của một số nguyên dương ~X~ (ký hiệu là ~W(X)~) như sau:
Đầu tiên, thầy Lê biểu diễn ~X~ thành dãy các chữ số của nó trong hệ cơ số 10, thu được dãy ~X_1, X_2, \ldots, X_N~ với ~N~ là số chữ số của ~X~;
Nếu dãy chữ số của ~X~ có chứa hai phần tử đứng cạnh nhau có tổng chia hết cho 5, nghĩa là tồn tại ~i \in \{1, 2, \ldots, N - 1\}~ sao cho ~(X_i + X_{i+1}) \mod 5 = 0~, thì ~W(X) = 0~;
Ngược lại, ~W(X)~ chính là số lượng dãy con gồm các phần tử liên tiếp trong dãy chữ số của ~X~ mà có kết quả XOR các phần tử bằng 0. Cụ thể, ~W(X)~ là số lượng cặp ~(i, j)~ thoả mãn ~1 \leq i \leq j \leq N~ và ~X_i \oplus X_{i+1} \oplus \ldots \oplus X_j = 0~, với ~\oplus~ là phép toán XOR giữa hai số tự nhiên.
Nhắc lại, với hai số tự nhiên ~a~ và ~b~, phép toán ~a \oplus b~ là phép toán XOR từng bit tương ứng của ~a~ và ~b~ trong biểu diễn hệ nhị phân của chúng.
Ví dụ:
~W(1234) = 0~ vì chứa hai chữ số 2 và 3 cạnh nhau có tổng chia hết cho 5;
~W(122103) = 5~ vì không có hai chữ số nào cạnh nhau có tổng chia hết cho 5, đồng thời dãy chữ số của nó có 5 dãy con gồm các phần tử liên tiếp là ~(2, 2)~, ~(1, 2, 2, 1)~, ~(1, 2, 2, 1, 0)~, ~(0)~ và ~(2, 1, 0, 3)~ có XOR các phần tử bằng 0;
~W(3456) = 0~ vì dãy chữ số của nó không có dãy con nào có XOR các phần tử bằng 0.
Yêu cầu: Cho số nguyên dương ~k~ và các số nguyên dương ~L, H~. Hãy tính tổng lũy thừa ~k~ của trọng số của tất cả các số nguyên dương nằm trong phạm vi ~[L, H]~, nghĩa là tính ~\sum_{X=L}^H (W(X))^k~.
Input
Vào từ file văn bản PNUM.INP:
Dòng đầu chứa một số nguyên dương ~k~ là số lũy thừa trong tổng cần tính ~(1 \leq k \leq 2)~.
Dòng thứ hai chứa một số nguyên dương ~T~ là số lượng trường hợp test ~(1 \leq T \leq 50\,000)~.
Mỗi dòng trong số ~T~ dòng tiếp theo chứa hai số nguyên dương ~L~ và ~H~ mô tả một trường hợp test ~(1 \leq L \leq H \leq 10^{1000})~.
Dữ liệu bảo đảm tổng số chữ số của tất cả các số ~L~ và ~H~ trong một file dữ liệu vào không vượt quá ~10^5~. Các số trên cùng một dòng cách nhau bởi dấu cách.
Output
Ghi ra file văn bản PNUM.OUT:
- Gồm ~T~ dòng, mỗi dòng chứa một số nguyên là phần dư của kết quả tìm được trong phép chia cho ~1\,000\,000\,007~ tương ứng với trường hợp test trong dữ liệu đầu vào.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~12\%~ | ~T \leq 10~ và ~H \leq 10^6~ |
| 2 | ~12\%~ | ~T \leq 10~; ~H \leq 10^{18}~ và ~k = 1~ |
| 3 | ~12\%~ | ~H \leq 10^{18}~ và ~k = 1~ |
| 4 | ~12\%~ | ~k = 1~ |
| 5 | ~20\%~ | ~T \leq 10~; ~H \leq 10^9~ và ~k = 2~ |
| 6 | ~16\%~ | ~L~ là luỹ thừa của 10; ~H = 10 \times L - 1~ và ~k = 2~ |
| 7 | ~16\%~ | Không có ràng buộc nào thêm |
Sample Input 1
1
3
1 10
100 105
111239 111245
Sample Output 1
1
5
12
Sample Input 2
2
3
1 10
100 105
111239 111245
Sample Output 2
1
7
30
Notes
Trong ví dụ thứ nhất:
Trường hợp test thứ nhất: ~W(1) = W(2) = W(3) = W(4) = W(5) = W(6) = W(7) = W(8) = W(9) = 0~, ~W(10) = 1~, nên kết quả là ~0^1 + 0^1 + 0^1 + 0^1 + 0^1 + 0^1 + 0^1 + 0^1 + 0^1 + 1^1 = 1~.
Trường hợp test thứ hai: ~W(100) = 0~, ~W(101) = 2~, ~W(102) = 1~, ~W(103) = 1~, ~W(104) = 1~, ~W(105) = 0~, nên kết quả là ~0^1 + 2^1 + 1^1 + 1^1 + 1^1 + 0^1 = 5~.
Trường hợp test thứ ba: ~W(111239) = 0~, ~W(111240) = 3~, ~W(111241) = 0~, ~W(111242) = 2~, ~W(111243) = 2~, ~W(111244) = 3~, ~W(111245) = 2~, nên kết quả là ~0^1 + 3^1 + 0^1 + 2^1 + 3^1 + 2^1 = 12~.
Trong ví dụ thứ hai:
Trường hợp test thứ nhất: Kết quả là ~0^2 + 0^2 + 0^2 + 0^2 + 0^2 + 0^2 + 0^2 + 0^2 + 0^2 + 1^2 = 1~.
Trường hợp test thứ hai: Kết quả là ~0^2 + 2^2 + 1^2 + 1^2 + 1^2 + 0^2 = 7~.
Trường hợp test thứ ba: Kết quả là ~0^2 + 3^2 + 0^2 + 2^2 + 3^2 + 2^2 = 30~.