Nodel sắp tới, Ông Già Tuyết đã chuẩn bị ~2n~ món quà cho các bạn nhỏ. Các món quà có màu sắc đôi một khác nhau và có mã màu từ ~1~ đến ~2n~. Khi cho các món quà vào túi, Ông đã đưa ra các món quà vào theo một thứ tự mà nếu lấy ra, các món quà sẽ có mã màu lần lượt là ~c_1, c_2, \dotsc, c_{2n}~ (dãy ~c_1, c_2,\dotsc, c_{2n}~ là một hoán vị của ~1, 2, \dotsc, 2n~).

Ông Già Tuyết dự định tặng quà cho ~m (m \le n)~ bạn nhỏ, mỗi bạn sẽ dược nhận hai món quà sau hai lượt tặng. Các bạn nhỏ đứng thành một hàng và Ông sẽ đi từ đầu hàng đến cuối hàng để lần lượt tặng quà cho từng bạn. Khi đứng trước một bạn nhỏ để tặng quà, Ông lần lượt lấy từng món quà ra cho tới khi lựa chọn được một món quà phù hợp và tặng bạn nhỏ, các món quà không được lựa chọn sẽ được cất đi và không được dùng để tặng quà. Khi bạn nhỏ thứ ~m~ ở cuối hàng đã được nhận quà, Ông sẽ di chuyển về đầu hàng để tặng quà lượt thứ hai tương tự như lượt thứ nhất.

Ông được biết, các bạn nhỏ luôn mong muốn nhận được hai món quà mà chênh lệch mã màu của hai món quà đó không vượt quá ~d~. Với mong muốn mang lại nhiều niềm vui cho các bạn nhỏ, Ông quyết định việc tặng quà sẽ phải đảm bảo tất cả các bạn nhỏ đều nhận được hai món quà mà chênh lệch mã màu không vượt quá ~d~.

Một cách hình thức, gọi ~m~ là số lượng bạn nhỏ được quà, Ông cần chọn ra dãy ~2m~ chỉ số ~1 \le i_1 < i2 < \dotsc < i_m < i_{m + 1} < \dotsc i_{2m} \le 2n~ sao cho ~\left|c_{i_k} - c_{i_{m + k}}\right| \le d~ với mọi ~1 \le k \le m~.

Ông Già Tuyết biết rằng, có thể không tồn tại cách chọn được ~2m~ chỉ số thỏa mãn, điều đó cũng có nghĩa là không thể tặng quà như mong muốn cho cả ~m~ bạn nhỏ. Do đó, với một số nguyên dương ~d~ và thứ tự các món quà lấy ra có mã màu lần lượt là ~c_1, c_2, \dotsc, c_{2m}~, Ông muốn tính số lượng nhiều nhất các bạn nhỏ mà Ông có thể tặng quà.

Yêu cầu: Hãy giúp Ông Già Tuyết tính số lượng nhiều nhất các bạn nhỏ mà Ông có thể tặng quà đáp ứng điều kiện nêu trên.

Dữ liệu

Vào từ đầu vào chuẩn (không phải từ file NOEL.INP):

• Dòng thứ nhất chứa hai số nguyên dương ~n~ và ~d (d \le 5)~.
• Dòng thứ hai chứa ~2n~ số nguyên dương ~c_1, c_2, \dotsc, c_{2n}~ là mã màu của các món quà lần lượt được lấy ra.

Các số trên cùng một dòng cách nhau bởi dấu cách.

Kết quả

Ghi ra đầu ra chuẩn (không phải ra file NOEL.OUT) một số nguyên duy nhất là số lượng nhiều nhất các bạn nhỏ mà Ông Già Tuyết có thể tặng quà.

Ràng buộc

• Có ~40\%~ số test tương ứng với ~40\%~ số điể của bài thỏa mãn ~n \le 10~;
• ~40\%~ số test khác ứng với ~40\%~ số điểm của bài thỏa mãn ~n \le 100~;
• ~20\%~ số test còn lại ứng với ~20\%~ số điểm của bài thỏa mãn ~n \le 1000~.

Ví dụ

Input

3 1
1 5 6 3 4 2

Output

2

Giải thích

Ông Già Tuyết có thể tặng tối đa cho 2 bạn nhỏ.

• Lượt thứ nhất, món quà có mã màu 5 tặng bạn thứ nhất, món quà có mã màu 3 tặng bạn thứ hai.
• Lượt thứ hai, món quà có mã màu 4 tặng bạn thứ nhất và món quà có mã màu 2 tặng bạn thứ hai.

Một ngân hàng có ~n~ chi nhánh, mỗi chi nhánh có một máy chủ, các máy chủ ở các chi nhánh được đánh số từ ~1~ đến ~n~. Nhằm bảo đảm việc truyền thông giữa các chi nhánh, ngân hàng đã thuê ~n - 1~ kênh truyền tin trực tiếp từ một nhà máy cung cấp dịch vụ mạng để kết nối ~n~ máy chủ thành một mạng máy tính và bảo đảm từ máy chủ của một chi nhánh bất kì có thể truyền tin đến tất cả các máy chủ của các chi nhánh còn lại theo kênh truyền tin trực tiếp giữa chúng hoặc thông qua đường truyền đi qua một số máy chủ của các chi nhánh nào đó.

Trong thời gian tới, ngân hàng muốn lựa chọn ~k~ máy chủ trong ~n~ máy chủ để cài đặt phần mềm kiểm soát. Phần mềm khi hoạt động sẽ làm tăng lưu lượng truyền trên các kênh giữa ~k~ máy chủ này. Với mỗi phương án chọn ~k~ máy chủ để cài đặt phần mềm, trong số ~n - 1~ kênh truyền tin, nhà cung cấp dịch vụ mạng đã xác định một số ít nhất các kênh đủ để kết nối ~k~ máy chủ này và khuyến cáo ngân hàng cần phải nâng cấp các kênh đó. Vì lí do kĩ thuật cũng như kinh phí, ngân hàng muốn lựa chọn ~k~ máy chú để cài đặt phần mềm mà số lượng kênh ít nhất cần nâng cấp có giá trị nằm trong đoạn ~[a, b]~. Cụ thể, với một cách chọn ~k~ máy chủ, gọi ~s~ là số kênh ít nhất cần chọn ra trong ~n - 1~ kênh truyền tin nhằm bảo đảm liên thông giữa ~k~ máy chủ được chọn ngay cả khi các kênh còn lại bị đứt kết nối, ~s~ kênh này sẽ được khuyến cáo nâng cấp, khi đó, cách chọn ~k~ máy chủ thỏa mãn yêu cầu của ngân hàng nếu ~a \le s \le b~.

Yêu cầu: Cho ~n - 1~ kênh truyền tin và các giá trị ~k, a, b~, hãy đếm số lượng cách chọn ~k~ máy chủ để cài đặt phần mềm mà số lượng kênh ít nhất cần nâng cấp nằm trong đoạn ~[a, b]~.

Dữ liệu

Vào từ đầu vào chuẩn (không phải file COMNET.INP):

• Dòng thứ nhất chứa bốn số nguyên dương ~n, k, a, b (k < n; 1 < a \le b < n)~;
• Dòng thứ i trong số ~n - 1~ dòng tiếp theo chứa 2 số nguyên dương ~u_i, v_i~ cho biết có kênh truyền tin trực tiếp giữa hai máy chủ ~u_i, v_i (1 \le u_i, v_i \le n, u_i \ne v_i)~.

Các số trên cùng một dòng cách nhau bởi dấu cách.

Kết quả

Ghi ra đầu ra chuẩn (không phải file COMNET.OUT) một số nguyên duy nhất là số cách chọn ~k~ máy chủ để cài đặt phần mềm thỏa mãn yêu cầu của ngân hàng.

Ràng buộc

• ~20\%~ số test tương ứng với ~20\%~ số điểm của đề bài thỏa mãn: ~n \le 100~ và ~k = 2~;
• ~30\%~ số test khác tương ứng với ~30\%~ số điểm của đề bài thỏa mãn: ~n \le 100~ và ~k = 3~;
• ~20\%~ số test khác tương ứng với ~20\%~ số điểm của đề bài thỏa mãn: ~n \le 100~ và ~k = 4~;
• ~20\%~ số test khác tương ứng với ~20\%~ số điểm của đề bài thỏa mãn: ~n \le 1000~ và ~k = 3~;
• ~10\%~ số test còn lại ứng với ~10\%~ số điểm của đề bài thỏa mãn: ~n \le 1000~ và ~k = 4~;

Ví dụ

Input

6 3 2 3
1 2
2 3
3 4
4 5
3 6

Output

14

Giải thích

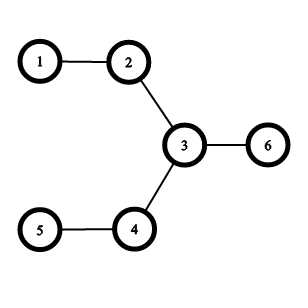
Có 5 cách chọn 3 máy chủ trong 6 máy chủ mà số kênh cần nâng cấp bằng 2 là:

1. ~(1, 2, 3)~;
2. ~(2, 3, 4)~;
3. ~(2, 3, 6)~;
4. ~(3, 4, 5)~;
5. ~(3, 4, 6)~;

Có 9 cách chọn 3 máy chủ trong 6 máy chủ mà số kênh cần nâng cấp bằng 3 là:

1. ~(1, 2, 4)~;
2. ~(1, 2, 6)~;
3. ~(1, 3, 4)~;
4. ~(1, 3, 6)~;
5. ~(2, 3, 5)~;
6. ~(2, 4, 5)~;
7. ~(2, 4, 6)~;
8. ~(3, 5, 6)~;
9. ~(4, 5, 6)~;

Như vậy có tất cả 14 cách chọn 3 máy chủ trong 6 máy chủ thỏa mãn yêu cầu của ngân hàng.

Nội dung chính trong tiết học Tin học trên lớp của Nam ngày hôm nay là về phép toán OR. Phép toán OR (có kí hiệu là |) được định nghĩa như sau: Kết quả của phép toán OR giữa 2 số nguyên không âm ~x~ và ~y~ là một số nguyên không âm ~z~ trong đó bit thứ ~i~ trong biểu diễn nhị phân của ~z~ sẽ là ~0~ khi và chỉ khi bit thứ ~i~ trong biểu diễn nhị phân của ~x~ và ~y~ đồng thời bằng ~0~, ngược lại bit thứ ~i~ trong biểu diễn nhị phân của ~z~ là ~1~.

Ví dụ, ~x = 12~ có biểu diễn nhị phân là 1100, ~y = 5~ có biểu diễn nhị phân là 0101, khi đó ~x | y~ có biểu diễn nhị phân là 1101, tức giá trị ~13~ trong hệ cơ số thập phân.

Phép toán OR có tính chất giao hoán và kết hợp: ~x | y = y | x~ và ~x | (y | z) = (x | y) | z~.

Để ôn tập nội dung đã học, thầy giáo ra cho cả lớp bài tập về nhà như sau: Cho ~n~ số nguyên không âm ~a_1, a_2, \dotsc, a_n~ và ba số nguyên ~k, L, R~. Hãy đếm xem có bao nhiêu bộ ~k~ chỉ số ~(i_1, i_2, \dotsc, i_k)~ thỏa mãn đồng thời hai điều kiện:

• ~1 \le i_1 < i_2 < \dotsc < i_k \le n~.
• Đặt ~v = a_{i_1} | a_{i_2} | \dotsc | a_{i_k}~ thì ~L \le v \le R~ và ~v~ chia hết cho 3.

Gọi ~S~ là đáp số đúng cho bài tập thầy giáo ra, vì ~S~ có thể có giá trị rất lớn và để học sinh tập trung vào vấn đề chính của bài toán nên thầy giáo chỉ yêu cầu học sinh đưa ra được phần dư của ~S~ khi chia cho ~10^9 + 7~.

Yêu cầu: Hãy giúp Nam xác định phần dư của ~S~ khi chia cho ~10^9 + 7~.

Dữ liệu

Vào từ đầu vào chuẩn (không phải file OR.INP):

• Dòng đầu tiên chứa bốn số nguyên ~n, k, L, R (1 \le k \le n \le 10^6; 0 \le L \le R \le 10^6)~;
• Dòng tiếp theo chứa ~n~ số nguyên không âm ~a_1, a_2, \cdots, a_n~ ~(a_i \le 10^6)~.

Các số trên cùng một dòng cách nhau bởi dấu cách.

Kết quả

Ghi ra đầu ra chuẩn (không phải file OR.OUT) một số nguyên duy nhât là phần dư của ~S~ khi chia cho ~10^9+7~.

Ràng buộc

• Có ~20\%~ số test ứng với ~20\%~ số điểm của bài thỏa mãn ~n \le 20~ và ~a_i \le 200 (1 \le i \le n)~;
• Có ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thỏa mãn ~n \le 200~ và ~a_i \le 200 (1 \le i \le n)~;
• Có ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thỏa mãn ~L = R~ và ~a_i(1 \le i \le n)~ là lũy thừa của 2;
• Có ~20\%~ số test khác ứng với ~20\%~ số điểm của bài thỏa mãn ~L = R~ ;
• Có ~20\%~ số test còn lại ứng với ~20\%~ số điểm của bài không có ràng buộc gì thêm.

Ví dụ

Input

5 2 1 7
1 2 5 6 4

Output

4

Giải thích

Có tất cả 4 cách chọn 2 số trong 5 số thỏa mãn yêu cầu:

1. ~a_1 | a_2 = 1 | 2 = 3~
2. ~a_2 | a_4 = 2 | 6 = 6~
3. ~a_2 | a_5 = 2 | 4 = 6~
4. ~a_4 | a_5 = 6 | 4 = 6~