Kỳ thi Học sinh giỏi Quốc gia 2020 - Ngày 1
Điểm: 7
Đọc đề gốc tại đây.
Alice vừa đoạt giải quán quân trong một kỳ thi lập trình danh giá. Ban tổ chức trao thưởng thông qua một trò chơi như sau. Có ~n~ thẻ xếp trên một hàng dài, trên mỗi thẻ viết một số nguyên dương. Ban tổ chức cho phép Alice thực hiện nhiều bước để chọn ra đúng ~k~ cặp thẻ, mỗi bước thực hiện theo một trong các quy tắc sau:
- Chọn ~2~ thẻ đầu hàng;
- Chọn ~2~ thẻ cuối hàng;
- Chọn ~1~ thẻ đầu hàng và ~1~ thẻ cuối hàng;
- Loại ~1~ thẻ đầu hàng ra khỏi hàng;
- Loại ~1~ thẻ cuối hàng ra khỏi hàng.
Sau mỗi bước nếu chọn được ~2~ thẻ thì loại ~2~ thẻ đó ra khỏi hàng và Alice nhận được số tiền thưởng bằng giá trị tuyệt đối của hiệu hai số ghi trên hai thẻ đó.
Yêu cầu: Hãy giúp Alice tìm cách chơi chọn đúng ~k~ cặp thẻ để đạt được tổng số tiền thưởng là lớn nhất.
Input
- Dòng thứ nhất chứa hai số nguyên dương ~n~ và ~k~ ~(2 \times k \leq n)~;
- Dòng thứ hai chứa ~n~ số nguyên dương là giá trị ghi trên từng thẻ, mỗi thẻ một số tương ứng lần lượt từ đầu hàng. Các số có giá trị không vượt quá ~10^9~.
Các số trên cùng một dòng cách nhau bởi dấu cách.
Output
Ghi ra một số nguyên duy nhất là tổng tiền thưởng lớn nhất tìm được.
Giới hạn
- Có ~40\%~ số test ứng với ~40\%~ số điểm của bài thỏa mãn điều kiện: ~n \leq 300~, ~k \leq 2~;
- ~40\%~ số test khác ứng với ~40\%~ số điểm của bài thỏa mãn điều kiện: ~n \leq 30~, ~2 \times k = n~;
- ~20\%~ số test còn lại ứng với ~20\%~ số điểm của bài thỏa mãn điều kiện: ~n \leq 300~.
Sample Input
6 2
1 3 10 2 1 4
Sample Output
12
Note
Giải thích test ví dụ
- Bước ~1~: Alice chọn hai thẻ cuối hàng là ~1~ và ~4~ và nhận được số tiền thưởng là ~|4 - 1| = 3~;
- Bước ~2~: Alice loại thẻ cuối hàng có giá trị ~2~;
- Bước ~3~: Alice chọn một thẻ đầu hàng và một thẻ cuối hàng là ~1~ và ~10~ và nhận được số tiền thưởng là ~|10 - 1| = 9~;
Tổng tiền thưởng Alice nhận được là ~3 + 9 = 12~.
Điểm: 7
Đọc đề gốc tại đây.
Xe buýt là một phương tiện giao thông phổ biến tại thành phố mà Alice sinh sống bởi tính tiện dụng và giá cả hợp lý của nó. Thành phố có ~n~ bến xe buýt được đánh số từ ~1~ tới ~n~ và có ~m~ tuyến xe buýt hai chiều, mỗi tuyến đang được điều hành bởi một trong hai công ty vận tải ~A~ hoặc ~B~. Cụ thể, tuyến thứ ~i~ ~(1 \leq i \leq m)~ di chuyển giữa hai bến ~u_i~ và ~v_i~ với giá vé do công ty quản lý quy định là ~w_i~.
Lưu ý là giữa hai bến có thể có nhiều hơn một tuyến xe buýt.
Hai công ty ~A~ và ~B~ đều có chính sách giảm giá vé cho những ai thường xuyên đi bằng xe buýt. Cụ thể, mỗi ngày công ty ~A~ sẽ chỉ thu số tiền bằng với giá vé lớn nhất trong tất cả các tuyến được điều hành bởi công ty ~A~ mà khách hàng đã đi trong ngày. Để cạnh tranh, công ty ~B~ cũng có chính sách tương tự: khách hàng sẽ chỉ phải trả số tiền bằng giá vé lớn nhất trong tất cả các tuyến thuộc công ty ~B~ mà người đó đã đi trong ngày.
Nhà Alice ở gần bến xe buýt ~s~ và nơi làm của Alice ở gần bến xe buýt ~t~ nên hàng ngày Alice đều phải đi lại giữa hai bến này thông qua các tuyến xe buýt.
Yêu cầu: Bạn hãy giúp Alice xác định số tiền nhỏ nhất cần bỏ ra mỗi ngày để đảm bảo việc đi từ bến xe buýt ~s~ đến bến xe buýt ~t~.
Input
- Dòng đầu tiên chứa bốn số nguyên dương ~n~, ~m~, ~s~ và ~t~ ~(n, m \leq 50\,000; \; s, t \leq n; \; s \neq t )~;
- Dòng thứ ~i~ ~(1 \leq i \leq m)~ trong ~m~ dòng tiếp theo chứa bốn số nguyên dương ~c_i, u_i, v_i, w_i~ ~(u_i, v_i \leq n; \; u_i \neq v_i; \; w_i \leq 10^9)~ mô tả tuyến xe buýt thứ ~i~ trong đó ~c_i = 1~ nếu tuyến này được điều hành bởi công ty ~A~ hoặc ~c_i = 2~ nếu tuyến này được điều hành bởi công ty ~B~.
Các số trên cùng một dòng cách nhau bởi dấu cách. Dữ liệu đảm bảo luôn tồn tại cách đi lại giữa hai bến xe buýt ~s~ và ~t~ thông qua ~m~ tuyến xe.
Output
Ghi ra một số nguyên duy nhất là số tiền nhỏ nhất cần bỏ ra mỗi ngày để đảm bảo được việc đi từ bến xe buýt ~s~ đến bến xe buýt ~t~ cho Alice.
Giới hạn
- Có ~20\%~ số lượng test ứng với ~20\%~ số điểm của bài thỏa mãn điều kiện: tất cả ~m~ tuyến xe buýt đều được điều hành bởi công ty ~A~;
- ~30\%~ số lượng test khác ứng với ~30\%~ số điểm của bài thỏa mãn điều kiện: ~n, m \leq 5\,000~;
- ~20\%~ số lượng test khác ứng với ~20\%~ số điểm của bài thỏa mãn điều kiện: tồn tại cách đi xe buýt tối ưu trong đó Alice chỉ sử dụng tối đa một tuyến xe của công ty ~B~;
- ~30\%~ số lượng test còn lại ứng với ~30\%~ số điểm của bài không có điều kiện gì thêm.
Sample Input
6 7 1 4
1 1 2 4
2 2 3 7
1 3 4 6
2 1 6 5
1 6 5 5
2 5 4 8
2 2 5 2
Sample Output
12
Note
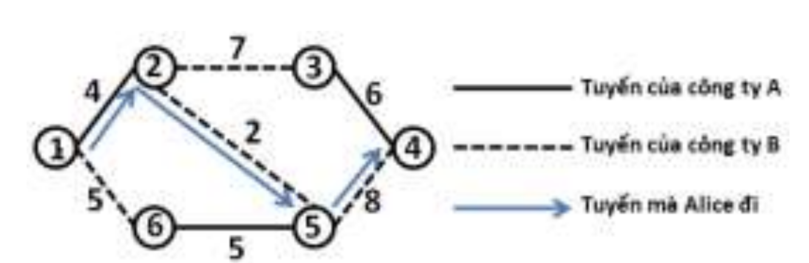
Để đi từ ~1~ đến ~4~, Alice sẽ lần lượt đi tuyến ~(1~, ~2)~ của công ty ~A~ và hai tuyến ~(2~, ~5)~, ~(5~, ~4)~ của công ty ~B~. Khi đó số tiền mà Alice phải trả cho công ty ~A~ là ~4~ và trả cho công ty ~B~ là ~8~.
Điểm: 6
Đọc đề gốc tại đây.
Sau nhiều ngày quan sát các ngôi sao trên bầu trời, Alice nhận thấy có ~n~ chòm sao. Mỗi chòm sao bao gồm một số lượng chẵn các ngôi sao có quy luật vận động giống nhau. Để thuận lợi cho việc theo dõi và khảo sát, Alice đánh số các chòm sao từ ~1~ đến ~n~. Trong mỗi chòm sao đó, các ngôi sao được đánh thứ tự từ ~1~ cho đến số lượng ngôi sao có trong chòm sao. Alice xem xét các ngôi sao trên một hệ trục tọa độ Đề-các, trong đó ngôi sao thứ ~i~ trong chòm sao thứ ~s~ có tọa độ nguyên ~(x_i^s, y_i^s)~. Sau khi phân tích về mặt hình học, Alice phát hiện ra các đặc tính sau:
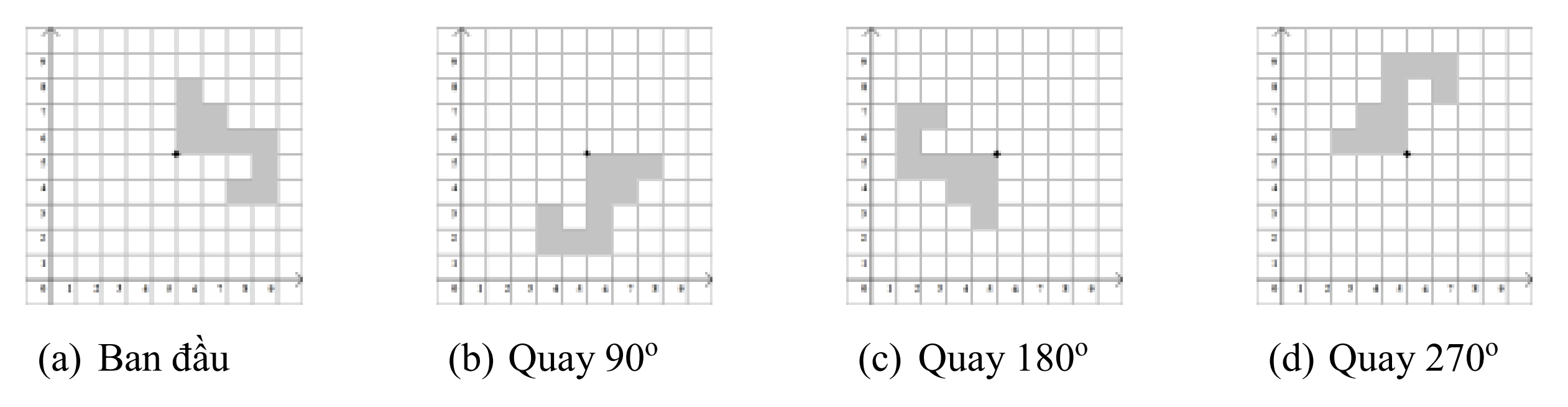
- Trong mỗi chòm sao có duy nhất một ngôi sao không di chuyển, ngôi sao này được đánh số thứ tự ~1~ trong chòm sao đó. Tất cả các ngôi sao còn lại, sau mỗi ngày, mỗi ngôi sao sẽ di chuyển đến một vị trí mới bằng cách thực hiện cùng một góc quay khi lấy ngôi sao được đánh số thứ tự ~1~ làm tâm. Góc quay của mỗi chòm sao là một trong ~3~ loại ~90^o, 180^o, 270^o~ theo chiều kim đồng hồ;
- Tại bất kỳ ngày nào, luôn tồn tại cách vẽ, nối vị trí của tất cả các ngôi sao của mỗi chòm sao thành một đa giác chuẩn không tự cắt, có số đỉnh bằng số ngôi sao trong chòm sao và các đỉnh của đa giác là vị trí của các ngôi sao. Đa giác chuẩn không tự cắt là đa giác có các cạnh song song với trục tọa độ, không có ~3~ đỉnh nào liên tiếp thẳng hàng và không có ~2~ cạnh không liên tiếp nào của đa giác có điểm chung.
Để khảo sát độ phân tán của các chòm sao, sau mỗi ngày, với vị trí mới của các ngôi sao trong mỗi chòm sao, Alice sẽ vẽ một đa giác chuẩn không tự cắt cho từng chòm sao để diện tích được phủ bởi tất cả ~n~ đa giác trên hệ trục tọa độ là lớn nhất.
Yêu cầu: Cho tọa độ các ngôi sao của mỗi chòm sao tại ngày đầu tiên (ngày ~0)~ mà Alice tiến hành quan sát cùng với quy luật quay của từng chòm sao. Hãy tính diện tích phủ lớn nhất bởi ~n~ đa giác được vẽ ở ngày thứ ~d~.
Input
Dòng đầu tiên chứa số nguyên dương ~n~ và số tự nhiên ~d~;
Tiếp theo là ~n~ nhóm dòng, mỗi nhóm mô tả về một chòm sao. Nhóm dòng thứ ~s~ ~(1 \leq s \leq n)~ có khuôn dạng như sau:
- Dòng đầu chứa hai số ~g_s~ và ~r_s~, trong đó ~g_s~ là số ngôi sao trong chòm sao (~g_s~ là số chẵn thỏa mãn ~4 \leq g_s \leq 100)~ và ~r_s~ là giá trị góc quay (một trong ~3~ loại giá trị ~90, 180, 270~);
- Dòng thứ ~i~ trong ~g_s~ dòng tiếp theo chứa hai số nguyên ~x_i^s, y_i^s~ ~(|xi^s|, |y_i^s| \leq 10^6)~. Các ngôi sao trong cùng một chòm sao có tọa độ phân biệt.
Các số trên cùng một dòng cách nhau bởi dấu cách.
Output
Ghi ra một số nguyên duy nhất là diện tích phủ lớn nhất bởi ~n~ đa giác chuẩn được vẽ ở ngày thứ ~d~.
Giới hạn
- Có ~25\%~ số test ứng với ~25\%~ số điểm của bài thỏa mãn điều kiện: ~n \leq 1000~, ~d = 0~ và các ~g_s~ đều có giá trị bằng ~4~;
- ~25\%~ số test khác ứng với ~25\%~ số điểm của bài thỏa mãn điều kiện: ~n \leq 1000~, ~d \leq 10^6~ và các ~g_s~ đều có giá trị bằng ~4~;
- ~25\%~ số test khác ứng với ~25\%~ số điểm của bài thỏa mãn điều kiện: ~n = 2~, ~d \leq 10^6~;
- ~25\%~ số test còn lại ứng với ~25\%~ số điểm của bài thỏa mãn điều kiện: ~n \leq 1000~, ~d \leq 10^6~
Sample Input
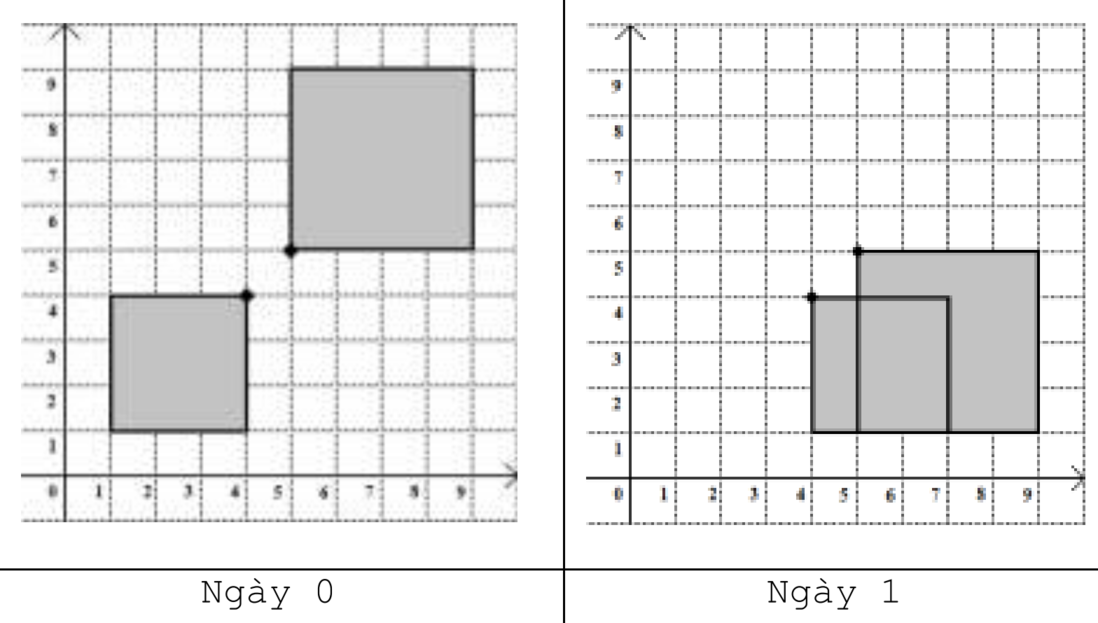
2 1
4 270
4 4
1 4
1 1
4 1
4 90
5 5
9 5
5 9
9 9
Sample Output
19
Note