Trong quá luyện tập cho cuộc thi học sinh giỏi sắp tới, Hùng được thầy giáo giao cho thử sức giải bài toán nén xâu kí tự (chỉ gồm các kí tự la tinh in hoa) sau đây.

Phép cộng trên hai xâu ~x~ và ~y~, kí hiệu là ~x + y~, được hiểu là ghép xâu ~y~ liền sau xâu ~x~. Xuất phát từ hai xâu ~u,\,v~ và số nguyên ~k~, xâu ~F_k~ được tạo theo luật sau (còn được gọi là luật tựa Fibonacci):

Ví dụ, với hai xâu ~u =~ AB, ~v =~ C và ~k = 5~ ta có:

Giả sử xâu ~T~ có độ đài ~n~ là xâu được tao theo luật trên từ hai xâu xuất phát ~u_T,\,v_T~ có độ dài tương ứng là ~n_1,\,n_2~. Như vậy, ~v_T~ là xâu gồm ~n_2~ kí tự đầu tiên của xâu ~T~ và ~u_T~ là xâu gồm ~n_1~ kí tự tiếp theo của xâu ~T~. Xâu ~T~ có thể được nén thành bộ ~(u_T,\,v_T,\,n)~ vì từ 3 thông tin ~u_T,\,v_T~ và ~n~ ta có thể khôi phục được xâu ~T~ theo luật trên. Ví dụ xâu ~T =~ CABCCAB có thể được nén thành bộ ~(~AB, C, ~7)~.

Một xâu ~S~ bất kì có độ dài ~m~ cũng có thể được nén theo cách như trên. Với hai số nguyên dương ~m_1,\,m_2\,(m_1 + m_2 \le m)~, gọi ~v_S~ là xâu gồm ~m_2~ kí tự đầu tiên của xâu ~S~ và ~u_S~ là xâu gồm ~m_1~ kí tự tiếp theo trên xâu ~S~. Khi đó, xâu ~S~ có thể được nén thành bộ ~(u_S,\,v_S,\,m)~. Tuy nhiên, từ 3 thông tin ~u_S,\,v_S~ và ~m~ ta có thể không khôi phục được chính xác xâu ~S~. Do đó, người ta đánh giá độ lỗi của phương pháp nén xâu này như sau. Với bộ ~(u_S,\,v_S,\,m)~, tạo xâu ~F_k~ với k nhỏ nhất mà độ dài ~F_k~ lớn hơn hoặc bằng ~m~ theo luật tựa Fibonacci từ hai xâu xuất phát ~F_1 = u_S~, ~F_2 = v_S~. Độ lỗi của việc nén xâu ~S~ được tính bằng số lượng vị trí ~i~ mà ~S[i]~ khác với ~F_k[i]~, trong đó ~S[i]~ và ~F_k[i]~ tương ứng là kí tự thứ ~i~ của xâu ~S~ và xâu ~F_k~ với ~i \le m~.

Ví dụ, với ~m_1 = 2~ và ~m_2 = 1~, xâu ~S =~ CABACC có độ dài ~m = 6~ được nén thành bộ ~(~AB, C, ~6)~, sau đó tạo ra xâu ~F_5 =~ CABCCAB. Khi đó đội lỗi của việc nén xâu ~S~ là ~2~ do có hai kí tự ở các vị trí thứ 4 và thứ 6 của ~S~ và ~F_5~ là khác nhau.

Nhận thấy rằng ~m_2 + m_1~ kí tự đầu tiên của xâu ~S~ ảnh hưởng rất lớn đến độ lỗi của việc nén xâu. Vì vậy, người ta tiến hành thay đổi không quá ~r~ kí tự trong ~m_2 + m_1~ kí tự đầu tiên của xâu ~S~ để biến xâu ~S~ thành xâu ~S^*~ sao cho độ lỗi của việc nén xâu ~S^*~ là nhỏ nhất. Việc thay đổi một kí tự là thay kí tự đó bởi một kí tự khác.

Yêu cầu: Cho các số nguyên ~m,\,m_1,\,m_2,\,r~ và xâu ~S~, hãy tìm cách thay đổi không quá ~r~ kí tự trong ~m_2 + m_1~ kí tự đầu tiên của xâu ~S~ để biến xâu ~S~ thành xâu ~S^*~ sao cho độ lỗi của việc nén xâu ~S^*~ là nhỏ nhất.

Lưu ý: Đọc input, output từ stdin/stdout (không phải từ file như trong đề)

Dữ liệu

Dòng thứ nhất chứa bốn số nguyên cách nhau bởi dấu cách ~m,\,m_1,\,m_2,\,r\,(0 \le r \le m_2 + m_1 \le m)~; Dòng thứ hai chứa xâu ~S~ độ dài ~m~, xâu chỉ gồm các kí tự thuộc tập kí tự chữ cái la tinh in hoa (từ A đến Z).

Kết quả

Ghi ra một số nguyên là độ lỗi nhỏ nhất tìm được.

Ràng buộc

• Có ~30\%~ số test tương ứng ~30\%~ số điểm của bài thỏa mãn điều kiện: ~r = 0;\,m \le 10^3;~
• ~40\%~ số test khác ứng với ~40\%~ số điểm của bài thỏa mãn điều kiện: ~r = m_1 + m_2 \le 10;\,m \le 10^3~ và xâu ~S~ chỉ gồm hai kí tự A và B~;~
• ~30\%~ số test còn lại ứng với ~30\%~ số điểm của bài thỏa mãn điều kiện: ~m \le 10^5~.

Sample Input

6 2 1 1
CABAAC

Sample Output

1

Giải thích

Trong ví dụ trên, cách thay đổi tối ưu nhất là thay kí tự đầu tiên của xâu ~S~ thành A để nhận được xâu ~S^*~ = AABAAC. Với ~m_1 = 2~ và ~m_2 = 1~, xâu ~S^*~ được nén thành bộ ~(~AB, A, ~6)~, ta tạo ra xâu ~F_5~ = AABAAAB. Khi đó, độ lỗi của việc nén xâu ~S^*~ bằng ~1~ do kí tự ở vị trí thứ 6 của ~S^*~ và ~F_5~ là khác nhau.

Công ty LDK đang sản xuất robot vận chuyển hàng hóa tự động trên mặt phẳng. Để làm việc đó, công ty tiến hành huấn luyện các robot trên một địa hình phẳng được chia thành một lưới các ô vuông gồm ~3~ dòng (đánh số từ ~1~ đến ~3~ theo chiều từ trên xuống dưới) và ~n~ cột (đánh số từ ~1~ đến ~n~ theo chiều từ trái sang phải). Ô giao giữa dòng ~i~, cột ~j~ được gọi là ô ~(i, j)~ và thuộc một trong 5 loại dưới đây:

Ví dụ một địa hình kích thước ~3 \times 6~.

~1)~ Ô xuất phát, kí hiệu là S~;~
~2)~ Ô kết thúc, kí hiệu là T~;~
~3)~ Ô trống, kí hiệu là .~;~
~4)~ Ô cấm, kí hiệu là #~;~
~5)~ Ô kém chất lượng, kí hiệu là *~.~

Một đường thử nghiệm cho robot là một dãy liên tiếp các ô chung cạnh, bắt đầu tại ô S, kết thúc tại một ô T và thỏa mãn các điều kiện sau:

• Không chứa ô cấm~;~
• Không chứa ô S, T nào khác~;~
• Số ô kém chất lượng không quá một ô.

Yêu cầu: Cho biết thông tin các ô của lưới, hãy giúp công ty tìm phương án thiết kế có nhiều đường thử nghiệm nhất mà mỗi ô của lưới thuộc không quá một đường thử nghiệm.

Lưu ý: Đọc input, output từ stdin/stdout (không phải từ file như trong đề)

Dữ liệu

Dòng thứ nhất chứa một số nguyên ~n;~

Dòng thứ ~i~ trong số ~3~ tiếp theo chứa xâu mô tả thông tin các ô liên tiếp trên hàng thứ ~i~ của lưới.

Kết quả

Ghi ra một số nguyên là số đường thử nghiệm nhiều nhất tìm được.

Ràng buộc

• Có ~30\%~ số test ứng với ~30\%~ số điểm của bài thỏa mãn điều kiện: ~n \le 100~, không có ô kém chất lượng và các ô thuộc hàng ~2~ và hàng ~3~ của địa hình đều là ô cấm~;~
• ~30\%~ số test khác ứng với ~30\%~ số điểm của bài thỏa mãn điều kiện: ~n \le 100~ và địa hình không có ô kém chất lượng~;~
• ~30\%~ số test khác ứng với ~30\%~ số điểm của bài thỏa mãn điều kiện: ~n \le 10^5~ và các ô thuộc hàng 3 của địa hình đều là ô cấm~;~
• ~10\%~ số test còn lại ứng với ~10\%~ số điểm của bài thỏa mãn điều kiện: ~n \le 10^5~ và không có điều kiện gì thêm trên địa hình.

Sample Input

10
T.*S..##S#
**###T#T.S
.*S.*.##T#

Sample Output

3

Ông Hàm là chủ một trang trại nuôi bò có dạng hình đa giác lồi ~N~ đỉnh. Cổng của trang trại là một cạnh của đa giác, kí hiệu là ~(a, b)~, với ~a,\,b~ là hai đỉnh của đa giác. Mùa đông lạnh giá đang tới, ông xây dựng hệ thống sưởi cho đàn bò của mình như sau.

Đầu tiên ông đặt tại mỗi đỉnh đa giác một cột đèn sưởi, dây điện nối liên thông giữa một số cột đèn với nhau. Vì lý do an toàn nên ông thiết kế dây điện chỉ chạy trên các đoạn thẳng men theo các cạnh của đa giác mà không đi vào bên trong trang trại và không chạy ngang qua cạnh ~(a, b)~. Ông đặt hai cầu dao tổng tại hai đỉnh ~a,\, b~ nhằm đưa nguồn điện từ bên ngoài vào hệ thống đèn sưởi bắt đầu từ ~a,\,b~. Để tiết kiệm chi phí, ngoài cạnh ~(a, b)~ ông không cho chạy dây qua một cạnh dài nhất trong số các cạnh còn lại của đa giác. Sau khi hoàn thành ông tính ra tổng độ dài dây điện sử dụng là khá lớn, nên ông quyết định tiết kiệm tối đa dây điện sử dụng trong việc dẫn nguồn điện vào.

Nhằm đảm bảo nguồn điện liên tục cho hệ thống đèn sưởi của trang trại, ông chủ trang trại tìm cách đi dây sao cho tất cả đèn sưởi đều có hai nguồn điện đi tới. Trong trường hợp có một nguồn điện bị mất thì vẫn còn một nguồn điện dự phòng cung cấp. Ông quyết định phương án đi dây điện ngầm từ hai nguồn điện đến hai đỉnh ~a,\,b~, ký hiệu vị trí hai nguồn điện đó là ~c~ và ~d~. Lưu ý rằng dây điện không nhất thiết phải chạy riêng rẽ trực tiếp từ từng nguồn điện đến hai đỉnh ~a,\,b~ mà có thể đi chung và rẽ nhánh ở một số điểm trên đường đi, nhưng phải đảm bảo mỗi đỉnh ~a,\,b~ đều có cách dẫn điện từ cả hai nguồn ~c,\,d~ theo hệ thống dây điện mới thiết kế. Do đường điện đi ngầm nên các dây điện có thể chạy bên trong trang trại hoặc trên cạnh ~(a, b)~. Ngoài ra ông còn phát hiện ra bốn điểm ~a,\,b,\,c,\,d~ có vị trí liên hệ đặc biệt với nhau (được mô tả chi tiết trong phần ràng buộc của bài toán).

Hình vẽ dưới đây minh họa một cách đi dây điện. Đa giác biểu diễn trang trại bao gồm các đỉnh ~a,\,g,\,b,\,f,\,h~ với ~(a, b)~ là cổng và ~(g, h)~ là cạnh dài nhất khác cạnh ~(a, b)~ nên không được nối. Các đoạn nét liền mô tả đi dây dọc theo các cạnh của đa giác. Các đoạn nét đứt mô tả việc đi dây từ hai nguồn ~c,\,d~ tới hai đỉnh ~a,\,b~. Bốn điểm ~a,\,b,\,c,\,d~ tạo thành một hình vuông và ~e~ là điểm rẽ nhánh. Tổng độ dài lượng dây điện sử dụng trong hình vẽ bằng tổng độ dài các đoạn:

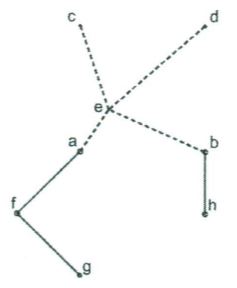
Yêu cầu: Biết tọa độ vị trí các đỉnh của đa giác và tọa độ vị trí của hai nguồn điện, hãy giúp ông Hàm thiết kế đi dây điện sao cho tổng độ dài dây điện sử dụng là ít nhất. Độ dài dây điện được tính bằng tổng độ dài đoạn đường mà dây đi qua, quanh các cạnh của đa giác và từ hai nguồn điện đến ~a,\,b~.

Lưu ý: Đọc input, output từ stdin/stdout (không phải từ file như trong đề)

Dữ liệu

• Dòng thứ nhất chứa một số nguyên ~N~ là số đỉnh của đa giác~;~
• Dòng thứ hai chứa hai số nguyên ~x_a,\,y_a~ là tọa độ của đỉnh ~a;~
• Dòng thứ ba chứa hai số nguyên ~x_b,\,y_b~, là tọa độ của đỉnh ~b;~
• Mỗi dòng trong số ~N – 2~ dòng tiếp chứa hai số nguyên ~x,\,y~ là tọa độ một trong số ~N – 2~ đỉnh còn lại của đa giác.
• Dòng cuối cùng chứa bốn số nguyên ~x_c,\,y_c,\,x_d,\,y_d~ là các tọa độ tương ứng của vị trí hai nguồn điện ~c~ và ~d~.

Lưu ý: Trong dữ liệu vào, các đỉnh của đa giác không nhất thiết được liệt kê theo một thứ tự nhất định cho trước. Dữ liệu đảm bảo không có ba đình nào của đa giác thẳng hàng. Tất cả tọa độ cho trong dữ liệu vào nằm trong khoảng ~[-10^8, 10^8]~. Các số trên cùng một dòng cách nhau bởi một dấu cách

Kết quả

Ghi ra một số duy nhất là độ dài dây điện tìm được. Số in ra cần làm tròn đến ~2~ chữ số sau dấu phẩy động.

Ràng buộc

• Có ~30\%~ số lượng test ứng với ~30\%~ số điểm của bài thỏa mãn điều kiện: ~3 \le N \le 100~, các tọa độ đỉnh của đa giác được liệt kê xuôi chiều kim đồng hồ theo trình tự xuất hiện trong file dữ liệu vào, và bốn vị trí ~a,\,b,\,c,\,d~ cùng nằm trên một đường thẳng~;~
• ~30\%~ số lượng test khác ứng với ~30\%~ số điểm của bài thỏa mãn điều kiện: ~3 \le N \le 10~, các tọa độ của ~a,\,b,\,c,\,d~ nằm trong khoảng ~[-5, 5]~, và đường thẳng đi qua hai điểm ~c,\,d~ là đường trung trực của đoạn thẳng ~[a, b]~, đồng thời ~c,\,d~ thuộc cùng một nửa mặt phẳng tạo bởi đường thẳng đi qua ~a,\,b;~
• ~20\%~ số lượng test khác ứng với ~20\%~ số điểm của bài thỏa mãn điều kiện: ~3 \le N \le 100~, và đường thẳng đi qua hai điểm ~c,\,d~ là đường trung trực của đoạn thẳng ~[a, b]~, đồng thời ~c,\,d~ thuộc cùng một nửa mặt phẳng tạo bởi đường thẳng đi qua ~a,\,b;~
• ~20\%~ số lượng test còn lại ứng với ~20\%~ số điểm của bài thỏa mãn điều kiện: ~3 \le N \le 100~, và bốn đỉnh ~a,\,b,\,c,\,d~ tạo thành một hình vuông.

Sample Input

4
4 0
0 0
0 4
4 4
-1 0 5 0

Sample Output

14.00

Giải thích

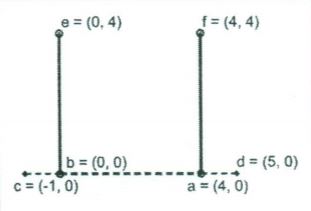
Trong ví dụ trên, các đoạn dây điện nối dọc theo các cạnh của đa giác bao gồm: ~a~ nối với ~f~ và ~b~ nối với ~e~. Ngoài cạnh ~(a, b)~, một cạnh dài nhất không được nối dây là cạnh ~(e, f)~. Cách kết nối từ vị trí hai nguồn điện ~c~ và ~d~ tới ~a~ và ~b~ sử dụng ít dây điện nhất là nối ~a~ với ~d~, nối ~a~ với ~b~, và nối ~b~ với ~c~.