Đối với nhiều người, đại học là bước đánh dấu giai đoạn trưởng thành bắt đầu. Nếu như mái trường cấp ba luôn đem đến những ngày hồn nhiên, mơ mộng cùng biết kỉ niệm êm đềm, yên vui; mái trường đại học lại cho ta những góc xù xì, thô ráp của cuộc sống. Thời cấp ba, ta yên tâm sống trong vỏ bọc của gia đình, tha hồ đắm say trong bạn bè, bài vở và thầy cô. Còn khi tuổi 18 sang, ta thoát ra khỏi cái kén kia và tự mình đối mặt với những chông chênh của cuộc sống. Bởi thế, kể từ khi lên đại học, ta cần tự xây dựng chương trình học cho chính mình, còn nhà trường và thầy cô chỉ là những người tư vấn...

Ở một trường đại học nọ, nhà trường tổ chức giảng dạy ~n~ môn học. Các môn học được đánh số từ ~1~ đến ~n~. Để hoàn thành chương trình học, sinh viên không bắt buộc phải học hết cả ~n~ môn này. Sinh viên có thể đăng kí học hay bỏ bất kì môn nào, nhưng hoàn thành càng nhiều môn thì bằng tốt nghiệp sẽ càng ấn tượng. Chỉ có một ràng buộc duy nhất: Sinh viên phải học các môn theo thứ tự chỉ số tăng dần. Cụ thể, nếu một sinh viên đã quyết định sẽ học cả hai môn ~i~ và ~j~ với ~i < j~, bạn này sẽ phải học xong môn ~i~ trước khi bắt đầu học môn ~j~.

Là cố vấn học tập lâu năm, GS. PVH được nghe nhiều từ sinh viên về trải nghiệm khi học các môn ở trường. Từ đó, GS. PVH đánh giá rằng độ hấp dẫn của môn học thứ ~i~ là ~e_i~. Độ hấp dẫn của một môn học có thể là dương hoặc âm: có những môn khiến sinh viên tràn ngập niềm tin yêu vào cuộc sống (ví dụ như Triết học, Lịch sử Đảng hay Tư tưởng Hồ Chí Minh), nhưng cũng có nhiều môn khá "khoai" khiến nhiều sinh viên thấy áp lực và có phần nghẹt thở. Mỗi sinh viên sẽ có một chỉ số để đo "cảm hứng học tập" trong suốt 5 năm học tại trường. Khi học xong một môn nào, cảm hứng học tập của sinh viên sẽ tăng lên một lượng bằng độ hấp dẫn của môn đó. GS. PVH biết rằng, nếu cảm hứng học tập của một sinh viên xuống dưới ~0~, sinh viên đó sẽ ngập trong khủng hoảng và có thể dẫn tới trầm cảm, tự kỷ hay những sang chấn tâm lý khác. Vì vậy đây là điều cần tránh bằng mọi giá.

Năm học mới này, GS. PVH được giao làm cố vấn học tập cho ~m~ tân sinh viên. Thông qua cuộc trò chuyện đầu tiên, GS. PVH đánh giá cảm hứng học tập lúc mới vào trường của sinh viên thứ ~j~ là ~s_j~. GS. PVH cần tư vấn cho các sinh viên cách lựa chọn môn học. GS. PVH luôn muốn tất cả đều được học nhiều môn nhất có thể, nhưng cần đảm bảo rằng cảm hứng học tập của bất kì ai không bao giờ rơi xuống dưới ~0~ để ai cũng có một thời sinh viên đáng nhớ.

Do số tân sinh viên năm nay rất lớn, các bạn hãy giúp GS. PVH tính số môn học tối đa mỗi người có thể học nhé.

Input

Dòng đầu tiên chứa hai số nguyên ~n~ và ~m~ ~(1 \leq n \leq 2 \cdot 10^3, 1 \leq m \leq 3 \cdot 10^5)~, lần lượt là số môn học trong trường và số tân sinh viên GS. PVH nhận làm cố vấn.

Dòng thứ hai chứa ~n~ số nguyên ~e_1, e_2, \ldots, e_n~ ~(-10^9 \leq e_i \leq 10^9)~ thể hiện độ hấp dẫn của các môn học trong trường.

Dòng thứ ba chứa ~m~ số nguyên ~s_1, s_2, \ldots, s_m~ ~(0 \leq s_j \leq 2 \cdot 10^{12})~ thể hiện cảm hứng học tập của mỗi tân sinh viên ở thời điểm nhập trường.

Output

In ra ~m~ số nguyên trên một dòng, số thứ ~j~ thể hiện số môn tối đa tân sinh viên thứ ~j~ có thể học sao cho cảm hứng học tập không rơi xuống dưới ~0~ ở bất kì thời điểm nào.

Sắp tát

Bộ test của bài được chia làm các sắp tát như sau:

• Sắp tát ~1~ (~11~ điểm): Dãy ~e~ được sắp xếp tăng dần hoặc giảm dần. Nói cách khác, một trong hai điều sau là đúng: ~e_1 \leq e_2 \leq \ldots e_n~ hoặc ~e_1 \geq e_2 \geq \ldots \geq e_n~.
• Sắp tát ~2~ (~7~ điểm): ~n \leq 20~ và ~m \leq 30~
• Sắp tát ~3~ (~8~ điểm): ~n \leq 20~
• Sắp tát ~4~ (~19~ điểm): ~m \leq 3000~
• Sắp tát ~5~ (~25~ điểm): Không có ràng buộc gì thêm.

Điểm tối đa của bài là ~70~ điểm.

Ví dụ

Input 1

7 3
-3 0 4 -7 -4 -5 4 
2 11 15

Output 1

4 6 7

Input 2

8 4
-2 -2 0 7 1 -9 9 -7
1 1 20 3

Output 2

6 6 8 7

Giải thích

Trong ví dụ đầu tiên:

• Sinh viên thứ nhất chọn học các môn thứ ~2~, ~3~, ~6~, ~7~. Khi đó, cảm hứng học tập của sinh viên lúc nhập trường là ~2~, sau khi học các môn lần lượt là ~2 + 0 = 2~, ~2 + 4 = 6~, ~6 + (-5) = 1~ và ~1 + 4 = 5~. Như vậy, không khi nào cảm hứng học tập của bạn rơi xuống dưới ~0~.
• Sinh viên thứ hai chọn học tất cả các môn, trừ môn thứ ~5~. Khi đó, cảm hứng học tập của sinh viên lúc nhập trường là ~11~, sau khi học các môn lần lượt là ~11 + (-3) = 8~, ~8 + 0 = 8~, ~8 + 4 = 12~, ~12 + (-7) = 5~, ~5 + (-5) = 0~ và ~0 + 4 = 4~.

Chào cờ và hát Quốc ca là một nghi lễ thiêng liêng, nghi thức quan trọng thể hiện tinh thần yêu nước, niềm tự hào, tự tôn dân tộc và trách nhiệm của mỗi công dân đối với đất nước, với nhân dân. Vì lẽ đó, hầu hết các trường phổ thông đều tổ chức lễ chào cờ vào mỗi sáng thứ hai hàng tuần, nhằm giáo dục học sinh về lòng yêu nước và trách nhiệm cống hiến của mỗi công dân với quốc gia, dân tộc.

Một lớp học nọ có ~n~ học sinh, các bạn được đánh số từ ~1~ đến ~n~. Trong lớp học có ~m~ cặp học sinh có "có quan hệ đặc biệt" với nhau. Quan hệ đặc biệt này rất đa dạng, nhưng cũng có thể hết sức đơn giản. Chẳng hạn, nếu bạn ~x~ có quan hệ đặc biệt với bạn ~y~, ~x~ có thể là "thành phố New York" của ~y~, hoặc ~x~ và ~y~ cùng thích một người, ~x~ thích ~y~ nhưng ~y~ đã phũ ~x~. Đó cũng có thể là những mối quan hệ phức tạp hơn, như ~x~ là người yêu mới của người yêu cũ của ~y~, hoặc người yêu cũ của người yêu mới của ~x~ lại là người yêu mới của người yêu cũ của ~y~, vân vân và mây mây. Nhưng dù có thế nào, những cặp quan hệ đặc biệt này cũng là kẻ thù không đội trời chung và chắc chắn một khi có quan hệ đặc biệt thì không bao giờ muốn nhìn mặt nhau cả.

Vào mỗi buổi sáng chào cờ, lớp trưởng được giao nhiệm vụ gọi cả lớp xuống sân. Sau đó, lớp trưởng cần xếp ~n~ bạn thành một hàng thẳng. Lớp trưởng được quyết định vị trí đứng của từng bạn trong hàng, nhưng cô giáo yêu cầu thứ tự xếp hàng ở mỗi buổi phải khác nhau để tránh các bạn thân nhau tụ tập nói chuyện.

Do cả ~n~ bạn đều phải tham gia buổi chào cờ; thứ tự xếp hàng của cả lớp được biểu diễn bởi một dãy ~(p_1, p_2, \ldots, p_n)~ là hoán vị của các số ~(1, 2, \ldots, n)~, trong đó bạn ~p_1~ đứng đầu hàng, bạn ~p_2~ đứng liền sau bạn ~p_1~, ~\ldots~, bạn ~p_n~ đứng cuối hàng.

Lớp trưởng xây dựng phương án xác định vị trí xếp hàng của các bạn như sau:

• Đầu tiên, lớp trưởng liệt kê ra tất cả các hoán vị của các số từ ~1~ đến ~n~.
• Tiếp theo, do những cặp bạn "có quan hệ đặc biệt" ở trên không muốn nhìn mặt nhau, việc để họ đứng cạnh nhau là vô cùng nguy hiểm. Do đó, nếu bạn ~x~ có "quan hệ đặc biệt" với bạn ~y~, lớp trưởng loại bỏ tất cả các hoán vị mà trong đó hai bạn ~x~ và ~y~ đứng cạnh nhau.
• Với các hoán vị còn lại, lớp trưởng sắp xếp chúng theo thứ tự từ điển tăng dần.
• Vào buổi chào cờ thứ ~k~, lớp trưởng sẽ sắp xếp các bạn theo hoán vị thứ ~k~ trong danh sách sau khi sắp xếp.

Do lớp học rất đông, việc liệt kê tất cả các hoán vị là bất khả thi. Vì vậy, các bạn hãy cho lớp trưởng biết, với phương án như trên, trong buổi chào cờ thứ ~k~ các bạn sẽ xếp hàng như thế nào.

Nhắc lại, dãy ~(a_1, a_2, \ldots, a_n)~ được gọi là "có thứ tự từ điển" nhỏ hơn dãy ~(b_1, b_2 \ldots, b_n)~ khi và chỉ khi tồn tại chỉ số ~i~ sao cho ~1 \leq i \leq n~, ~a_i < b_i~ và với mọi ~1 \leq j < i~ ta luôn có ~a_j = b_j~.

Input

Dòng đầu tiên chứa ba số nguyên ~n~, ~m~ và ~k~ ~(1 \leq n \leq 100, 0 \leq m \leq 10, 1 \leq k \leq 4 \cdot 10^{18})~ lần lượt là số bạn trong lớp, số cặp có quan hệ đặc biệt và buổi chào cờ đang xét.

Trong ~m~ dòng còn lại, mỗi dòng chứa hai số nguyên ~x~ và ~y~ ~(1 \leq x, y \leq n, \sin x \cos y \neq \sin y \cos x)~ cho biết hai bạn ~x~ và ~y~ có "quan hệ đặc biệt" với nhau.

Output

In ra ~n~ số nguyên thể hiện thứ tự xếp hàng của các bạn trong buổi chào cờ thứ ~k~. Dữ liệu vào đảm bảo luôn tồn tại đáp án.

Sắp tát

Bộ tét của bài được chia làm các sắp tát như sau:

• Sắp tát ~1~ (~7~ điểm): ~n \leq 10~
• Sắp tát ~2~ (~7~ điểm): ~k \leq 10^5~
• Sắp tát ~3~ (~7~ điểm): ~m = 0~
• Sắp tát ~4~ (~12~ điểm): Trong tất cả các cặp bạn "có quan hệ đặc biệt" ~(x, y)~, ta luôn có ~xy + 1 = x + y~.
• Sắp tát ~5~ (~13~ điểm): ~n \leq 20~
• Sắp tát ~6~ (~24~ điểm): Không có ràng buộc gì thêm.

Điểm tối đa của bài là ~70~ điểm.

Ví dụ

Input 1

4 2 1
1 4
2 3

Output 1

1 2 4 3

Input 2

4 2 2
1 4
2 3

Output 2

1 3 4 2

Input 3

4 2 3
1 4
2 3

Output 3

2 1 3 4

Input 4

4 2 5
1 4
2 3

Output 4

3 1 2 4

Input 5

4 2 8
1 4
2 3

Output 5

4 3 1 2

Ta biết nhau từ lâu rồi

Ta hiểu từng thói quen của nhau

Tuy không phải người yêu với nhau

Ta vẫn hơn là bạn...

Đã bao giờ bạn từng trải qua những mối quan hệ mập mờ chưa, là kiểu "trên tình bạn mà dưới tình yêu" đó? Đó là khi đôi ta đã ở rất gần nhau, luôn cùng nhau đến trường, luôn ngồi cạnh nhau học, luôn quan tâm hỏi han nhau nhưng chẳng ai mở lời nói ba từ ngọt ngào ấy. Đó cũng có thể là khi tối qua anh vừa đi cùng em, trong đêm đông giá lạnh mà lòng ấm áp; ấy thế mà sáng nay em đã đắm say bên ai đó rồi. Hay là khi em vừa tặng anh một món quà dễ thương đầy ẩn ý, rồi lại tươi cười cùng ai kia... Nói chung, "rõ ràng" thì sẽ hoặc là mãi thuộc về nhau hoặc đường tình đôi ta cách xa ngàn dặm; còn "mập mờ" thì lúc gần lúc xa, lúc giao nhau lúc lại chia tách. Ấy mà thôi, "mập mờ" trong tình yêu thì nói cả buổi không hết. Bây giờ mình muốn nói về cái "rõ ràng" và "mập mờ" khác cơ.

Xét hai tập hợp ~A~ và ~B~ bất kì, ta nói hai tập hợp ~A~ và ~B~ có "quan hệ rõ ràng" với nhau khi và chỉ khi ít nhất một trong ba điều sau là đúng:

• ~A~ là tập hợp con của tập hợp ~B~ ~(A \subset B)~.
• ~B~ là tập hợp con của tập hợp ~A~ ~(B \subset A)~.
• ~A~ và ~B~ không có phần tử chung ~(A \cap B = \oslash)~.

Ngược lại, nếu cả ba trường hợp trên đều không xảy ra, ta nói ~A~ và ~B~ có "quan hệ mập mờ" với nhau.

Trong bài tập này, bạn được cho một cây gồm ~n~ đỉnh, với các đỉnh được đánh số từ ~1~ đến ~n~. Bạn cần phải trả lời ~t~ câu hỏi. Trong mỗi câu hỏi, bạn được cho ~q~ cặp đỉnh ~(u_1, v_1), (u_2, v_2), \ldots, (u_q, v_q)~. Với mỗi cặp đỉnh ~(u_i, v_i)~, ta gọi ~P_i~ là tập hợp các đỉnh trên đường đi từ ~u_i~ đến ~v_i~. Bạn cần cho biết trong các tập hợp ~P_1, P_2, \ldots, P_q~ có hai tập hợp nào có "quan hệ mập mờ" với nhau hay không.

Input

Dòng đầu tiên chứa số nguyên ~\theta~ ~(1 \leq \theta \leq 6)~ là số thứ tự của subtask chứa tét này.

Dòng thứ hai chứa số nguyên ~n~ ~(1 \leq n \leq 3 \cdot 10^5)~ là số đỉnh của cây.

Trong ~n - 1~ dòng tiếp theo, mỗi dòng chứa hai số nguyên ~x~ và ~y~ ~(1 \leq x, y \leq n)~ cho biết trên cây có một cạnh nối hai đỉnh ~x~ và ~y~.

Dòng tiếp theo chứa số nguyên ~t~ ~(1 \leq t \leq 10^6)~ là số câu hỏi bạn cần trả lời.

Cuối cùng là ~t~ nhóm dòng mô tả ~t~ câu hỏi. Mỗi nhóm dòng có dạng như sau:

• Dòng đầu tiên chứa số nguyên ~q~ ~(1 \leq q \leq 10^6)~ là số cặp đỉnh.
• Trong ~q~ dòng còn lại, dòng thứ ~i~ chứa hai số nguyên ~u_i~ và ~v_i~ ~(1 \leq u_i, v_i \leq n)~ thể hiện cặp đỉnh thứ ~i~.

Dữ liệu vào đảm bảo tổng giá trị của ~q~ trong các câu hỏi của một tét không quá ~10^6~.

Output

Gồm ~t~ dòng, mỗi dòng chứa câu trả lời cho một câu hỏi: In ra "RO RANG" nếu với mọi cặp chỉ số ~(i, j)~ sao cho ~1 \leq i, j \leq q~, hai tập hợp ~P_i~ và ~P_j~ có "quan hệ rõ ràng" với nhau. Ngược lại, in ra "MAP MO" khi tồn tại một cặp tập hợp ~(P_i, P_j)~ có "quan hệ mập mờ" với nhau.

Sắp tát

Bộ tét của bài được chia làm các sắp tát như sau:

• Sắp tát ~1~ (~6~ điểm): ~n \leq 90~ và ~\sum q \leq 2000~
• Sắp tát ~2~ (~8~ điểm): ~n \leq 4000~ và ~\sum q \leq 2000~
• Sắp tát ~3~ (~10~ điểm): ~\sum q \leq 5000~
• Sắp tát ~4~ (~12~ điểm): Cây có dạng đường thẳng.
• Sắp tát ~5~ (~9~ điểm): Cây có dạng cây nhị phân đầy đủ.
• Sắp tát ~6~ (~15~ điểm): Không có ràng buộc gì thêm.

Điểm tối đa của bài là ~60~ điểm.

Ví dụ

Input 1

1
9 
1 2
2 3
2 4
3 5
4 6
2 7
7 8
7 9
2
4
1 1
5 6
3 4
8 9
2
1 7
5 6

Output 1

RO RANG
MAP MO

Giải thích

Hình vẽ dưới đây mô tả cây trong ví dụ trên:

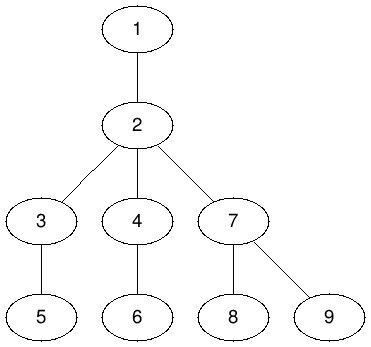
Trong câu hỏi thứ nhất, ta có:

• ~P_1 = \{1\}~
• ~P_2 = \{5, 3, 2, 4, 6\}~
• ~P_3 = \{3, 2, 4\}~
• ~P_4 = \{8, 7, 9\}~

Tất cả các tập hợp trên đều có "quan hệ rõ ràng" với các tập hợp khác.

Trong câu hỏi thứ hai, ta có ~P_1 = \{1, 2, 7\}~ và ~P_2 = \{5, 3, 2, 4, 6\}~. Hai tập hợp này có "quan hệ mập mờ" với nhau.