Thành phố Nồi Hạ có phân bổ dân cư hết sức đặc biệt: Thành phố có ~r \cdot c~ khu dân cư đựoc xếp dưới dạng lưới hình chữ nhật gồm ~r~ hàng và ~c~ cột. Các hàng được đánh số từ ~1~ đến ~r~, các cột được đánh số từ ~1~ đến ~c~. Khu dân cư nằm trên giao của hàng ~i~ và cột ~j~ được kí hiệu là ~(i, j)~.

Trong đợt khảo sát vừa qua, lãnh đạo thành phố đã đi từng ngõ, gõ từng nhà để thu thập thông tin về chất lượng cuộc sống ở các khu dân cư. Tiếp đó, họ xếp hạng các khu dân cư bằng các con số phân biệt từ ~1~ đến ~r \cdot c~. Khu dân cư xếp hạng ~1~ có chất lượng cuộc sống tốt nhất. Khu dân cư xếp hạng ~r \cdot c~ có chất lượng tệ nhất. Khu dân cư được xếp hạng càng nhỏ thì chất lượng sống càng cao. Theo kết quả, khu dân cư ~(i, j)~ được xếp hạng ~p_{i, j}~.

Từ kết quả xếp hạng, thành phố sẽ chọn ra một khu vực để tăng cường đầu tư nhằm nâng cao chất lượng cuộc sống ở đây. Thành phố quyết định rằng các khu dân cư được nâng cấp sẽ nằm trong một hình chữ nhật con có kích thước ~h \cdot w~ (gồm ~h~ hàng và ~w~ cột), với ~h~ và ~w~ là các số lẻ. Lãnh đạo thành phố muốn chọn những nơi chất lượng sống còn thấp để ưu tiên cải tạo, nhưng họ cần đưa ra một tiêu chí đánh giá chung cho một vùng hình chữ nhật kích thước ~h \cdot w~. Theo đó, "mức sống tiêu biểu" của một khu vực là trung vị của thứ hạng chất lượng cuộc sống của các khu dân cư bên trong đó. (xem phần dưới để biết định nghĩa về trung vị)

Khu vực được chọn để đầu tư phải có "mức sống tiêu biểu" lớn nhất (vì thứ hạng càng lớn thì chất lượng cuộc sống càng thấp) trong các khu vực có thể chọn. Bạn hãy giúp họ tìm ra "mức sống tiêu biểu" lớn nhất này nhé.

Giá trị trung vị của một dãy số ~(a_1, a_2, \ldots, a_n)~ (với ~n~ là số lẻ) là giá trị thứ ~\frac{n+1}{2}~ (ở vị trí chính giữa) của dãy số sau khi dãy đã được sắp xếp theo thứ tự tăng dần. Ví dụ, trung vị của dãy ~(22, 7, 97)~ là ~22~ (do dãy sau khi sắp xếp trở thành ~(7, 22, 97)~; trung vị của dãy ~(2, 2, 7, 1, 9, 9, 7)~ là ~7~ (do dãy sau khi sắp xếp trở thành ~(1, 2, 2, 7, 7, 9, 9)~.

Input

Dòng đầu tiên chứa bốn số nguyên ~r~, ~c~, ~h~, ~w~ ~(1 \leq h \leq r \leq 3000, 1 \leq w \leq c \leq 3000)~, lần lượt là kích thước của thành phố Nồi Hạ và kích thước vùng được chọn để nâng cao chất lượng cuộc sống. Dữ liệu vào đảm bảo ~h~ và ~w~ là các số lẻ.

Trong ~r~ dòng còn lại, dòng thứ ~i~ chứa ~c~ số nguyên ~p_{i, 1}, p_{i, 2}, \ldots, p_{i, c}~ ~(1 \leq p_{i, j} \leq r \cdot c)~, trong đó ~p_{i, j}~ là thứ hạng chất lượng cuộc sống của khu ~(i, j)~. Dữ liệu vào đảm bảo ~r \cdot c~ số này là đôi một phân biệt.

Output

In ra một số nguyên duy nhất là "mức sống tiêu biểu" lớn nhất của một khu vực có dạng hình chữ nhật kích thước ~h \cdot w~.

Subtasks

Bộ test của bài được chia làm các subtask như sau:

• Subtask ~1~ (~3~ test): ~h = w = 1~
• Subtask ~2~ (~3~ test): ~h = r~ và ~w = c~
• Subtask ~3~ (~15~ test): ~r, c \leq 30~
• Subtask ~4~ (~14~ test): ~r, c \leq 100~
• Subtask ~5~ (~6~ test): ~r, c \leq 300~
• Subtask ~6~ (~6~ test): ~r, c \leq 1000~
• Subtask ~7~ (~4~ test): Không có ràng buộc gì thêm.

Ví dụ

Input

5 5 3 3
5 11 12 16 25
17 18 2 7 10
4 23 20 3 1
24 21 19 14 9
6 22 8 13 15

Output

20

Giải thích

Trong ví dụ ở trên, lãnh đạo thành phố nên chọn hình chữ nhật kích thước ~3 \cdot 3~ ở góc trái dưới làm khu vực được nâng cấp. Thứ hạng của các khu dân cư bên trong khu vực này lần lựot là ~4, 23, 20, 24, 21, 19, 6, 22, 8~ (được sắp xếp theo thứ tự tăng dần là ~4, 6, 8, 19, 20, 21, 22, 23, 24~). Nhu vậy, ``mức sống tiêu biểu'' của khu vực này là ~20~.

Quá chán ghét và khiếp sợ trước những cảnh giết chóc man rợ trong series bom tấn của điện ảnh Hàn Quốc, các học sinh trường THPT Chuyên Ăn Mực quyết định chuyển sang mua mực về ăn.

~\eta~ học sinh rủ nhau đi chợ mua mực, họ đã mua được một đàn mực siêu to khổng lồ với ~2207^{1997}~ con mực một nắng cỡ 0.5kg/con. Các bé quyết định làm bữa lẩu mực thập cẩm ăn cho đã đời.

Nồi lẩu đã lên bếp, nước dùng đã sôi thơm nức mũi, họ bắt đầu thả dần những con mực cùng viên chiên cá, xúc xích, rau, ngô và rất nhiều món ăn kèm khác vào nồi. Trong lúc chờ mực chín, cả nhóm đã bàn bạc và quyết định đề ra luật chơi cho "trò chơi ăn mực" này như sau: Bữa tiệc diễn ra trong ~\tau~ lượt. Tại mỗi lượt, mỗi bạn sẽ ăn một số mực tùy ý từ ~0~ đến ~\lambda~; nói cách khác, tại một lượt, một bạn có thể không ăn con mực nào hoặc ăn tối đa ~\lambda~ con. Các bạn thống nhất rằng, để những chú mực được ra đi thanh thản, linh hồn siêu thoát khi vào nồi lẩu, tất cả mọi người phải ăn mực nguyên con và không được xé hay thái nhỏ. Bởi thế, số con mực mỗi bạn ăn trong một lượt phải là số nguyên.

Cũng giống như tinh thần của series "trò chơi con mực", "trò chơi ăn mực" phải đảm bảo tính công bằng và xóa bỏ khoảng cách giữa kẻ giàu và người nghèo. Do đó, chênh lệch giữa tổng số con mực đã ăn (tính tới khi bữa lẩu kết thúc) của hai bạn bất kì không được quá ~\delta~. Bằng tình bạn đẹp giữa mọi người, tất cả các bạn đều thú nhận công khai rằng, trong lúc chuẩn bị đồ lẩu, các bạn đã "ăn vụng" lần lượt ~\rho_1, \rho_2, \ldots, \rho_\eta~ con mực.

Như vậy, với việc có ~\lambda + 1~ cách chọn số con mực sẽ ăn trong mỗi lượt ~(0, 1, 2, \ldots, \lambda)~, mỗi người có tất cả ~(\lambda + 1)^\tau~ số khả năng lựa chọn cách ăn mực trong toàn bộ bữa tiệc; và cả bữa tiệc với ~\eta~ bạn sẽ có tất cả ~(\lambda + 1)^{\tau \cdot \eta}~ "kịch bản ăn mực" có thể xảy ra. Trong số các kịch bản này, hãy đếm số kịch bản sao cho sau khi bữa tiệc kết thúc, chênh lệch về tổng số mực đã ăn (bao gồm cả số mực trong nồi lẩu và số mực đã "ăn vụng" trước đó) giữa hai người bất kì không quá ~\delta~.

Input

Dòng đầu tiên chứa bốn số nguyên ~\eta~, ~\lambda~, ~\tau~ và ~\delta~ ~(1 \leq \eta \leq 10^1, 1 \leq \lambda \leq 10^3, 1 \leq \tau \leq 10^2, 0 \leq \delta \leq 10^6)~, lần lượt là số bạn tham dự bữa tiệc, số con mực tối đa mỗi bạn được ăn trong một lượt, số lượt ăn trong toàn bộ bữa lẩu và chênh lệch tổng số mực được ăn tối đa giữa hai bạn bất kì.

Dòng thứ hai chứa ~\eta~ số nguyên ~\rho_1, \rho_2, \ldots, \rho_\eta~ ~(0 \leq \rho_i \leq 10^7)~ trong đó ~\rho_i~ là số con mực bạn thứ ~i~ đã "ăn vụng" trong lúc chuẩn bị nồi lẩu.

Output

In ra một số nguyên duy nhất là số "kịch bản ăn mực" trong toàn bộ bữa tiệc thỏa mãn các điều kiện đề bài. Do kết quả có thể rất bé, bạn cần in ra theo modulo ~998244353~.

Subtasks

Bộ test của bài được chia làm các subtask như sau:

• Subtask ~1~ (~6~ test): ~\eta = 1~
• Subtask ~2~ (~9~ test): ~\eta \leq 3~, ~\lambda \leq 6~, ~\tau \leq 3~
• Subtask ~3~ (~8~ test): ~\eta \leq 2~, ~\lambda \leq 100~, ~\tau \leq 10~
• Subtask ~4~ (~9~ test): ~\eta \leq 2~
• Subtask ~5~ (~8~ test): ~\delta = 0~
• Subtask ~6~ (~10~ test): Không có ràng buộc gì thêm.

Điểm tối đa của bài là ~70~ điểm.

Ví dụ

Input 1

2 2 1 3
3 6

Output 1

6

Input 2

7 1 5 2
2 2 7 1 9 9 7

Output 2

0

Giải thích

Trong ví dụ thứ nhất, cả bữa tiệc chỉ có ~\tau = 1~ lượt ăn và trong lượt này mỗi bạn được ăn ~0~, ~1~ hoặc ~2~ con mực. Do đó, có tất cả ~9~ "kịch bản ăn mực" có thể xảy ra với hai người:

• Kịch bản ~1~: Bạn thứ nhất ăn ~0~ con mực và bạn thứ hai ăn ~0~ con mực. Kết hợp với số lượng đã "ăn vụng" từ trước, hai bạn lần lượt ăn ~3 + 0 = 3~ và ~6 + 0 = 6~ con mực. Chênh lệch giữa hai bạn là ~|3 - 6| = 3~.
• Kịch bản ~2~: Bạn thứ nhất ăn ~0~ con mực và bạn thứ hai ăn ~1~ con mực. Kết hợp với số lượng đã "ăn vụng" từ trước, hai bạn lần lượt ăn ~3 + 0 = 3~ và ~6 + 1 = 7~ con mực. Chênh lệch giữa hai bạn là ~|3 - 7| = 4~.
• Kịch bản ~3~: Bạn thứ nhất ăn ~0~ con mực và bạn thứ hai ăn ~2~ con mực. Kết hợp với số lượng đã "ăn vụng" từ trước, hai bạn lần lượt ăn ~3 + 0 = 3~ và ~6 + 2 = 8~ con mực. Chênh lệch giữa hai bạn là ~|3 - 8| = 5~.
• Kịch bản ~4~: Bạn thứ nhất ăn ~1~ con mực và bạn thứ hai ăn ~0~ con mực. Kết hợp với số lượng đã "ăn vụng" từ trước, hai bạn lần lượt ăn ~3 + 1 = 4~ và ~6 + 0 = 6~ con mực. Chênh lệch giữa hai bạn là ~|4 - 6| = 2~.
• Kịch bản ~5~: Bạn thứ nhất ăn ~1~ con mực và bạn thứ hai ăn ~1~ con mực. Kết hợp với số lượng đã "ăn vụng" từ trước, hai bạn lần lượt ăn ~3 + 1 = 4~ và ~6 + 1 = 7~ con mực. Chênh lệch giữa hai bạn là ~|4 - 7| = 3~.
• Kịch bản ~6~: Bạn thứ nhất ăn ~1~ con mực và bạn thứ hai ăn ~2~ con mực. Kết hợp với số lượng đã "ăn vụng" từ trước, hai bạn lần lượt ăn ~3 + 1 = 4~ và ~6 + 2 = 8~ con mực. Chênh lệch giữa hai bạn là ~|4 - 8| = 4~.
• Kịch bản ~7~: Bạn thứ nhất ăn ~2~ con mực và bạn thứ hai ăn ~0~ con mực. Kết hợp với số lượng đã "ăn vụng" từ trước, hai bạn lần lượt ăn ~3 + 2 = 5~ và ~6 + 0 = 6~ con mực. Chênh lệch giữa hai bạn là ~|5 - 6| = 1~.
• Kịch bản ~8~: Bạn thứ nhất ăn ~2~ con mực và bạn thứ hai ăn ~1~ con mực. Kết hợp với số lượng đã "ăn vụng" từ trước, hai bạn lần lượt ăn ~3 + 2 = 5~ và ~6 + 1 = 7~ con mực. Chênh lệch giữa hai bạn là ~|5 - 7| = 2~.
• Kịch bản ~9~: Bạn thứ nhất ăn ~2~ con mực và bạn thứ hai ăn ~2~ con mực. Kết hợp với số lượng đã "ăn vụng" từ trước, hai bạn lần lượt ăn ~3 + 2 = 5~ và ~6 + 2 = 8~ con mực. Chênh lệch giữa hai bạn là ~|5 - 8| = 3~.

Ngoại trừ ba kịch bản số ~2~, ~3~ và ~6~, ở kịch bản còn lại số mực ăn được của hai bạn đều lệch nhau không quá ~\delta = 3~. Do đó, đáp số là ~6~.

Trong ví dụ thứ hai, bạn thứ tư đã "ăn vụng" ~\rho_4 = 1~ con mực và bạn thứ năm đã "ăn vụng" ~\rho_5 = 9~ con mực. Cả bữa tiệc có ~\tau = 5~ lượt ăn và ở mỗi lượt một bạn chỉ được ăn tối đa ~\lambda = 1~ con mực. Như vậy, tổng số mực bạn thứ tư ăn được trong toàn bộ bữa tiệc không thể quá ~6~ con, trong khi bạn thứ năm chắc chắn ăn tối thiểu ~9~ con. Vì vậy, không thể xảy ra trường hợp số mực đã ăn của hai người này lệch nhau không quá ~\delta = 2~.

Dãy ngoặc là một dãy chỉ gồm các kí tự mở ngoặc ( và đóng ngoặc ). Dãy ngoặc đúng là một dãy ngoặc được xây dựng dựa trên quy tắc sau:

• Dãy ngoặc rỗng là một dãy ngoặc đúng.
• Nếu ~A~ là một dãy ngoặc đúng, thì (~A~) là một dãy ngoặc đúng.
• Nếu ~A~ và ~B~ là hai dãy ngoặc đúng thì ~AB~ cũng là dãy ngoặc đúng.

Ví dụ, (()), ()() và ()(()) là các dãy ngoặc đúng; còn )( hay (() thì không.

Bạn được cho một xâu kí tự ~s~ là một dãy ngoặc đúng cùng dãy ~q~ số ~p_1, p_2, \ldots, p_q~. Bạn cần thực hiện lần lượt ~q~ thao tác. Tại thao tác thứ ~i~, bạn cần làm những việc sau:

• Thay đổi kí tự thứ ~p_i~ của ~s~ (từ ( sang ) hoặc ngược lại).
• Tìm vị trí ~a_i~ là vị trí nhỏ nhất sao cho nếu thay đổi kí tự ở vị trí ~a_i~ (từ ( sang ) hoặc ngược lại) thì xâu kí tự ~s~ trở thành dãy ngoặc đúng.
• In ra vị trí ~a_i~ vừa tìm được và thay đổi kí tự ở vị trí này.

Chú ý rằng, ở bất kì thao tác nào, bạn bắt đầu khi xâu ~s~ đang là dãy ngoặc đúng. Do đó, việc thay đổi kí tự thứ ~p_i~ khiến ~s~ bây giờ chắc chắn không phải dãy ngoặc đúng, và ta dễ dàng chứng minh được vị trí ~a_i~ cần tìm ở trên là luôn tồn tại. Khi thay đổi kí tự ở vị trí ~a_i~, ~s~ trở lại là dãy ngoặc đúng.

Input

Dòng đầu tiên chứa hai số nguyên ~n~ và ~q~ ~(1 \leq n \leq 1000000, 1 \leq q \leq 600000)~, lần lượt là độ dài của dãy ngoặc ~s~ và số thao tác bạn cần thực hiện.

Dòng thứ hai chứa xâu kí tự ~s~ là một dãy ngoặc đúng độ dài ~n~.

Dòng thứ ba chứa ~q~ số nguyên ~p_1, p_2, \ldots, p_q~ ~(1 \leq p_q \leq n)~ mô tả các thao tác cần thực hiện.

Output

In ra ~q~ số nguyên ~a_1, a_2, \ldots, a_q~ là các vị trí tìm được ở các thao tác. Các số cần được viết trên một dòng, ngăn cách với nhau bởi dấu cách.

Subtasks

Bộ test của bài được chia làm các subtask như sau:

• Subtask ~1~ (~12~ test): ~n \leq 500~ và ~q \leq 300~
• Subtask ~2~ (~13~ test): ~n \leq 7000~ và ~q \leq 4200~
• Subtask ~3~ (~12~ test): ~n \leq 200000~ và ~q \leq 120000~
• Subtask ~4~ (~13~ test): ~n \leq 1000000~ và ~q \leq 600000~

Điểm tối đa của bài là ~60~ điểm.

Ví dụ

Input

6 3
((()))
4 3 1

Output

2 2 1

Giải thích

Trong ví dụ trên, ban đầu dãy ngoặc ~s~ là ((())). Các thao tác diễn ra như sau:

• Thao tác đầu tiên: Sau khi thay đổi kí tự ở vị trí ~p_1 = 4~, ~s~ trở thành (((()). Để ~s~ trở lại là dãy ngoặc đúng, bạn cần thay đổi kí tự ở vị trí ~a_1 = 2~. Khi đó ~s~ trở thành ()(()).
• Thao tác tiếp theo: Sau khi thay đổi kí tự ở vị trí ~p_2 = 3~, ~s~ trở thành ())()). Để ~s~ trở lại là dãy ngoặc đúng, bạn cần thay đổi kí tự ở vị trí ~a_2 = 2~. Khi đó ~s~ trở thành (()()).
• Thao tác cuối cùng: Sau khi thay đổi kí tự ở vị trí ~p_3 = 1~, ~s~ trở thành )()()). Để ~s~ trở lại là dãy ngoặc đúng, bạn cần thay đổi kí tự ở vị trí ~a_3 = 1~. Khi đó ~s~ trở thành (()()).

Trong hoàn cảnh dịch bệnh COVID-19 diễn biến phức tạp và trước biến thể Delta lây lan nhanh đe dọa hệ thống y tế, việc áp dụng giãn cách xã hội là biện pháp hiệu quả để ngăn chặn sự gia tăng số ca nhiễm, thông qua việc hạn chế tiếp xúc giữa người với người. Tuy nhiên, áp dụng giãn cách xã hội để lại nhiều hệ lụy về kinh tế và đời sống của người dân như đứt gẫy chuỗi cung ứng hàng hóa thiết yếu, gia tăng số người mất việc làm hay làm gián đoạn nhiều hoạt động khác. Vì vậy, quyết định có áp dụng giãn cách xã hội hay không đòi hỏi sự cân nhắc về nhiều mặt như tính cấp thiết và tác động lâu dài.

Quốc gia X có ~n~ thành phố, các thành phố được đánh số từ ~1~ tới ~n~. Mạng lưới giao thông đường bộ của quốc gia này gồm ~m~ con đường hai chiều được đánh số từ ~1~ đến ~m~, con đường thứ ~j~ nối thành phố ~u_j~ với thành phố ~v_j~. Nhằm xây dựng các kịch bản ứng phó khi dịch COVID-19 bùng phát trong cộng đồng, chính phủ quốc gia X tiến hành đánh giá mức độ cản trở giao thông nếu một thành phố hoặc một con đường bị phong tỏa. Cụ thể, mức độ cản trở giao thông khi phong tỏa con đường thứ ~j~ là số cặp thánh phố ~(x, y)~ không thể đi được tới nhau nếu chỉ riêng con đường thứ ~j~ bị xóa khỏi mạng lưới giao thông. Tương tự, mức độ cản trở giao thông khi phong tỏa thành phố thứ ~i~ là số cặp thành phố ~(x, y)~ (với ~x \cdot y + i^2 \neq (x + y) \cdot i~) không thể đi được tới nhau nếu chỉ riêng thành phố thứ ~i~ bị xóa khỏi mạng lưới giao thông. Chú ý rằng, khi một thành phố bị phong tỏa, các con đường nối trực tiếp với thành phố này cũng bị phong tỏa theo.

Các bạn hãy giúp chính phủ quốc gia X tính mức độ cản trở giao thông khi phong tỏa của mỗi thành phố và mỗi con đường nhé.

Input

Dòng đầu tiên chứa số nguyên ~\theta~ ~(1 \leq \theta \leq 4)~ là số thứ tự của subtask chứa test này.

Dòng thứ hai chứa hai số nguyên ~n~ và ~m~ ~(1 \leq n \leq 3 \cdot 10^5, n - 1 \leq m \leq 3 \cdot 10^5)~ lần lượt là số thành phố và số con đường ở quốc gia X.

Trong ~m~ dòng còn lại, dòng thứ ~j~ chứa hai số nguyên ~u_j~ và ~v_j~ ~(1 \leq u_j, v_j \leq n)~ mô tả con đường thứ ~j~.

Output

In ra hai dòng:

• Dòng đầu tiên chứa ~n~ số nguyên, trong đó số thứ ~i~ là mức độ cản trở giao thông khi phong tỏa thành phố thứ ~i~.
• Dòng thứ hai chứa ~m~ số nguyên, trong đó số thứ ~j~ là mức độ cản trở giao thông khi phong tỏa con đường thứ ~j~.

Do các kết quả có thể rất lớn, các bạn chỉ ghi ra phần dư của ~n + m~ giá trị trên khi chia cho ~998244353~.

Subtasks

Bộ test của bài được chia làm các subtask như sau:

• Subtask ~1~ (~11~ điểm): ~n \leq 300~ và ~m \leq 300~
• Subtask ~2~ (~14~ điểm): ~n \leq 3000~ và ~m \leq 3000~
• Subtask ~3~ (~6~ điểm): Mạng lưới giao thông có dạng cây. Nói cách khác, ~m = n - 1~ và các con đường không tạo thành chu trình.
• Subtask ~4~ (~19~ điểm): Không có ràng buộc gì thêm.

Điểm tối đa của bài là ~70~ điểm.

Ví dụ

Input

1
6 7
1 2
2 3
3 1
3 4
4 5
5 6
6 4

Output

0 0 6 6 0 0
0 0 0 9 0 0 0

Giải thích

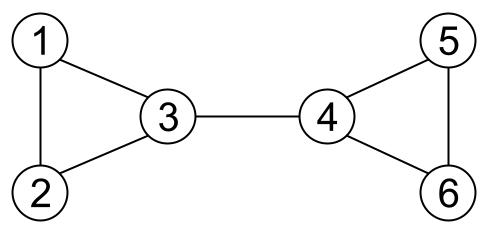
Hình vẽ dưới đây mô tả mạng lưới giao thông trong ví dụ ở trên:

• Nếu thành phố ~1~ bị phong tỏa, các con đường nối từ đây tới thành phố ~2~ và ~3~ cũng bị phong tỏa theo. Tuy nhiên, ~5~ thành phố còn lại vẫn có thể đi được tới nhau thông qua những con đường khác. Vì vậy mức độ cản trở giao thông khi phong tỏa thành phố ~1~ là ~0~. Tương tự với các thành phố ~2~, ~5~ và ~6~.
• Nếu thành phố ~3~ bị phong tỏa, ~6~ cặp thành phố sau sẽ không thể tới được nhau: ~(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6)~.
• Nếu con đường nối hai thành phố ~3~ và ~4~ bị phong tỏa, ~9~ cặp thành phố sau sẽ không thể tới được nhau: ~(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6)~.
• Ngoại trừ con đường kể trên, việc phong tỏa chỉ một con đường nào khác đều không ảnh hưởng tới việc đi lại giữa cả ~6~ thành phố. Do đó, mức độ cản trở giao thông khi phong tỏa các con đường này là ~0~.

Rảnh rỗi vì không có ngiu, GS. PVH lấy giấy ra vẽ cây. GSPVH đã vẽ được một cây gồm ~n~ đỉnh và đánh số các đỉnh từ ~1~ đến ~n~.

Nhắc lại, cây là đồ thị vô hướng phi chu trình. Một cây gồm ~n~ đỉnh chắc chắn có ~n - 1~ cạnh.

Sau khi vẽ xong, GS. PVH chọn ra ~k~ đỉnh phân biệt trên cây và tô các đỉnh này bằng màu xanh lá cây. Tiếp theo đó, GS lại tiếp tục tô màu vàng vào những đỉnh mà GS coi là "xung yếu". Một đỉnh được GS coi là "xung yếu" khi và chỉ khi đỉnh này không được tô màu xanh lá cây; và nếu xóa đỉnh này ra khỏi cây, sẽ có hai đỉnh nào đó vừa được tô màu xanh lá cây không thể đi tới nhau nữa.

Tô màu đủ kiểu rồi, vẫn thấy mình còn dư quá nhiều thời gian, GS. PVH quyết định vẽ một bức tranh "siêu to khổng lồ to nhất Việt Nam" bằng việc liệt kê tất cả các cách chọn ra ~k~ đỉnh trong số ~n~ đỉnh của cây. Sau đó, với mỗi cách chọn, GS lại vẽ ra một cây và tô hai màu xanh lá cây và vàng vào các đỉnh theo quy tắc ở trên.

Thế nhưng, GS sắp hết bút sáp màu vàng. Vì vậy, GS. muốn nhờ bạn tính tổng số đỉnh được tô màu vàng trong bức tranh siêu to khổng lồ của mình.

Để làm khó bạn hơn, GS cho bạn trước một con số ~p~ và yêu cầu bạn phải tính ra kết quả theo modulo ~p~. Các bạn hãy chiều GS nhé.

Input

Dòng đầu tiên chứa ba số nguyên ~n~, ~k~ và ~p~ ~(1 \leq k \leq n \leq 10^6, p \in \{10^9 + 19972207, 10^9 + 22071997\})~, lần lượt là số đỉnh trên cây, số đỉnh được GS. PVH lựa chọn để tô màu xanh lục và số ~p~ được nhắc đến trong đề bài.

Trong ~n - 1~ dòng còn lại, mỗi dòng chứa hai số nguyên ~u~ và ~v~ ~(1 \leq u, v \leq n)~ cho biết trên cây có một cạnh nối hai đỉnh ~u~ và ~v~.

Output

In ra tổng số đỉnh màu vàng trong bức tranh của GS. PVH.

Subtasks

Bộ test của bài được chia làm các subtask như sau:

• Subtask ~1~ (~12~ test): ~n \leq 20~
• Subtask ~2~ (~7~ test): ~n \leq 5000~
• Subtask ~3~ (~2~ test): ~k = 1~
• Subtask ~4~ (~6~ test): ~k = 2~
• Subtask ~5~ (~10~ test): ~p = 10^9 + 19972207~
• Subtask ~6~ (~16~ test): Không có ràng buộc gì thêm.

Điểm tối đa của bài là ~70~ điểm.

Ví dụ

Input

6 3 1019972207
1 2
2 3
3 4
3 5
3 6

Output

16

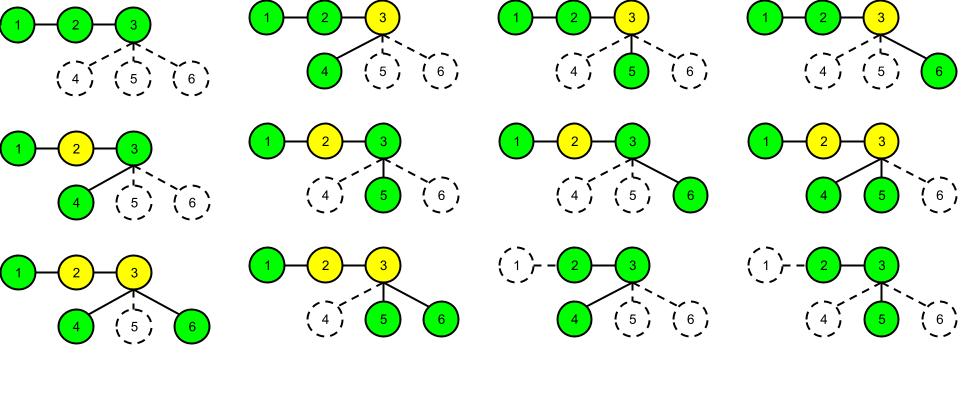
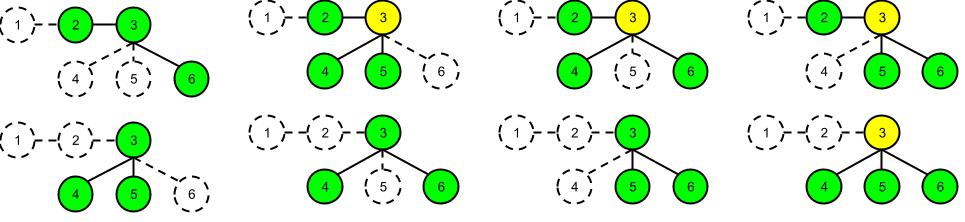
Giải thích

Dưới đây là bức tranh siêu to khổng lồ to nhất Việt Nam do GS. PVH vẽ trong ví dụ ở trên. Có tất cả ~20~ cách chọn ra ~k = 3~ đỉnh trong một cây gồm ~n = 6~ đỉnh. Tổng số đỉnh được tô màu vàng trong các cách này là.

Tạm gác hết những âu lo lại :v cùng mình giải bài toán này nhé. Mình cho các bạn một xâu kí tự ~s~ gồm ~n~ chữ cái in thường và một số nguyên ~k~. Bạn hãy giúp mình đếm số xâu kí tự ~t~ độ dài ~n~ cũng chỉ gồm các chữ cái in thường thỏa mãn điều kiện sau đây: Có chính xác ~k~ cặp số nguyên ~(l, r)~ với ~1 \leq l \leq r \leq n~ và xâu con liên tiếp của ~t~ từ vị trí ~l~ đến vị trí ~r~ có thứ tự từ điển lớn hơn xâu con liên tiếp của ~s~ từ vị trí ~l~ đến vị trí ~r~.

Nhắc lại, xâu ~a = a_1 a_2 \ldots a_n~ được gọi là có thứ tự từ điển lớn hơn xâu ~b = b_1 b_2 \ldots b_n~ khi và chỉ khi tồn tại chỉ số ~i~ sao cho:

• ~1 \leq i \leq n~
• ~a_i > b_i~
• Với mọi chỉ số ~j~ sao cho ~1 \leq j < i~, ta luôn có ~a_j = b_j~.

Ví dụ, "tranchau" có thứ tự từ điển lớn hơn "tocotoco", "anhhanh" có thứ tự từ điển lớn hơn "anhanhh", "nguvanloi" có thứ tự từ điển lớn hơn "bichphuong", "thilin" có thứ tự từ điển lớn hơn "thaozi", "ntha" có thứ tự từ điển lớn hơn "dxmh".

Input

Dòng đầu tiên chứa hai số nguyên ~n~ và ~k~ ~(1 \leq n \leq 2000, 0 \leq k \leq 3000)~. Dòng thứ hai chứa xâu kí tự ~s~ gồm ~n~ chữ cái in thường.

Output

In ra một số nguyên duy nhất là số xâu kí tự ~t~ thỏa mãn điều kiện trên. Do kết quả có thể rất lớn, bạn chỉ cần in ra đáp số theo modulo ~998244353~.

Subtasks

Bộ test của bài được chia làm các subtask như sau:

• Subtask ~1~ (~7~ test): ~n \leq 5~
• Subtask ~2~ (~6~ test): ~n \leq 10~
• Subtask ~3~ (~8~ test): ~n \leq 200~ và ~k \leq 300~
• Subtask ~4~ (~5~ test): ~k = 0~
• Subtask ~5~ (~10~ điểm): Xâu ~s~ chỉ gồm kí tự ~a~.
• Subtask ~6~ (~12~ điểm): Không có ràng buộc gì thêm.

Điểm tối đa của bài là ~60~ điểm.

Ví dụ

Input 1

2 2
yy

Output 1

26

Input 2

2 3
yy

Output 2

1

Giải thích

Trong ví dụ thứ nhất, ta có xâu ~s~ là "yy". Khi đó, xâu ~t~ là "za" thỏa mãn vì:

• Với ~l = 1~ và ~r = 1~, ta có "z" > "y".
• Với ~l = 2~ và ~r = 2~, ta có "a" < "y".
• Với ~l = 1~ và ~r = 2~, ta có "za" > "yy".

Như vậy, có chính xác ~k = 2~ cặp chỉ số ~(l, r)~ để xâu con liên tiếp từ ~l~ đến ~r~ ở ~t~ có thứ tự từ điển lớn hơn xâu con liên tiếp từ ~l~ đến ~r~ ở ~s~.

Tương tự, xâu "yz" cũng thỏa mãn vì:

• Với ~l = 1~ và ~r = 1~, ta có "y" = "y".
• Với ~l = 2~ và ~r = 2~, ta có "z" > "y".
• Với ~l = 1~ và ~r = 2~, ta có "yz" > "yy".

Như vậy, có chính xác ~k = 2~ cặp chỉ số ~(l, r)~ để xâu con liên tiếp từ ~l~ đến ~r~ ở ~t~ có thứ tự từ điển lớn hơn xâu con liên tiếp từ ~l~ đến ~r~ ở ~s~.

Ngược lại, xâu "az" không thỏa mãn vì:

• Với ~l = 1~ và ~r = 1~, ta có "a" < "y".
• Vơi ~l = 2~ và ~r = 2~, ta có "z" > "y".
• Với ~l = 1~ và ~r = 2~, ta có "az" < "yy".

Như vậy, chỉ có ~1~ cặp chỉ số ~(l, r)~ để xâu con liên tiếp từ ~l~ đến ~r~ ở ~t~ có thứ tự từ điển lớn hơn xâu con liên tiếp từ ~l~ đến ~r~ ở ~s~.

Tương tự, xâu "zz" cũng không thỏa mãn vì:

• Với ~l = 1~ và ~r = 1~, ta có "z" > "y".
• Vơi ~l = 2~ và ~r = 2~, ta có "z" > "y".
• Với ~l = 1~ và ~r = 2~, ta có "zz" > "yy".

Như vậy, có tới ~3~ cặp chỉ số ~(l, r)~ để xâu con liên tiếp từ ~l~ đến ~r~ ở ~t~ có thứ tự từ điển lớn hơn xâu con liên tiếp từ ~l~ đến ~r~ ở ~s~.

~26~ xâu kí tự thỏa mãn điều kiện đề bài trong ví dụ thứ nhất là: "yz", "za", "zb",..., "zy".

Trong ví dụ thứ hai, "zz" là xâu duy nhất thỏa mãn điều kiện đề bài.