Công ty bánh kẹo ABC chuẩn bị xây dựng hệ thống đại lý để giao bánh kẹo đến tất cả địa điểm trong thành phố. Hàng ngày, từ mỗi đại lý các nhân viên dùng ~K~ loại xe với trọng lượng lần lượt là ~P_1,\ P_2,...,\ P_K~ chuyên chở bánh kẹo đến các địa điểm còn lại.

Thành phố có ~N~ địa điểm (đánh số từ ~1~ đến ~N~) và ~M~ con đường hai chiều nối trực tiếp giữa các địa điểm, trên mỗi con đường có ghi một số nguyên dương cho biết trọng lượng tối đa của xe được phép di chuyển trên con đường này. Giữa ~2~ địa điểm bất kì có thể có nhiều con đường nối trực tiếp.

Để có thể giao hàng đến ~N~ địa điểm, công ty tìm cách chọn một số địa điểm để đặt đại lý. Chi phí mỗi cách chọn phụ thuộc vào số lượng địa điểm được chọn làm đại lý, số địa điểm càng ít thì chi phí càng thấp.

Yêu cầu: Hãy cho biết cách chọn có chi phí thấp nhất sẽ có số lượng địa điểm đặt đại lý là bao nhiêu.

Input

Cho trong file văn bản BANHKEO.INP.

• Dòng đầu tiên gồm ba số nguyên dương ~N\ (1 \le N \le 1000),\ M\ (1 \le M \le 100000),\ K (1 \le K \le 20)~.

• Dòng thứ hai gồm ~K~ số nguyên dương ~P_1,\ P_2,...,\ P_K\ (1 \le P_i \le 500)~

• ~M~ dòng tiếp theo, dòng thứ ~i~ gồm ba số nguyên dương ~A_i,\ B_i,\ T_i\ (1 \le Ti \le 500)~, cho biết con đường nối giữa địa điểm Ai đến Bi chịu được trọng lượng tối đa là ~T_i~. Các số ghi trên cùng một dòng cách nhau bởi ít nhất một kí tự trắng.

Output

Ghi ra file văn bản BANHKEO.OUT gồm một dòng với số nguyên duy nhất cho biết số lượng địa điểm ít nhất.

Sample Input 1

5 6 3
5 3 4
1 2 2
1 3 1
2 3 3
3 4 2
4 5 2
4 5 4

Sample Output 1

3

Notes

Công ty có ba loại xe với trọng lượng ~5,\ 3,\ 4~. Bằng cách chọn ba địa điểm ~1,\ 3,\ 5~ để đặt đại lý. Công ty có thể giao bánh kẹo đến tất cả các địa điểm.

Phú hộ qua đời để lại cho 4 người con một mảnh đất hình vuông có kích thước ~n \times n~, trên đó có trồng một số cây gỗ quí. Theo di chúc, mảnh đất sẽ được chia thành ~4~ phần, mỗi phần là một hình chữ nhật. Để tiết kiệm chi phí chia đất nên chỉ có thể thực hiện cắt mảnh đất bởi một nhát cắt theo chiều ngang và một nhát cắt theo chiều dọc. Các con của phú hộ đều thích có nhiều cây gỗ quí vì vậy họ sẽ chọn phần đất có nhiều cây gỗ quí hơn. Thứ tự nhận đất sẽ từ lớn tới nhỏ, người em út sẽ nhận phần có ít cây gỗ quí nhất.

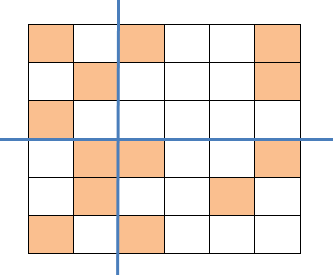
Yêu cầu: Hãy chỉ cách chia đất để chênh lệch giữa số cây gỗ quí của người anh cả và của người em út là ít nhất.

Input

Cho từ tệp văn bản CHIADAT.INP có định dạng:

• Dòng thứ nhất ghi số nguyên dương ~n~ (~2 \le n \le 500~).
• Tiếp theo là ~n~ dòng, mỗi dòng ghi ~n~ số, số ~0~ hoặc số ~1~. Số ~0~ thể hiện vị trí không có cây gỗ quí, số ~1~ thể hiện vị trí có cây gỗ quí.
• Các số ghi trên cùng một dòng cách nhau bởi ít nhất một kí tự trắng.

Output

Ghi vào tệp văn bản CHIADAT.OUT chỉ có một dòng ghi một số nguyên là số lượng chênh lệch cây gỗ quí ít nhất trên phần đất của người anh cả và của người em út.

Ràng buộc

• Có ~50\%~ số test tương ứng ~50\%~ số điểm có ~2 \le n \le 150~.
• Có ~50\%~ số test tương ứng ~50\%~ số điểm có ~150 < n \le 500~.

Sample Input 1

6
1 0 1 0 0 1
0 1 0 0 0 1
1 0 0 0 0 0
0 1 1 0 0 1
0 1 0 0 1 0
1 0 1 0 0 0

Sample Output 1

1

Sân golf được biểu diễn bởi một lưới kích thước ~M \times N (1≤M, N≤500)~. Mỗi ô của lưới có độ cao trong khoảng ~0~ đến ~10^9~ so với mực nước biển.

Tại một vài ô trong lưới này là các vị trí có đặt lỗ, tức là nơi vận động viên sẽ đánh bóng rơi vào đó và bắt buộc sẽ đi đến đó để nhặt bóng.

Ban tổ chức của Olympics muốn đánh giá độ chênh lệch độ cao D của sân golf bằng cách làm như sau:

Cho một nhân viên bắt đầu di chuyển từ một vị trí đặt lỗ bất kỳ đến một trong bốn ô kề cạnh với ô đang đứng, có trị tuyệt đối chênh lệch độ cao không quá ~D~. Tại ô mới này, anh ta lại di chuyển tiếp sang một trong bốn ô kề cạnh có trị tuyệt đối chênh lệch độ cao không quá D. Cứ thế tiếp tục cho đến khi có thể đến được tất cả các lỗ.

Yêu cầu: Hãy xác định độ chênh lệch độ cao ~D~ nhỏ nhất mà từ một lỗ bất kỳ có thể đến được tất cả các lỗ còn lại.

Input

Từ file GOLF.INP gồm:

• Dòng ~1~: chứa ~2~ số nguyên ~M, N~.
• ~M~ dòng tiếp theo: mỗi dòng chứa ~N~ số nguyên là độ cao của ô.
• ~M~ dòng tiếp theo: mỗi dòng chứa ~N~ giá trị là ~0~ hoặc ~1~, trong đó ô có giá trị ~1~ cho biết tại vị trí đó có lỗ, ngược lại thì tại đó không có lỗ.

Các số ghi trên cùng một dòng cách nhau bởi ít nhất một kí tự trắng.

Output

Ghi ra file GOLF.OUT gồm ~1~ dòng duy nhất ghi số nguyên dương ~D~ cần tìm.

Sample Input 1

3 5
25 21 18 76 15
19 22 20 16 26
18 17 40 60 80
1 0 0 0 1
0 0 0 0 0
0 0 0 0 1

Sample Output 1

20

Notes

• Với ~D = 20~: từ lỗ ~(1,1)~ ta đến được các lỗ ~(1,5)~, ~(3,5)~ hoặc theo hướng ngược lại.
• Với ~D = 19~, từ lỗ ~(1,1)~ hoặc lỗ ~(1,5)~ ta không thể đi đến được lỗ ~(3,5)~.