Kỳ thi chọn Đội tuyển HSGQG Huế năm 2023-2024
Điểm: 100
Trong lập trình thi đấu, hai chủ đề thường được nhiều cao thủ ưa thích nhất đó là cây và lý thuyết số, bởi khi nghiên cứu các bài toán khó, thông thường người giải sẽ luôn tìm cách đơn giản hoá bài toán, sau đó sử dụng các kiến thức từ một trong hai lĩnh vực này làm hướng đi để giải quyết những phiên bản "dễ hơn" của bài toán gốc. Sau đây sẽ là một bài toán kết hợp cả hai lĩnh vực dễ và thú vị này.
Cho một cây gồm ~N~ đỉnh, có gốc cố định tại đỉnh ~1~. Mỗi đỉnh ~i~ chứa một số nguyên dương ~a_i~.
Định nghĩa:
~p(u)~ là tích của các số nguyên chứa trong các đỉnh nằm trong cây con gốc ~u~.
~\sigma_0(x)~ là số ước của ~x~.
Bạn được cho ~Q~ truy vấn, mỗi truy vấn là một đỉnh ~u~ (~1 \le u \le n~). Hãy xác định ~\sigma_0(p(u))~ ~mod~ ~10^9 + 7~.
Input
Nhập từ file TREE.INP:
Dòng 1: Hai số nguyên dương ~N, Q~.
Dòng 2: ~N~ số nguyên dương ~a_i~.
Dòng ~3 \rightarrow N + 1~: Mỗi dòng chứa hai số nguyên dương ~u_j, v_j~ thể hiện cạnh thứ của ~j~ cây.
Dòng ~N + 2~: ~Q~ số nguyên thể hiện lần lượt ~Q~ truy vấn.
Output
Xuất ra file TREE.OUT một dòng gồm ~Q~ số nguyên, mỗi số là đáp án của truy vấn tương ứng.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | ~18\%~ | ~N \le 10^3, Q \le 10^3, 1 \le a_i \le 10^5~ |
| ~2~ | ~12\%~ | ~N \le 10^5, Q \le 5, 1 \le a_i \le 10^5~ |
| ~3~ | ~20\%~ | ~N \le 10^5, Q \le 10^5, 1 \le a_i \le 3~ |
| ~4~ | ~24\%~ | ~N \le 10^5, Q \le 10^5, 1 \le a_i \le 10^5~, cây có dạng đường thẳng |
| ~5~ | ~26\%~ | ~N \le 10^5, Q \le 10^5, 1 \le a_i \le 10^5~ |
Sample Input 1
6 5
2 1 3 4 2 4
1 2
1 3
2 4
2 5
3 6
1 2 3 4 5
Sample Output 1
14 4 6 3 2
Notes
Xét ~u = 2~, ta có:
~p(2) = a_2 \cdot a_4 \cdot a_5 = 1 \cdot 4 \cdot 2 = 8~.
~\sigma_0(p(2)) = \sigma_0(8) = 4~.
Điểm: 100
Ribonucleic acid (RNA) là một phân tử polymer cơ bản có nhiều vai trò sinh học trong mã hóa, dịch mã, điều hòa, và biểu hiện của gene. RNA là một loại nucleic acid, và, cùng với lipid, protein và carbohydrate, tạo thành bốn loại đại phân tử cơ sở cho mọi dạng sự sống trên Trái Đất.
Giống như DNA, RNA tạo thành từ một chuỗi nucleotide, nhưng không giống DNA là thường tìm thấy nó ở dạng tự nhiên là một sợi đơn gập lại vào chính nó, hơn là sợi xoắn kép. Các sinh vật tế bào sử dụng RNA thông tin (mRNA) đề truyền đạt các thông tin di truyền (sử dụng các base nitric guanine, uracil, adenine, và cytosine, ký hiệu tương ứng bằng các chữ cái G, U, A và C) cho phép tổng hợp trực tiếp lên các protein chuyên biệt. Nhiều virus mã hóa thông tin di truyền của chúng trong bộ gene RNA.
Một nhà khoa học ~K~ muốn nghiên cứu các đặc tính của ~n~ chuỗi RNA khác nhau mà phòng thí nghiệm hiện có. Biết rằng các RNA có chung các nucleotide ở đầu hoặc ở cuối chuỗi thường sẽ có các tính chất tương tự nhau, ~K~ thực hiện ~m~ thao tác trích xuất RNA với các yêu cầu: ứng với một thao tác trích xuất, ~K~ cần thu thập tất cả các chuỗi RNA:
Nhận xâu ~P~ làm một tiền tố, và
Nhận xâu ~Q~ làm một hậu tố.
Trong đó, ~P~, ~Q~ là đặc trưng của thao tác trích xuất được cho trước.
Với mỗi một thao tác trích xuất, bạn hãy xác định giúp ~K~ rằng có bao nhiêu chuỗi RNA thoả mãn các yêu cầu trên.
Input
Dòng đầu tiên chứa hai số nguyên dương ~n, m~, cách nhau bởi một dấu cách (~1 \leq n, m \leq 10^5~).
~n~ dòng tiếp theo, dòng thứ ~i~ chứa xâu ~S_i~ (~1 \leq i \leq n~, ~1 \leq |S_i| \leq 10^5~).
~m~ dòng tiếp theo, dòng thứ ~j~ chứa hai xâu đặc trưng của thao tác trích xuất ~P_j, Q_j~, cách nhau bởi một dấu cách (~1 \leq j \leq m~, ~1 \leq |P_j|, |Q_j| \leq m~).
~\sum |S_i|, \sum |P_j|, \sum |Q_j| \leq 2 \cdot 10^6~.
Output
Xuất ra file ~m~ dòng, dòng thứ ~j~ chứa một số nguyên là kết quả của thao tác trích xuất thứ ~j~.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| ~1~ | ~36 \%~ | ~n, m, \lvert S_i \rvert, \lvert P_j \rvert, \lvert Q_j \rvert \le 100~ |
| ~2~ | ~28 \%~ | ~n, m \le 5 \times 10^3~ |
| ~3~ | ~12 \%~ | ~\sum \lvert S_i \rvert, \sum \lvert P_j \rvert, \sum \lvert Q_j \rvert \le 10^5~ |
| ~4~ | ~24 \%~ | Không có giới hạn gì thêm |
Sample Input 1
2 3
AUGC
AGC
G C
AU C
A C
Sample Output 1
0
1
2
Sample Input 2
3 3
AA
AA
AGA
AA AA
AG GA
AG GA
Sample Output 2
2
1
1
Notes
Sample 1:
Thao tác 1: Không có RNA nào bắt đầu bằng G.
Thao tác 2: AU|G|C thỏa mãn
Thao tác 3: Cả hai xâu đều thỏa mãn
Sample 2:
- Thao tác 2: Xâu AGA vẫn thỏa mãn, mặc dù hai xâu P = AG và Q = GA bị chồng lên nhau khi xếp trên xâu ban đầu.
Điểm: 100
Cho tập hợp ~S~ gồm một số các số nguyên dương. Hãy tìm một tập con ~S' \subseteq S~ thoả mãn:
~\forall x, y \in S': x \neq y \Longrightarrow gcd(x, y) = 1~
~|S'|~ là lớn nhất
Input
Nhập vào file COPRIME.INP:
Dòng ~1~: số nguyên dương ~|S|~
Dòng ~2 \rightarrow |S| + 1~: mỗi dòng gồm một số nguyên dương, miêu tả một phần tử trong tập hợp ~S~
Output
Xuất ra file COPRIME.OUT một số nguyên duy nhất là lực lượng lớn nhất của tập con ~S'~ thoả mãn.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~25\%~ | ~maxS \le 20~ |
| 2 | ~45\%~ | ~maxS \le 100~ |
| 3 | ~30\%~ | ~maxS \le 5000~ |
Sample Input 1
5
30
2
15
5
6
Sample Output 1
2
Notes
~S = \{30, 2, 15, 5, 6\}~
~S' = \{5, 6\}~
Điểm: 100
Trong lúc rảnh rỗi, Nam đã thiết kế ra một trò chơi đơn giản để giải trí. Trò chơi được thực hiện trên một bảng có dạng lưới kích thước ~m \times n~, trong đó mỗi ô được tô một trong hai màu đen hoặc trắng. Các hàng trên bảng được đánh số từ ~1~ đến ~m~ từ trên xuống dưới, các cột được đánh số từ ~1~ đến ~n~ từ trái sang phải, ô ở hàng ~i~ cột ~j~ là ô ~(i, j)~.
Nam được phép biến đổi bảng bằng cách sử dụng thao tác sau:
Chọn một hình vuông kích thước ~2 \times 2~ trên bảng;
Đảo màu tất cả các ô ở trong hình vuông đó (các ô màu đen trong hình vuông sẽ trở thành màu trắng và các ô màu trắng trong hình vuông sẽ trở thành màu đen).
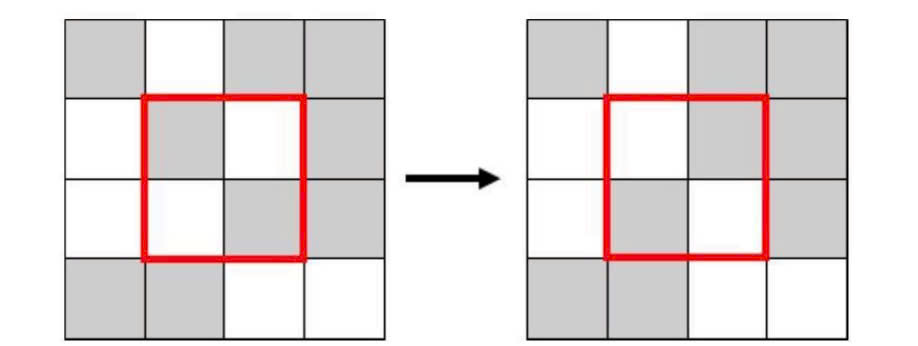
Sau nhiều ngày thử nghiệm, Nam đã tìm ra bảng yêu thích của cậu ấy. Tuy nhiên Nam lại không ghi lại cách để tạo ra bảng đó nên giờ cậu ấy không thể tạo ra bảng yêu thích của mình.
Yêu cầu: Bạn được cho bảng hiện tại của Nam. Hãy giúp Nam biến đổi bảng để tạo ra bảng yêu thích của cậu ấy sau không quá 10 000 thao tác.
Input
Vào từ file văn bản BOARD.INP:
Dòng đầu tiên chứa hai số nguyên ~m~ và ~n~ cách nhau bởi dấu cách là kích thước của bảng ~(2 \leq m, n \leq 100)~;
~m~ dòng tiếp theo mô tả bảng hiện tại của Nam, dòng thứ ~i~ chứa một xâu ~n~ kí tự, trong đó kí tự thứ ~j~ bằng W nếu ô ~(i, j)~ trong bảng hiện tại có màu trắng, ngược lại kí tự thứ ~j~ bằng B nếu ô ~(i, j)~ trong bảng hiện tại có màu đen;
~m~ dòng cuối cùng mô tả bảng yêu thích của Nam, dòng thứ ~i~ chứa một xâu ~n~ kí tự, trong đó kí tự thứ ~j~ bằng W nếu ô ~(i, j)~ trong bảng yêu thích có màu trắng, ngược lại kí tự thứ ~j~ bằng B nếu ô ~(i, j)~ trong bảng yêu thích có màu đen.
Output
Ghi ra file văn bản BOARD.OUT:
Dòng đầu tiên in ra YES nếu có thể biến đổi thành bảng yêu thích của Nam, hoặc NO trong trường hợp ngược lại.
Nếu có thể biến đổi được thì:
Dòng thứ hai in ra một số nguyên ~k~ là số thao tác để biến đổi bảng ban đầu thành bảng yêu thích của Nam (~0 \leq k \leq 10 000~);
~k~ dòng cuối cùng in ra dãy thao tác biến đổi, dòng thứ ~i~ in ra hai số nguyên ~x~ và ~y~ với ô ~(x, y)~ tương ứng là góc trái trên của hình vuông ~2 \times 2~ được chọn trong thao tác thứ ~i~ ~(1 \leq x < m, 1 \leq y < n)~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~50\%~ | Tồn tại cách biến đổi gồm không quá ~1~ thao tác |
| 2 | ~30\%~ | ~m = 2~ |
| 3 | ~20\%~ | Không có ràng buộc gì thêm |
Sample Input 1
2 2
BW
WB
WB
BW
Sample Output 1
YES
1
1 1
Sample Input 2
2 3
BWB
WBW
BBB
WWW
Sample Output 2
NO
Sample Input 3
3 3
WWW
BWW
WWB
WBB
WWB
BBB
Sample Output 3
YES
2
1 2
2 1
Notes
Trong test ví dụ đầu tiên, có thể biến đổi sau ~1~ thao tác như sau:
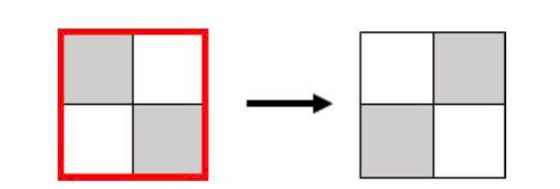
Trong test ví dụ thứ hai, không thể biến đổi được:
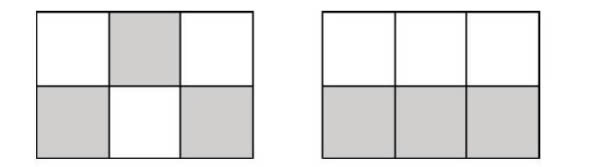
Trong test ví dụ thứ ba, có thể biến đổi sau ~2~ thao tác như sau:
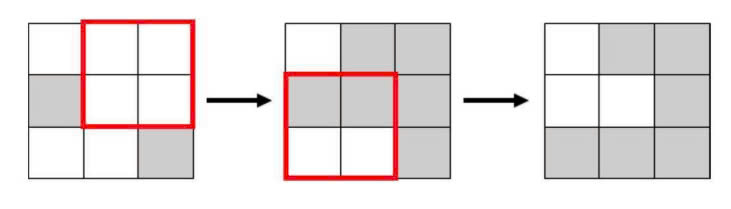
Điểm: 100
Leo núi là môn thể thao trong đó người tham gia leo lên, xuống hoặc băng qua các vách đá tự nhiên hoặc các bức tường đá nhân tạo. Mục tiêu là đạt đến đỉnh của một địa hình hoặc điểm cuối của tuyến đường được xác định trước mà không bị ngã.
Đây là môn thể thao đòi hỏi người chơi cần có sự kiên nhẫn, cơ thể khỏe mạnh, sức bền, sự dẻo dai, bộ môn thể thao này chính là một thử thách lớn dành cho những ai luôn muốn chiến thắng bản thân và ưa thích sự mạo hiểm.
Nam là một người rất thích leo núi, cậu dự định sẽ luyện tập ở một dãy núi gồm ~n~ ngọn núi. Các ngọn núi được đánh số từ ~1~ đến ~n~, từ trái sang phải, ngọn núi thứ ~i~ có độ cao ~h_i~. Để đảm bảo buổi leo núi được thú vị và an toàn, cậu sẽ chọn ra một số ngọn núi thỏa mãn đồng thời các quy tắc sau:
Leo các ngọn núi đã chọn theo thứ tự tăng dần chỉ số;
Bắt đầu ở một ngọn núi thấp để làm quen với địa hình, sau đó leo lên một ngọn núi cao hơn (nếu có);
Nếu ngọn núi đang leo cao hơn ngọn núi đã leo ngay trước đó, ngọn núi tiếp theo cần thấp hơn ngọn núi đang leo (nếu có);
Nếu ngọn núi đang leo thấp hơn ngọn núi đã leo ngay trước đó, ngọn núi tiếp theo cần cao hơn ngọn núi đang leo (nếu có);
Ngọn núi được chọn leo cuối cùng cần thấp hơn ngọn núi đã leo ngay trước đó (nếu có).
Nói cách khác, giả sử các ngọn núi được chọn là ~a_1, a_2, ..., a_k~ thì cần thỏa mãn đồng thời các điều kiện sau:
~k~ là một số nguyên dương lẻ;
~1 \le a_1 < a_2 < ... < a_k \le n~;
~h_{a_1} < h_{a_2} > h_{a_3} < ... > h_{a_k}~.
Do điều kiện thời tiết thất thường, một số ngọn núi có thể không leo được nên Nam đã vạch ra ~q~ giả định. Mỗi giả định gồm hai số nguyên ~l, r~ giả định rằng chỉ có các ngọn núi có chỉ số từ ~l~ đến ~r~ là có thể leo được.
Yêu cầu: Với mỗi giả định, hãy cho Nam biết số lượng ngọn núi nhiều nhất có thể leo được sao cho vẫn tuân thủ các quy tắc đã đặt ra.
Input
Vào từ file văn bản CLIMBING.INP:
Dòng đầu tiên chứa hai số nguyên ~n~ và ~q~, lần lượt là số ngọn núi và số giả định (~1 \le n, q \le 2 \times 10^5~);
Dòng thứ hai chứa ~n~ số nguyên mô tả dãy núi, số thứ ~i~ là ~h_i~, độ cao của ngọn núi thứ ~i~ (~1 \le h_i \le 10^9~);
~q~ dòng cuối cùng, mỗi dòng chứa hai số nguyên ~l, r~ mô tả một giả định (~1 \le l, r \le n~).
Output
Ghi ra file văn bản CLIMBING.OUT:
- Gồm ~q~ dòng, dòng thứ ~i~ in ra một số nguyên là số lượng ngọn núi nhiều nhất có thể leo được sao cho vẫn tuân thủ các quy tắc đã đặt ra trong giả định thứ ~i~, theo thứ tự xuất hiện trong dữ liệu.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| ~1~ | ~30 \%~ | ~n, q \le 100~ và ~1 \le h_i \le 2~ |
| ~2~ | ~20 \%~ | ~n, q \le 100~ |
| ~3~ | ~20 \%~ | ~n, q \le 2000~ |
| ~4~ | ~20 \%~ | ~1 \le h_i \le 2~ |
| ~5~ | ~10 \%~ | Không có ràng buộc gì thêm |
Sample Input 1
7 3
1 9 6 10 2 3 5
1 5
3 6
4 7
Sample Output 1
5
3
1
Sample Input 2
6 2
2 1 2 2 1 1
1 3
2 6
Sample Output 2
1
3
Notes
Trong giả định đầu tiên, chọn leo các ngọn núi ~1, 2, 3, 4, 5~.
Trong giả định thứ hai, chọn leo các ngọn núi ~3, 4, 6~.
Trong giả định thứ ba, chọn leo ngọn núi ~4~.
Điểm: 100
Có một mê cung dưới lòng đất gồm ~n~ căn phòng được kết nối với nhau bằng ~n - 1~ đường hầm. Các phòng có dạng hình tròn và được đánh số từ ~1~ đến ~n~. Các đường hầm nối giữa các phòng thỏa mãn các điều kiện sau:
Mỗi đường hầm nối trực tiếp giữa hai phòng khác nhau;
Mọi căn phòng đều có thể đi được đến tất cả các phòng còn lại thông qua các đường hầm.
Nam đang tham gia trò chơi khám phá mê cung trên. Tuy nhiên, khó khăn khi khám phá mê cung là tất cả đèn sẽ được tắt và trong quá trình khám phá người chơi không được mang theo đèn, vì vậy Nam không thể biết được mình đang ở đâu. Để hỗ trợ cho người chơi, mỗi căn phòng đều được lắp đặt một đèn laser đặt ở trung tâm căn phòng. Ban đầu, tất cả các đèn laser đều chỉ đến một đường hầm nào đó. Người chơi sẽ xuất phát ở căn phòng ~1~.
Với trí thông minh của mình, Nam đã nghĩ ra chiến lược khám phá để luôn đảm bảo đi hết được tất cả các phòng như sau:
Khi đến một phòng bất kì (kể cả phòng đầu tiên), xoay đèn laser theo chiều kim đồng hồ cho đến khi nó lại chỉ vào một đường hầm nào đó;
Đi theo hướng của đèn laser vào đường hầm tương ứng;
Lặp lại quá trình trên vô tận.
Để đánh giá độ hiệu quả của chiến lược trên, Nam đưa ra ~q~ câu hỏi. Mỗi câu hỏi gồm một số nguyên ~k~. Nam cần biết chỉ số của căn phòng sau khi Nam đi qua đúng ~k~ đường hầm theo chiến lược trên.
Yêu cầu: Hãy giúp Nam trả lời tất cả các câu hỏi đặt ra.
Input
Vào từ file văn bản MAZE.INP:
Dòng đầu tiên chứa hai số nguyên ~n~ và ~q~ lần lượt là số căn phòng và số câu hỏi của Nam (~2 \le n \le 10^5~, ~1 \le q \le 10^5~);
~n~ dòng tiếp theo mô tả mê cung, dòng thứ ~i~ mô tả căn phòng thứ ~i~. Cụ thể, dòng thứ ~i~ chứa một số nguyên ~d~, theo sau đó là ~d~ số nguyên ~c_1, c_2, \ldots, c_d~, cho biết phòng thứ ~i~ được kết nối với ~d~ đường hầm và các căn phòng chúng dẫn đến, theo chiều kim đồng hồ. Ban đầu, đèn laser ở phòng ~i~ chỉ đến đường hầm dẫn đến phòng ~c_1~;
~q~ dòng cuối cùng mỗi dòng chứa một số nguyên ~k~ mô tả một câu hỏi (~1 \le k \le 10^{12}~).
Các số trên cùng một dòng cách nhau bởi một dấu cách.
Output
Ghi ra file văn bản MAZE.OUT:
- Gồm ~q~ dòng, dòng thứ ~i~ chứa một số nguyên duy nhất là đáp án cho câu hỏi thứ ~i~, theo thứ tự xuất hiện trong dữ liệu.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~20\%~ | ~n, q \le 100~ và ~k \le 100~ trong tất cả câu hỏi |
| 2 | ~20\%~ | ~k \le 10^5~ trong tất cả câu hỏi |
| 3 | ~20\%~ | ~n, q \le 1000~ và tồn tại một đường hầm nối hai phòng ~i~ và ~i + 1~ với mọi ~1 \le i \lt n~ |
| 4 | ~20\%~ | ~n, q \le 1000~ |
| 5 | ~20\%~ | không có ràng buộc gì thêm |
Sample Input 1
5 6
1 3
2 4 3
3 5 1 2
1 2
1 3
1
2
3
4
5
6
Sample Output 1
3
1
3
2
3
5
Notes
Trạng thái ban đầu của mê cung như sau:
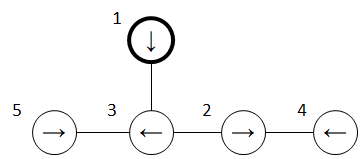
Ban đầu người chơi ở phòng ~1~, thực hiện xoay đèn laser theo chiều kim đồng hồ, đèn laser chỉ vào đường hầm dẫn đến phòng ~3~;
Tại phòng ~3~, xoay đèn laser chỉ vào đường hầm dẫn đến phòng ~1~;
Tại phòng ~1~, xoay đèn laser chỉ vào đường hầm dẫn đến phòng ~3~;
Tại phòng ~3~, xoay đèn laser chỉ vào đường hầm dẫn đến phòng ~2~;
Tại phòng ~2~, xoay đèn laser chỉ vào đường hầm dẫn đến phòng ~3~;
Tại phòng ~3~, xoay đèn laser chỉ vào đường hầm dẫn đến phòng ~5~;