Educational Prefix Sum & Differential Array Contest - Part 2
Cho dãy số nguyên a1, a2, ..., an (~1 \leq n \leq 100000~), mỗi số không vượt quá 10000. Dãy số này được viết trên một vòng tròn. Nghĩa là, khi cắt vòng tròn tại vị trí j, ta thu được:
~a_{j}~, ~a_{j+1}~,..., ~a_{n}~, ~a_1~, ~a_2~, ..., ~a_{j-1}~
Vị trí j được gọi là vị trí tốt, nếu các điều kiện sau đây được thỏa mãn:
- ~a_{j}~ ~>~ 0
- ~a_{j}~ + ~a_{j+1}~ ~>~ 0
- ....
- ~a_{j}~ + ~a_{j+1}~ + ... + ~a_{n}~ ~>~ 0
- ~a_{j}~ + ~a_{j+1}~ + ... + ~a_{n}~ + ~a_1~ ~>~ 0
- ...
- ~a_{j}~ + ~a_{j+1}~ + ... + ~a_{n}~ + ~a_1~ + ~a_2~ + ... + ~a_{j─2}~ ~>~ 0
- ~a_{j}~ + ~a_{j+1}~ + ... + ~a_{n}~ + ~a_1~ + ~a_2~ + ... + ~a_{j─2}~ + ~a_{j─1}~ ~>~ 0
Yêu cầu: hãy đếm số vị trí tốt.
Input
- Dòng đầu tiên chứa số nguyên n.
- Dòng thứ 2 chứa dãy số ~a_1~, ~a_2~,...,~a_{n}~.
Output
- In ra 1 số nguyên duy nhất là số vị trí tốt.
Sample Input
5
0 1 -2 10 3
Sample Output
2
Điểm: 100
Trong trường hợp đề bài hiển thị không chính xác, bạn có thể tải đề bài tại đây: Đề bài
Bạn được cho một dãy ~a~ gồm các số nguyên từ ~0~ tới ~9~. Một dãy ~a~ được gọi là tốt khi và chỉ khi tổng của dãy đó bằng số phần tử của dãy đó (~\sum_{i=l}^{r} a_i = r - l + 1~).
Ví dụ, với dãy ~a = [1, 2, 0]~, có ~3~ dãy tốt: ~[1]~, ~[2, 0]~, ~[1, 2, 0]~.
Hãy đếm số dãy con liên tiếp là dãy tốt trong dãy ~a~.
Input
Dòng đầu tiên chứa số nguyên dương ~t~ (~1 \le t \le 1000~) là số lượng test.
Dòng đầu tiên của mỗi test gồm số nguyên dương ~n~ (~1 \le n \le 10^5~) là số phần tử của dãy ~a~.
Dòng thứ hai của mỗi test gồm ~n~ chữ số được viết liền nhau, là các phần tử trong dãy.
Dữ liệu đảm bảo tổng của ~n~ qua mọi test không vượt quá ~10^5~.
Output
Với mỗi test in ra một số nguyên, là số dãy con liên tiếp là dãy tốt trong dãy ~a~.
Sample Input 1
2
5
12321
4
1023
Sample Output 1
2
3
Notes
Trong test đầu tiên, có hai dãy tốt là ~[1, 1]~ và ~[5, 5]~.
Trong test thứ hai, có ba dãy tốt là ~[1, 1]~, ~[1, 3]~ và ~[2, 3]~.
Điểm: 100
Trong trường hợp đề bài hiển thị không chính xác, bạn có thể tải đề bài tại đây: Đề bài
Lưu ý: các bạn không nhập, xuất dữ liệu bằng file kể cả khi đề bài có yêu cầu. Đọc, ghi dữ liệu được thực hiện ở stdin và stdout.
Điểm: 100
Cho một khối lập phương kích thước ~n~ chia làm ~n^{3}~ khối lập phương đơn vị. Mỗi khối lập phương đơn vị chứa ~1~ số nguyên.
Bạn hãy tìm một khối lập phương con của khối lập phương đã cho sao cho tổng các số trong khối lập phương con đó là lớn nhất.
Input
- Dòng đầu: số lượng test.
- Tiếp theo là các test, mỗi test gồm: dòng đầu là ~n~. Sau đó ~n~ nhóm dòng thể hiện lớp cắt của hình lập phương nhìn từ mặt trước từ gần ra xa, mỗi nhóm gồm ~n~ dòng, mỗi dòng gồm ~n~ số liệt kê các số trên lớp cắt từ trên xuống dưới, trái qua phải.
Chú ý: ~n \leq 30~. Giá trị của khối lập phương đơn vị thuộc kiểu integer.
Output
- Mỗi dòng chứa tổng của khối lập phương con lớn nhất của test tương ứng.
Sample Input
2
3
0 -1 3
-5 7 4
-8 9 1
-1 -3 -1
2 -1 5
0 -1 3
3 1 -1
1 3 2
1 -2 1
4
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
Sample Output
27
64
Điểm: 100
Sau khi đi lang thang, Alice bị lạc vào 1 công viên kì lạ, chứa ~n~ tấm bạt lò xo được xếp thành ~1~ hàng. Tấm bạt lò xo thứ ~i~ có độ nảy là ~S_i~.
Alice có thể nhảy trên các tấm bạt lò xo nhiều lần. Cô bắt đầu một lượt nhảy bằng cách nhảy lên bất kì tấm bạt lò xo nào mà mình chọn.
Nếu Alice nhảy lên tấm bạt lò xo thứ ~i~, cô sẽ bay đến vị trí ~i + S_i~ và độ nảy của tấm bạt lò xo thứ ~i~ sẽ bị hao hụt đi ~1~. Vì các tấm bạt lò xo luôn có độ nảy dù ít hay nhiều, nên ~S_i~ luôn lớn hơn hoặc bằng ~1~ trong mọi thời điểm. Nói cách khác, khi Alice nhảy lên tấm bạt lò xo thứ ~i~, thì ~S_i = max(S_i - 1, 1)~. Nếu không có tấm bạt lò xò nào ở vị trí ~i + S_i~, thì lượt nhảy hoàn thành. Ngược lại, Alice sẽ tiếp tục lượt bằng cách nhảy khỏi tấm bạt ở vị trí ~i + S_i~, theo nguyên tắc được mô tả ở trên.
Alice không thể kết thúc lượt cho đến khi cô ấy đáp ở vị trí lớn hơn ~n~. Với tính cách nghịch ngợm của mình, cô cảm thấy phấn khích với điều đó. Cô muốn phá hủy công viên lò xo bằng cách giảm độ nảy của toàn bộ ~n~ tấm bạt xuống ~1~. Vì không giỏi tính toán, Alice muốn hỏi bạn liệu cô ấy cần ít nhất bao nhiêu lượt nhảy để có thể phá hủy được công viên. Hãy giúp Alice nhé!
Input
Dòng đầu tiên chứa số nguyên dương ~n~ (~1 \le n \le 10^6~) — độ dài của công viên.
Dòng thứ hai gồm ~n~ số nguyên dương ~S_1, S_2, \ldots, S_n~ (~1 \le S_i \le 10^9~) — độ nảy của ~n~ tấm bạt lò xo.
Output
Ghi ra trên một dòng là số lượt ít nhất Alice cần phải nhảy.
Sample Input 1
7
1 4 2 2 2 2 2
Sample Output 1
4
Notes
Trình tự nhảy tối ưu được thể hiện bên dưới (vị trí các tấm bạt lò xo mà Alice nhảy lên trong mỗi lượt được in đậm)
[1, 4, 2, 2, 2, 2, 2]
[1, 3, 2, 2, 2, 1, 2]
[1, 2, 2, 2, 1, 1, 1]
[1, 1, 2, 1, 1, 1, 1]
Điểm: 100
Cho bảng 2 chiều gồm ~N~ dòng và ~M~ cột, trong đó ~A_{ij}~ nhận một trong hai giá trị là # hoặc .. Trả lời các truy vấn dạng ~(U, L, D, R, K)~ dạng:
Đếm số điểm ~(i,j)~ sao cho hình vuông con ~K \times K~ có góc trái trên là ~(i,j)~ nằm trọn trong hình chữ nhật con có góc trái trên là ~(U,L)~, và góc phải dưới là ~(D,R)~, và hình vuông con này chỉ chứa toàn dấu '.'. Nói cách khác, ta cần đếm số điểm ~(i,j)~ thoả mãn đồng thời:
~U \le i \le i+K-1 \le D~,
~L \le j \le j+K-1 \le R~,
~A_{uv} =~ '.' ~\forall u \in [i, i+K-1], v \in [j, j+K-1]~.
Input
Dòng đầu tiên chứa ba số nguyên dương ~N~, ~M~ và ~Q~ thể hiện kích thước của bảng và số truy vấn (~1 \le N,M \le 2000~, ~1 \le Q \le 3 \cdot 10^5~).
~N~ dòng tiếp theo, mỗi dòng chứa một xâu kí tự độ dài ~M~. Dữ liệu vào đảm bảo mỗi kí tự trong xâu chỉ nhận một trong hai giá trị là # hoặc ..
~Q~ dòng cuối cùng, mỗi dòng chứa 5 số nguyên ~U~ ~L~ ~D~ ~R~ ~K~ thể hiện một truy vấn (~1 \le U \le D \le N~, ~1 \le L \le R \le M~, ~1 \le K \le 10~).
Output
Với mỗi truy vấn, in ra kết quả của truy vấn đó trên một dòng.
Sample Input 1
5 5 4
..#.#
.....
#....
...#.
.#...
1 1 3 3 2
3 3 5 5 2
2 1 3 4 2
1 1 5 5 2
Sample Output 1
2
0
2
5
Sample Input 2
4 4 4
....
....
....
...#
1 1 4 4 1
1 1 4 4 2
1 1 4 4 3
2 2 4 3 2
Sample Output 2
15
8
3
2
Notes
Xét test ví dụ đầu tiên:
Các ô thoả mãn ở truy vấn ~1~: (~1~, ~1~), (~2~, ~2~)
Các ô thoả mãn ở truy vấn ~3~: (~2~, ~2~), (~2~, ~3~)
Các ô thoả mãn ở truy vấn ~4~: (~1~, ~1~), (~2~, ~2~), (~2~, ~3~), (~2~, ~4~), (~3~, ~2~)
Điểm: 100
Cô bé An rất thích những bài toán liên quan đến truy vấn mảng.
Một ngày nọ, cô gặp một bài toán khá nổi tiếng: bạn có một mảng gồm ~n~ phần tử (các phần tử được đánh số từ ~1~). Ngoài ra, có ~q~ truy vấn; mỗi truy vấn được mô tả bởi một cặp số nguyên ~l_i, r_i~ ~(1 \le l_i \le r_i \le n)~.
Với mỗi truy vấn, bạn cần tìm tổng các phần tử của mảng trong đoạn chỉ số từ ~l_i~ đến ~r_i~ (bao gồm cả hai đầu).
Tuy nhiên, cô bé cảm thấy bài toán này hơi nhàm chán. Cô quyết định thay đổi thứ tự các phần tử trong mảng trước khi trả lời các truy vấn sao cho tổng của tất cả các kết quả truy vấn là lớn nhất có thể.
Nhiệm vụ của bạn là tính giá trị lớn nhất có thể của tổng các kết quả truy vấn sau khi sắp xếp lại mảng một cách tối ưu.
Input
Dòng đầu tiên chứa hai số nguyên ~n~ và ~q~ ~(1 \le n \le 2 \cdot 10^5, \ 1 \le q \le 2 \cdot 10^5)~ — số phần tử của mảng và số truy vấn.
Dòng tiếp theo chứa ~n~ số nguyên ~a_i~ ~(1 \le a_i \le 2 \cdot 10^5)~ — các phần tử của mảng.
Mỗi dòng trong ~q~ dòng tiếp theo chứa hai số nguyên ~l_i, r_i~ ~(1 \le l_i \le r_i \le n)~ — truy vấn thứ ~i~.
Output
In ra một số nguyên duy nhất — tổng lớn nhất có thể của tất cả các truy vấn sau khi sắp xếp lại mảng tối ưu.
Scoring
Sample Input 1
3 3
5 3 2
1 2
2 3
1 3
Sample Output 1
25
Sample Input 2
5 3
5 2 4 1 3
1 5
2 3
2 3
Sample Output 2
33
Notes
Với Test đầu tiên
Ta có thể sắp xếp lại mảng thành ~[2,5,3]~
Khi đó, truy vấn đầu tiên sẽ cho ra kết quả là ~2+5=7~.
Truy vấn thứ hai cho ra kết quả là ~5+3=8~.
Truy vấn thứ ba cho ra kết quả là ~2+5+3=10~.
Kết quả sẽ bằng ~7+8+10=25~.
Có thể chứng minh được là không có phương án nào khác cho ra kết quả lớn hơn.
Điểm: 100
Cho một dãy số nguyên ~a_1, a_2, \cdots, a_n~ gồm ~n~ phần tử và một số nguyên ~m~. Bạn cần xử lý ~q~ truy vấn, trong đó mỗi truy vấn thuộc một trong hai loại sau:
~1~ ~l~ ~r~ ~val~: với mỗi chỉ số ~i~ thoả mãn ~l \le i \le r~, thực hiện gán ~a_i = (a_i + val) \mod m~.
~2~ ~l~ ~r~: kiểm tra xem trong đoạn con ~a_l, a_{l + 1}, \cdots, a_r~ có tồn tại ít nhất hai giá trị khác nhau hay không.
Với từng truy vấn loại ~2~, nếu có, in ra ~\text{YES}~, ngược lại in ra ~\text{NO}~ nếu tất cả các phần tử trong đoạn đều bằng nhau.
Input
Dòng đầu chứa ba số nguyên ~n, q~ và ~m~ (~1 \le n, q \le 2 \times 10^5~, ~m \le 10^9~);
Dòng thứ hai chứa ~n~ số nguyên ~a_1, a_2, \cdots, a_n~ (~0 \le a_i < m~);
Trong ~q~ dòng cuối cùng, mỗi dòng mô tả một truy vấn thuộc một trong hai loại trên (~1 \le l \le r \le n~, ~0 \le val < m~).
Output
Với mỗi truy vấn loại 2, in ra trên một dòng chứa kết quả tương ứng là ~\text{YES}~ hoặc ~\text{NO}~.
Scoring
Sample Input 1
5 5 10
1 2 3 4 5
2 1 3
1 2 4 8
2 1 3
1 2 3 1
2 1 2
Sample Output 1
YES
YES
NO
Notes
Truy vấn 1 tồn tại hai giá trị khác nhau (1, 3) : 1 và 2
Sau truy vấn 2, dãy thay đổi thành [1, 0, 1, 2, 5]
Sau truy vấn 4, dãy thay đổi thành [1, 1, 2, 2, 5]
Truy vấn cuối cùng (1,2) không có hai giá trị nào khác nhau
Điểm: 100
Cho mảng ~a~ gồm ~n~ phần tử, ban đầu có giá trị bằng ~1~. Thực hiện hai loại truy vấn:
~1~ ~l~ ~r~ ~x~: tăng đoạn ~[l, r]~ lên ~x~ đơn vị (~1 \le l \le r \le n~, ~1 \le x \le 10^9~).
~2~ ~l~ ~r~: tìm ~\gcd (a_l, a_{l + 1}, ..., a_r)~ (~1 \le l \le r \le n~).
Input
Dòng đầu tiên chứa hai số nguyên dương ~n~ và ~q~ (~1 \le n, q \le 2 \times 10^5~), thể hiện số phần tử của mảng ~a~ và số truy vấn.
~q~ dòng tiếp theo, mỗi dòng chứa một truy vấn thuộc một trong hai loại trên.
Output
Với mỗi truy vấn loại ~2~, ghi ra trên một dòng kết quả của truy vấn đó.
Sample Input 1
5 5
2 1 5
1 2 3 5
1 4 5 2
2 2 4
2 2 3
Sample Output 1
1
3
6
Notes
Ban đầu, ~a = [1,1,1,1,1]~
Sau hai truy vấn thêm, ~a=[1,6,6,3,3]~
Một mảnh giấy hình chữ nhật được chia thành ~n~ hàng và ~m~ cột. Trong đó, đã có ~f~ ô được điền sẵn giá trị ~1~, các ô còn lại được điền giá trị ~0~. Bạn cần tìm một hình vuông kích thước ~k \times k~ thoả mãn:
~k~ chia hết cho ~d~,
Tồn tại một ô ~(i,j)~ sao cho hình vuông kích thước ~k \times k~ có góc trái trên là ~(i,j)~ chứa ~\le c~ ô có giá trị ~1~,
~k~ lớn nhất.
Input
Dòng đầu tiên chứa 5 số nguyên dương ~n~, ~m~, ~f~, ~d~, ~c~ (~1 \le n,m \le 5000~, ~1 \le f \le 2 \cdot 10^5~, ~1 \le d \le \min(m,n)~, ~1 \le c \le nm~).
~f~ dòng tiếp theo, mỗi dòng chứa hai số nguyên ~i~, ~j~ thể hiện một ô được điền giá trị ~1~ (~1 \le i \le n~, ~1 \le j \le m~).
Output
Gồm một dòng duy nhất chứa số nguyên dương ~k~ thoả mãn yêu cầu.
Sample Input 1
5 5 9 1 1
2 2
3 5
1 5
4 5
5 2
1 1
1 2
4 2
2 5
Sample Output 1
2
Notes
Giải thích: Ta chọn hình vuông có góc trái trên là ~(1,3)~, với độ dài cạnh là ~2~.
Điểm: 100
Cho một mảng ~A~ gồm ~N~ phần tử và ~Q~ truy vấn. Mỗi truy vấn cho ~4~ tham số ~l,r,v,k~. Với mỗi truy vấn ta phải làm thao tác sau: $$\forall i\in [l,r] :a_i=(a_i+v*k^{i-l} )\%(10^9+7)$$ Hãy in ra mảng ~A~ sau ~Q~ truy vấn.
Input
Dòng đầu gồm ~2~ số nguyên ~N,Q(1\le N,Q\le2*10^5)~
~Q~ dòng tiếp theo, mỗi dòng gồm ~4~ số ~l,r,v,k(1\le l\le r\le n,1\le v\le 10^9,1\le k\le 200)~
Output
- Gồm ~N~ số là giá trị của mảng ~A~ sau ~Q~ truy vấn.
Sample Input 1
5 3
2 3 7 7
3 5 2 13
1 5 6 9
Sample Output 1
6 61 537 4400 39704
Notes
Sau truy vấn thứ nhất, các phần tử trong dãy ~A~ lần lượt bằng ~0,7,49,0,0~.
Sau truy vấn thứ hai, các phần tử trong dãy ~A~ lần lượt bằng ~0,7,51,26,338~.
Sau truy vấn thứ ba, các phần tử trong dãy ~A~ lần lượt bằng ~6,61,537,4400,39704~.
Điểm: 100
Cho bảng hai chiều kích thước ~n\times m~, với ô ~(i,j)~ có giá trị là ~a_{i,j}~. Nhiệm vụ của bạn là chọn ra ba hình vuông kích thước ~k\times k~ không giao nhau sao cho tổng giá trị của các ô thuộc ít nhất một hình vuông là lớn nhất.
Input
Dòng đầu tiên gồm ba số nguyên dương ~n,m,k~ tương ứng với kích thước của bảng và kích thước của mỗi hình vuông ~(1\le n,m\le 1500, 1\le k\le min(n,m))~. Dữ liệu đảm bảo có thể chọn ra ba hình vuông kích thước ~k\times k~ không giao nhau trên bảng.
Dòng thứ ~i~ trong ~n~ dòng tiếp theo gồm ~m~ số nguyên ~a_{i,1},a_{i,2},\dots,a_{i,m}~ tương ứng với giá trị của các ô trên bảng ~(0\le a_{i,j}\le 500)~.
Output
In ra duy nhất một số nguyên là tổng giá trị tối đa có thể đạt được.
Sample Input 1
9 9 3
1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1
1 8 8 8 8 8 1 1 1
1 8 8 8 8 8 1 1 1
1 8 8 8 8 8 1 1 1
1 1 1 1 8 8 8 1 1
1 1 1 1 1 1 8 8 8
1 1 1 1 1 1 9 9 9
1 1 1 1 1 1 9 9 9
Sample Output 1
208
Notes
Phương án tối ưu cho test ví dụ được mô tả ở hình phía dưới (các ô màu xanh lá tương ứng với các ô được bao phủ bởi ít nhất một hình vuông).
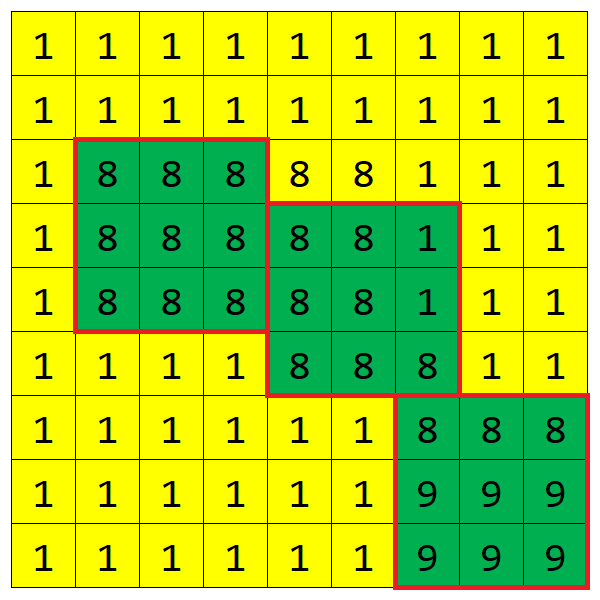
Điểm: 100
Ông Bảo là chủ của một trang trại, đang nuôi một đàn bò trên khu đất hình chữ nhật chia thành lưới ~m \times n~ ô vuông đơn vị. Các hàng của lưới được đánh số từ ~1~ tới ~m~ từ trên xuống, và các cột của lưới được đánh số từ ~1~ tới ~n~ từ trái qua phải. Ô nằm trên giao điểm của hàng ~i~ và cột ~j~ được gọi là ô ~(i,\: j)~. Tại tâm của một số ô đã cắm cọc, mỗi cọc để buộc một con bò. Để bảo vệ đàn bò tót quý của mình khỏi những tên trộm, ông Bảo thuê Hùng tìm một thửa đất có dạng hình thoi (mà theo quan niệm của ông Bảo là biểu tượng cho may mắn) trong khu đất để nhốt đàn bò của mình. Thửa đất hình thoi có tâm tại ô ~(x_0,\: y_0)~ và bán kính là ~r~ là tập hợp tất cả các ô có tọa độ ~(x, \:y)~ thỏa mãn ~|x - x_0| + |y - y_0| \leq r~. Do bò tót là các con vật rất hung dữ, nên ông Bảo yêu cầu trong thửa đất tìm được không có hai ô có cọc nào lại có cạnh chung.
Yêu cầu: Giúp Hùng xác định thửa đất có dạng hình thoi nằm trọng vẹn trong khu đất với số cọc cột bò là nhiều nhất đáp ứng yêu cầu của ông Bảo.
Input
- Dòng đầu tiên chứa ~2~ số nguyên ~m~ và ~n~ xác định kích thước của khu đất của ông Bảo.
- Dòng thứ ~i~ trong ~m~ dòng sau chứa ~n~ kí tự liền nhau, mỗi kí tự xác định trạng thái của một thửa đất: '*' nếu ô đất có cắm cọc và '.' nếu ô đất đó không cắm cọc.
Output
Đưa ra ~4~ số nguyên ~S, \:x_0,\: y_0, \:r~ được ghi cách nhau một dấu cách, trong đó: ~S~ là tổng số cọc trong thửa đất được chọn; ~x_0,\: y_0~ là tọa độ tâm và ~r~ là bán kính của thửa đất đó. Nếu có nhiều lời giải hãy đưa ra một lời giải bất kỳ.
Giới hạn
- Có ~40~% số test ứng với ~40~% số điểm của bài có ~1 \leq m,\:n \leq 100.~
- Có ~40~% số test khác ứng với ~40~% số điểm của bài có ~1 \leq m,\:n \leq 500.~
- Có ~20~% số test còn lại ứng với ~20~% số điểm của bài có ~1 \leq m, \:n \leq 1000.~
Sample Input 1
2 3
...
..*
Sample Output 1
1 2 3 0
Sample Input 2
3 3
*.*
...
*.*
Sample Output 2
1 1 1 0
Sample Input 3
3 3
.*.
*.*
.*.
Sample Output 3
4 2 2 1