Educational Prefix Sum & Differential Array Contest - Part 1
Điểm: 100
Cho một dãy số gồm ~n~ phần tử nguyên ~a_1, a_2, \cdots, a_n~ và bạn phải trả lời ~q~ truy vấn, mỗi truy vấn có dạng hai số ~(l, r)~ yêu cầu tính tổng ~a_l~ ~+~ ~a_{l + 1}~ ~+~ ~\cdots~ ~+~ ~a_r~.
Input
Dòng đầu tiên chứa hai số nguyên ~n~ và ~q~ (~1 \le n, q \le 10^5~) — số phần tử và số truy vấn.
Dòng thứ hai chứa ~n~ số nguyên ~a_1, a_2, \cdots, a_n~ (~-10^9 \le a_i \le 10^9~) — dãy ~a~.
Trong ~q~ dòng tiếp theo, mỗi dòng gồm hai số ~l_i~ và ~r_i~ (~1 \le l_i \le r_i \le n~) — truy vấn thứ ~i~.
Output
In ra ~q~ dòng là đáp án cho ~q~ truy vấn.
Sample Input 1
5 3
1 3 -2 3 4
2 3
1 4
3 5
Sample Output 1
1
5
5
Notes
Trong các truy vấn:
Truy vấn ~1~: ~a_2 + a_3 = 3 - 2 = 1~;
Truy vấn ~2~: ~a_1 + a_2 + a_3 + a_4 = 1 + 3 - 2 + 3 = 5~;
Truy vấn ~3~: ~a_3 + a_4 + a_5 = -2 + 3 + 4 = 5~.
Điểm: 100
Cho một hình chữ nhật có ~N~ hàng và ~M~ cột, các hàng được đánh số từ ~1~ đến ~N~ từ trên xuống dưới, các cột được đánh số từ ~1~ đến ~M~ từ trái sang phải. Mỗi ô (~i, j~) chứa một số nguyên ~A_{i,j}~.
Cho ~Q~ truy vấn, mỗi truy vấn gồm ~4~ số nguyên ~x_1, y_1, x_2, y_2~ mô tả một hình chữ nhật con có góc trái trên là ô (~x_1, y_1~) và góc phải dưới là ô (~x_2, y_2~). Với mỗi truy vấn, hãy in ra tổng của các số trong hình chữ nhật con đó.
Input
Dòng đầu tiên chứa ~3~ số nguyên ~N, M, Q~ (~1 \leq N, M \leq 1000; 1 \leq Q \leq 10^5~) — lần lượt là kích thước của hình chữ nhật và số truy vấn.
~N~ dòng tiếp theo, mỗi dòng chứa ~M~ số nguyên, giá trị tuyệt đối của mỗi số không quá ~10^9~.
~Q~ dòng cuối cùng, mỗi dòng chứa ~4~ số nguyên ~x_1, y_1, x_2, y_2~ (~1 \leq x_1, x_2 \leq N; 1 \leq y_1, y_2 \leq M~) mô tả một hình chữ nhật cần truy vấn.
Output
Gồm ~Q~ dòng, mỗi dòng in tổng các số nằm trong hình chữ nhật tương ứng.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~40~ | ~N,M,Q \le 100~ |
| 2 | ~60~ | Không có ràng buộc gì thêm |
Sample Input 1
4 5 3
-4 9 1 2 -3
3 2 3 -2 -4
7 -1 -1 2 1
5 3 -4 -8 2
2 3 2 5
2 1 4 5
1 1 2 2
Sample Output 1
-3
8
10
Sample Input 2
3 3 2
9 1 -4
2 -3 -3
-1 -2 5
2 2 3 3
3 1 3 2
Sample Output 2
-3
-3
Điểm: 100
Cho một dãy ~A~ gồm ~n~ phần tử ~A_1, A_2, \ldots, A_n~. Tìm dãy con liên tiếp có tổng lớn nhất của ~A~.
Dãy con liên tiếp của ~A~ là đoạn liên tục, gồm các phần tử nằm liền nhau của ~A~. Ví dụ cho dãy ~A = [6, -1, 2, 8, -4]~ thì dãy ~B = [-1, 2, 8]~ là một dãy con liên tiếp của dãy ~A~. Còn dãy ~C = [6, 2, -4]~ không là một dãy con liên tiếp của ~A~.
Input
Dòng đầu tiên chứa số nguyên dương ~n~ (~1 \le n \le 10^5~) — độ dài dãy ~A~.
Dòng thứ hai gồm ~n~ số nguyên mô tả dãy ~A~ (~|A_i| \le 10^9~).
Output
Gồm một dòng duy nhất chứa giá trị dãy con liên tiếp có tổng lớn nhất của dãy ~A~.
Sample Input 1
6
-1 3 -1 2 1 -5
Sample Output 1
5
Notes
Dãy con liên tiếp có tổng lớn nhất là ~A_2 + A_3 + A_4 + A_5 = 3 - 1 + 2 + 1 = 5~
Điểm: 100
Cho mảng ~A~ gồm ~n~ số nguyên. Nhiệm vụ của bạn là đếm số lượng cặp chỉ số ~(l,r)\ (1\le l\le r\le n)~ sao cho trung bình cộng giá trị của các phần tử ~A_l,A_{l+1},\dots,A_r~ bằng ~K~.
Input
Dòng đầu tiên gồm hai số nguyên ~n,K~ tương ứng với số lượng phần tử và giá trị trung bình cộng ~K~ ~(1\le n\le 10^5,|K|\le 10^6)~.
Dòng thứ hai gồm ~n~ số nguyên ~A_1,A_2,\dots,A_n~ tương ứng với các phần tử trong dãy ~(|A_i|\le 10^6)~.
Output
In ra duy nhất một giá trị là số lượng cặp số thỏa mãn.
Sample Input 1
5 1
-3 2 -4 1 5
Sample Output 1
2
Notes
Có hai cặp số thỏa mãn là ~(2,5)~ và ~(4,4)~.
Điểm: 100
Cho mảng ~a~ gồm ~n~ phần tử. Hãy tìm hai đoạn con liên tiếp, không giao nhau, khác rỗng của mảng ~a~, sao cho tổng của hai đoạn con đó là lớn nhất.
Nói cách khác, hãy tìm ra bộ bốn chỉ số ~i, j, u, v~ (~1 \le i \le j < u \le v \le n~), sao cho tổng ~a[i...j] + a[u...v]~ là lớn nhất.
Input
Dòng đầu tiên chứa số nguyên dương ~n~ (~2 \le n \le 3 \times 10^5~) là số phần tử của mảng.
Dòng thứ hai gồm ~n~ số nguyên ~a_i~ (~0 \le |a_i| \le 10^9~) là các phần tử của mảng.
Output
Tổng lớn nhất của hai đoạn con không giao nhau, khác rỗng.
Sample Input 1
5
3 -2 5 -3 4
Sample Output 1
10
Notes
Để đạt tổng lớn nhất là ~10~, ta chọn đoạn con ~[1, 3]~ và đoạn con ~[5, 5]~. Đây là hai đoạn con có tổng dương lớn nhất, không giao nhau, nên kết quả ~6 + 4 = 10~ là tối ưu.
Điểm: 100
Cho một mảng ~a~ gồm ~n~ phần tử và một số nguyên dương ~D~. Nhiệm vụ của bạn là đếm số đoạn con liên tiếp của ~a~ mà có tổng các phần tử trong đoạn chia hết cho ~D~.
Input
Dòng đầu tiên gồm hai số nguyên dương ~n~ và ~D~ tương ứng với số phần tử của mảng ~a~ và hằng số ~D\ (1\le n,D\le 10^5)~.
Dòng thứ hai gồm ~n~ số nguyên ~a_1,a_2,\dots,a_n~ tương ứng với các phần tử trong mảng ~a\ (|a_i|\le 10^9)~.
Output
Gồm duy nhất một giá trị là số đoạn con thỏa mãn.
Sample Input 1
5 4
1 3 -2 3 -5
Sample Output 1
4
Notes
Có bốn đoạn con thỏa mãn điều kiện của đề bài:
Đoạn con ~[1;2]~ do ~a_1+a_2=1+3=4~ chia hết cho ~4~.
Đoạn con ~[1;5]~ do ~a_1+a_2+a_3+a_4+a_5=1+3-2+3-5=0~ chia hết cho ~4~.
Đoạn con ~[2;4]~ do ~a_2+a_3+a_4=3-2+3=4~ chia hết cho ~4~.
Đoạn con ~[3;5]~ do ~a_3+a_4+a_5=-2+3-5=-4~ chia hết cho ~4~.
Điểm: 100
Cho bảng hai chiều kích thước ~n\times m~, với ô ~(i,j)~ có giá trị là ~a_{i,j}~. Nhiệm vụ của bạn là chọn ra một bảng con sao cho tổng giá trị của các ô trên đó là lớn nhất.
Input
Dòng đầu tiên gồm hai số nguyên dương ~n,m~ tương ứng với kích thước của bảng ~(1\le n,m\le 500)~.
Dòng thứ ~i~ trong ~n~ dòng tiếp theo gồm ~m~ số nguyên ~a_{i,1},a_{i,2},\dots,a_{i,m}~ tương ứng với giá trị của các ô trên bảng ~(|a_{i,j}|\le 10^9)~.
Output
In ra duy nhất một số nguyên là tổng giá trị tối đa có thể đạt được.
Sample Input 1
2 3
1 -4 3
2 2 -3
Sample Output 1
4
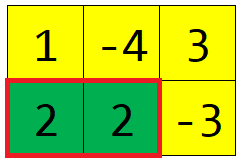
Notes
Phương án tối ưu cho test ví dụ được mô tả ở hình phía dưới (các ô màu xanh lá tương ứng với các ô nằm trên bảng con được chọn).
Điểm: 100
Sau khi thoát ra khỏi công viên lò xo, Alice lại bị cuốn vào một vùng đất huyền bí, nơi có rất nhiều viên ngọc nằm vương vãi khắp nơi.
Vùng đất được mô tả bằng một lưới có kích thước ~N \times N~ ô vuông. Ô ở dòng ~i~ và cột ~j~ (~1 \le i, j \le N~) có ~P(i, j)~ viên ngọc (~0 \le P(i, j) \le 10^9~). Từ vị trí đứng của Alice, cô chỉ có thể đi không quá ~K~ bước. Mỗi bước đi chỉ được phép đi theo ~1~ trong ~4~ hướng lên, xuống, sang trái hoặc sang phải.
Hãy giúp Alice chọn vị trí đứng tối ưu sao cho cô có thể lấy được nhiều viên ngọc nhất trước khi rời khỏi vùng đất này.
Input
Dòng đầu tiên gồm ~2~ số nguyên ~N, K~ (~1 \le N \le 1000~, ~0 \le K \le 2 \times N~) — lần thước là kích thước của vùng đất và số bước tối đa Alice có thể đi.
~N~ dòng tiếp theo, mỗi dòng chứa ~N~ số nguyên mô tả vùng đất.
Output
Gồm ~1~ dòng duy nhất chứa số viên ngọc tối đa mà Alice có thể lấy được.
Sample Input 1
5 2
77 64 56 33 28
0 80 67 34 75
1 93 66 92 77
12 36 4 63 22
21 47 84 99 45
Sample Output 1
753
Notes
Alice sẽ đứng ở vị trí ~(3, 3)~ và lấy được những viên ngọc nằm ở các ô được in đậm như mô tả ở dưới:
$$\begin{array}{rrrrr} 77 & 64 & \textbf{56} & 33 & 28 \\ 0 & \textbf{80} & \textbf{67} & \textbf{34} & 75 \\ \textbf{1} & \textbf{93} & \textbf{66} & \textbf{92} & \textbf{77} \\ 12 & \textbf{36} & \textbf{4} & \textbf{63} & 22 \\ 21 & 47 & \textbf{84} & 99 & 45 \end{array}$$
Một vụ tai nạn giao thông vừa xảy ra ngoài phố. Mọi người tò mò chen lấn vòng trong vòng ngoài để xem. Rất đông người xem vụ tai nạn như: khanhcank7, nhungngoisao, chicuong123, harryporter7, mr_ntt, manhboyak6. Một anh đến chậm không tài nào vào xem được. Tức quá, anh ta liền hét toáng lên:
- Tôi là bố kẻ bị nạn đây!
Mọi người kinh ngạc quay lại nhìn và vội vã giãn ra cho anh ta vào. "Kẻ bị nạn" là một... chú chó vừa bị xe cán chết.
Ngại ngùng, anh ta chạy về nhà, than khóc. Và ông tiên hellosirius hiện ra ban cho anh ta 1 điều ước. Anh ta ước rằng mọi người trên thế giới sẽ quên hết mọi chuyện trong hôm nay. Tuy nhiên, theo định luật bảo toàn năng lượng cũng như định luật bảo toàn tính mạng ông tiên buộc chú phải giải bài toán sau mới giúp chú thực hiện điều ước. Nhanh chóng chú giải được bài toán ông đưa ra tuy nhiên, lần này ông buộc chú phải chiến đấu với hiệp sĩ đẹp trai n_cqt và blackstar . Để chiến thắng hiệp sĩ cách duy nhất là giải được bài toán hiệp sĩ đưa ra ( vì hiệp sĩ không những đẹp trai, học giỏi mà còn khỏe mạnh vô đối nữa ). Đề bài của hiệp sĩ như sau:
Cho dãy số nguyên ~A~ gồm ~N~ phần tử ~A_{1}~ ,~A_{2}~ ,...,~A_{n}~ . Tìm cặp chỉ số ~i,j~ thỏa mãn:
DSEQ ~= |(A_{1} + A_{2} + \dots + A_{i}) - (A_{j} + A_{j+1} + \dots + A_{n})|~ đạt giá trị lớn nhất (với ~1 \leq i < j \leq N)~.
Hãy giúp anh bạn khốn khổ của chúng ta hoàn thành điều ước!
Input
Dòng đầu là số nguyên dương ~N~; ~(2 \leq N \leq 10^{6})~.
Dòng tiếp theo chứa ~N~ số nguyên ~A_{1}~, ~A_{2}~, ..., ~A_{n}~; ~(|A_{i}|< 10^{9})~, các số cách nhau một dấu cách.
Output
Gồm một dòng chứa 2 số nguyên là DSEQ lớn nhất tìm được (do hiệp sĩ n_cqt yêu cầu) và số cặp chỉ số thỏa mãn (hai số cách nhau một dấu cách) (do hiệp sĩ blackstar yêu cầu)
Giới hạn
~\frac{1}{2}~ số test có ~N \leq 5000~
Sample Input
5
1 -2 3 -4 -7
Sample Output
13 1
Điểm: 100
Cho mảng ~a~ gồm ~n~ phần tử. Có ~q~ truy vấn, mỗi truy vấn gồm ba tham số ~l~, ~r~ và ~x~ với ý nghĩa: tăng đoạn con liên tiếp từ ~l~ tới ~r~ trong mảng lên ~x~ đơn vị.
Yêu cầu: In ra mảng sau ~q~ truy vấn.
Input
Dòng đầu tiên ghi hai số nguyên dương ~n~ và ~q~ (~1 \le n, q \le 2 \times 10^5~), là số phần tử của mảng ~a~ và số truy vấn.
Dòng thứ hai ghi ~n~ số nguyên dương ~a_i~ (~1 \le a_i \le 10^9~), là giá trị ban đầu của mảng.
~q~ dòng tiếp theo, mỗi dòng chứa ba số nguyên dương ~l~, ~r~, ~x~ (~1 \le l \le r \le n~, ~1 \le x \le 10^9~) mô tả từng truy vấn.
Output
Mảng sau ~q~ truy vấn.
Sample Input 1
5 3
1 3 8 2 1
1 3 2
1 4 2
5 5 1
Sample Output 1
5 7 12 4 2
Notes
Sau truy vấn 1, mảng là ~[3, 5, 10, 2, 1]~.
Sau truy vấn 2, mảng là ~[5, 7, 12, 4, 1]~.
Sau truy vấn 3, mảng là ~[5, 7, 12, 4, 2]~.
Điểm: 100
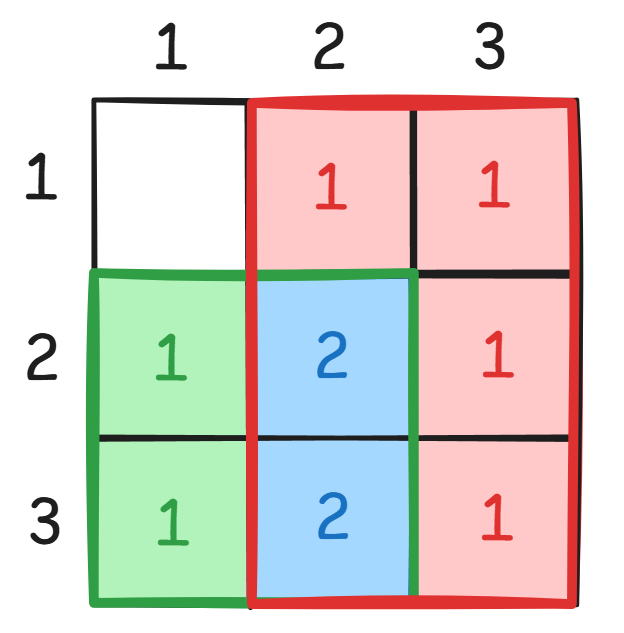
Cho mảng ~2~ chiều ~a~ gồm ~n~ hàng và ~m~ cột chỉ chứa các số ~0~. Có ~q~ truy vấn, mỗi truy vấn gồm bốn tham số (~a~, ~b~, ~c~, ~d~) với ý nghĩa: tăng một đơn vị với mỗi ~a_{i, j}~ thoả mãn ~a \le i \le c~ và ~b \le j \le d~.
Yêu cầu: In ra mảng sau ~q~ truy vấn.
Input
Dòng đầu tiên gồm ba số nguyên ~n, m~ và ~q~ (~1 \le n, m \le 1000~, ~1 \le q \le 10^5~);
Trong ~q~ dòng tiếp theo, mỗi dòng gồm bốn số nguyên ~a, b, c, d~ (~1 \le a, c \le n~, ~1 \le b, d \le m~).
Output
In ra mảng sau tất cả truy vấn.
Sample Input 1
3 3 2
1 2 3 3
2 1 3 2
Sample Output 1
0 1 1
1 2 1
1 2 1
Notes
Trong ví dụ trên, có hai truy vấn tăng hai hình chữ nhật màu xanh và đỏ như trong hình vẽ.