Educational DSU Contest Part 2
Điểm: 100
Cho một đồ thị vô hướng liên thông có trọng số, tìm cây khung với trọng số nhỏ nhất.
Input
Dòng đầu tiên gồm hai số nguyên ~n~ và ~m~ (~2 \le n \le 200000, 1 \le m \le 200000~) — lần lượt là số đỉnh và số cạnh
Mỗi dòng trong ~m~ dòng tiếp theo gồm ba số nguyên ~b_i~, ~e_i~ và ~w_i~ (~1 \le b_i~, ~e_i \le n, 0 \le w_i \le 100000~) — lần lượt là cạnh nối thứ ~i~ giữa ~b_i~ và ~e_i~, và trọng số của cạnh thứ ~i~.
Output
Gồm một số nguyên duy nhất là trọng số nhỏ nhất của cây khung.
Sample Input 1
2 1
1 2 2
Sample Output 1
2
Sample Input 2
4 3
3 1 7
1 4 14
2 1 12
Sample Output 2
33
Điểm: 100
Cho một đồ thị vô hướng có ~n~ đỉnh và ~m~ cạnh có trọng số.
Ta định nghĩa giá trị của một cây khung là hiệu trọng số của cạnh có trọng số lớn nhất với cạnh có trọng số bé nhất.
Yêu cầu: Tìm giá trị bé nhất của một cây khung được tạo ra từ đồ thị đã cho.
Nhắc lại kiến thức, một cây khung là một đồ thị liên thông có ~n~ đỉnh và ~n-1~ cạnh có trọng số.
Input
Dòng đầu tiên gồm hai số nguyên dương ~n~ và ~m~ (~2 \leq n \leq 1000~, ~0 \leq m \leq 10000~) — là số đỉnh và số cạnh của đồ thị.
Trong ~m~ dòng tiếp theo, dòng thứ ~i~ gồm ba số nguyên ~u_i~, ~v_i~ và ~w_i~ (~1 \leq u_i, v_i \leq n~, ~|w_i| \leq 10^9~) — là cạnh nối giữa hai đỉnh ~u_i~ với ~v_i~ và có trọng số là ~w_i~.
Output
Gồm một dòng duy nhất là đáp án của yêu cầu đề bài; nếu không tìm được thì hãy in ra "NOT FOUND".
Sample Input 1
3 3
1 2 2
2 3 1
1 3 2
Sample Output 1
0
Sample Input 2
3 1
1 2 2
Sample Output 2
NOT FOUND
Tại đất nước VNOI, có ~n~ thành phố được kết nối với nhau bằng một hệ thống giao thông gồm ~m~ con đường hai chiều có trọng số. Hệ thống này luôn đảm bảo tính liên thông, nghĩa là giữa hai thành phố bất kì luôn có ít nhất một đường đi giữa chúng.
Ở mỗi thành phố luôn có một trạm xăng với vô hạn xăng, nhưng trên đường đi giữa hai thành phố kề nhau lại không có trạm xăng nào, do đó khi dừng chân tại một thành phố, bạn có thể đổ đầy bình xăng của mình. Biết với mỗi lần đi giữa hai thành phố kề nhau, bạn bị mất một lượng xăng là trọng số của con đường đó; hãy tính dung tích nhỏ nhất của bình xăng của xe bạn, mà đảm bảo rằng bạn không bao giờ bị hết xăng khi đang di chuyển trên đường đi giữa hai thành phố bất kì.
Input
Dòng đầu tiên gồm hai số nguyên ~n~ và ~m~ (~2 \le n \le 2 \cdot 10^5~, ~1 \le m \le 4 \cdot 10^5~) — thể hiện số thành phố và số con đường trực tiếp giữa hai thành phố.
Trong ~m~ dòng tiếp theo, dòng thứ ~i~ chứa ba số nguyên ~u_i \ v_i \ d_i~ thể hiện rằng có đường đi trực tiếp giữa ~u_i~ và ~v_i~ với trọng số ~d_i~ (~1 \le u_i,v_i \le n~, ~0 \le d_i \le 10^5)~.
Output
In ra một số nguyên duy nhất là đáp án của bài toán.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~20\%~ | ~1 \le n,m \le 10^3~ |
| 2 | ~10\%~ | ~m=n-1~ |
| 3 | ~70\%~ | Không có ràng buộc gì thêm |
Sample Input 1
3 2
1 2 5
1 3 10
Sample Output 1
10
Sample Input 2
3 3
1 2 5
1 3 10
2 3 5
Sample Output 2
5
Notes
Ví dụ thứ nhất: xe của bạn cần có ít nhất ~10~ đơn vị xăng, để đảm bảo có thể di chuyển từ ~1 \rightarrow 3~ và ~2 \rightarrow 3~ mà không bị hết xăng.
Ví dụ thứ hai: xe của bạn chỉ cần chứa ít nhất ~5~ đơn vị xăng, do mọi đường đi tốt nhất giữa các cặp đỉnh chỉ cần đi qua các cạnh có trọng số ~5~.
NKN99 là một học sinh đang học về môn hóa. Trong môn hóa, bạn đang học về liên kết ion, liên kết cộng hóa trị và liên hết hydro. Để dễ hình dung thì bạn được giáo viên cho phát một mô hình nguyên tử của các chất. Chất bạn đang có trên tay gồm ~N~ nguyên tử và ~M~ liên kết. Bạn ấy khá phá nên bạn ấy muốn bỏ nhiều liên kết nhất để mô hình còn đủ ~N~ phân tử hóa học liên kết với nhau. Dù vậy, mỗi liên kết có một độ khó để loại bỏ khác nhau. Dù vậy, cũng như khá lười, tổng độ khó các cạnh bạn ấy loại bỏ không được quá ~S~. Bạn hãy giúp bạn NKN99 phá mô hình của giáo viên nhé.
Input
Dòng đầu gồm 3 số ~N,M,S(1\le N\le50000,1\le M\le 100000,1\le S\le10^{18})~
~M~ dòng tiếp theo, mỗi dòng gồm ~3~ số là ~U,V,C~ có nghĩa là có liên kết giữa nguyên tử ~U~ và nguyên tử ~V~ với độ khó để loại bỏ là ~C(1\le C\le10^9)~. Mô hình đảm bảo không có hai liên kết nào cùng nối vào một cặp nguyên tố giống nhau và các liên kết ban đầu tạo thành một đồ thị liên thông.
Output
Dòng đầu gồm ~1~ số là số liên kết nhiều nhất có thể loại bỏ.
Dòng thứ hai gồm một vài số là chỉ số cạnh được loại bỏ theo thứ tự tăng dần.
Nếu có nhiều cách in ra cách bất kỳ.
Sample Input 1
6 7 10
1 2 3
1 3 3
2 3 3
3 4 1
4 5 5
5 6 4
4 6 5
Sample Output 1
2
1 6
Sample Input 2
6 10 20
4 3 4
2 4 2
1 4 3
6 3 2
5 1 5
5 2 3
3 5 2
4 6 4
6 5 3
6 2 4
Sample Output 2
5
2 3 4 6 7
Điểm: 100
Đêm giáng sinh đang cận kề, đôi tình nhân Nauq và Hana quyết định mua cho mình một cây thông và trang trí nó. Nauq và Hana mua một bộ đèn gồm ~n~ bóng đèn để nối chúng với nhau và treo lên cây thông. Một bóng đèn có hai chế độ phát sáng là sáng màu xanh lá hoặc sáng màu đỏ. Nauq và Hana cho rằng một cây thông được gọi là thõa mãn tính thẩm mỹ khi hai bóng đèn bất kì được nối với nhau phải khác màu nhau.
Để không khí buổi trang trí cây thông của cả hai thêm vui vẻ, Hana quyết định chơi một trò chơi với Nauq gồm hai thao tác như sau:
Hana chọn ra hai bóng đèn ~x~ và ~y~. Nếu hai bóng đèn này đang được nối trong hai cụm đèn khác nhau, Hana sẽ nối chúng với nhau và thực hiện đổi màu đèn sao cho chúng thỏa mãn tính thẩm mỹ mà cả hai đã đưa ra. Ngược lại, nếu chúng cùng được nối trong một cụm đèn thì Hana không làm gì cả.
Hana đưa ra hai bóng đèn ~x~ và ~y~. Nếu hai bóng đèn này đang được nối trong cùng một cụm đèn, Hana sẽ hỏi Nauq rằng liệu hai bóng đèn này có cùng màu hay không. Ngược lại, nếu hai bóng đèn này không nằm trong cùng một cụm đèn thì Hana sẽ yêu cầu Nauq nói "Merry Christmas!".
Lưu ý: Ban đầu chưa có bóng đèn nào được nối với nhau.
Input
Dòng đầu tiên gồm hai số nguyên dương ~n~ và ~m~ — lần lượt là số bóng đèn và số thao tác mà Hana sẽ chơi với Nauq (~1 \le n, m \le 2 \times 10^5~).
Tiếp theo gồm ~m~ dòng mô tả các thao tác của Hana có dạng như sau:
Thao tác loại một: "~1~ ~x~ ~y~" (~1 \le x, y \le n~).
Thao tác loại hai: "~2~ ~x~ ~y~" (~1 \le x, y \le n~).
Output
In ra mỗi dòng là "Yes", "No" lần lượt ứng mỗi mỗi thao tác loại hai nếu hai bóng đèn được hỏi có cùng màu hay không. Nếu thao tác loại hai này Hana hỏi Nauq hai bóng đèn mà không được nối trong cùng một cụm đèn thì in ra "Merry Christmas!".
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| ~1~ | ~30 \%~ | ~n, m \le 5000~ |
| ~2~ | ~30 \%~ | Mọi thao tác loại một đều được thực hiện trước mọi thao tác loại hai |
| ~3~ | ~40 \%~ | Không có ràng buộc gì thêm |
Sample Input 1
3 4
1 1 2
1 2 3
2 1 2
2 1 3
Sample Output 1
No
Yes
Sample Input 2
6 8
1 1 4
2 1 4
1 1 2
2 2 4
1 2 5
1 4 6
2 1 5
2 1 6
Sample Output 2
No
Yes
Yes
Yes
Sample Input 3
3 2
1 1 2
2 1 3
Sample Output 3
Merry Christmas!
Notes
Giải thích test ví dụ thứ nhất: Sau hai thao tác đầu tiên, các bóng đèn được nối lần lượt theo thứ tự là ~1~ - ~2~ - ~3~. Do đó, ta có thể có hai cách bật đèn là đỏ - xanh - đỏ hoặc xanh - đỏ - xanh ứng với các đèn ~1~ - ~2~ - ~3~.
Giải thích test ví dụ thứ ba: Trong thao tác thứ hai, bóng đèn ~1~ và bóng đèn ~3~ không nằm trong một cụm đèn trước đó nên Nauq cần nói "Merry Christmas!"
Điểm: 100
Một đồ thị được gọi là hai phía khi có thể chia tập đỉnh thành hai phần sao cho không có cạnh nào nối hai đỉnh thuộc cùng một phần.
Trong bài toán này, ~m~ cạnh sẽ lần lượt được thêm vào một đồ thị rỗng (đồ thị không có cạnh) gồm ~n~ đỉnh.
Yêu cầu: Hãy xác định chỉ số của cạnh đầu tiên mà sau khi thêm cạnh đó vào, đồ thị không còn giữ được tính hai phía nữa.
Input
Dòng đầu tiên gồm hai số nguyên ~n~ mà ~m~ ~(1 \le n, m \le 3 \cdot 10^5)~— số đỉnh ban đầu và số cạnh sẽ được thêm vào trong đồ thị.
~m~ dòng tiếp theo, mỗi dòng gồm 2 số nguyên ~u_i~ và ~v_i~ ~(1 \le u_i, v_i \le n)~, cho biết cạnh được thêm vào thứ ~i~ sẽ nối hai đỉnh ~u_i~ và ~v_i~. Đề bài đảm bảo đồ thị không tồn tại khuyên hoặc đa cạnh tại mọi thời điểm.
Output
- In ra một số nguyên duy nhất là chỉ số của cạnh đầu tiên (các cạnh được đánh số từ ~1~ theo thứ tự xuất hiện trong đầu vào), hoặc -1, nếu không tồn tại cạnh nào như vậy.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| ~1~ | ~30\%~ | ~1 \le n, m \le 3\,000~ |
| ~2~ | ~70\%~ | Không có ràng buộc gì thêm |
Sample Input 1
4 4
1 2
2 3
1 3
2 4
Sample Output 1
3
Sample Input 2
6 4
1 2
2 3
3 4
1 4
Sample Output 2
-1
Notes
Ở ví dụ đầu tiên, sau khi thêm cạnh thứ ~3~, đồ thị gồm các cạnh ~(1, 2)~, ~(1, 3)~ và ~(2, 3)~ không còn giữ được tính chất của đồ thị hai phía. Vậy đáp án là ~3~.
Ở ví dụ thứ hai, sau khi thêm tất cả các cạnh, đồ thị vẫn là đồ thị hai phía.
Điểm: 100
Trong bài toán này, chúng ta cần cài đặt DSU Rollback cơ bản.
Cho ~N~ tập, tập thứ ~i~ hiện tại đang chứa số ~i~.
Chúng ta có ~Q~ truy vấn thuộc một trong ba loại.
"~union~ ~u~ ~v~" — gộp 2 tập chứa số ~u~ và ~v~, và in ra số tập hiện tại.
"~persist~" — tạo ra một checkpoint để lúc sau chúng ta có thể quay lại.
"~rollback~" — đưa các tập về trạng thái ở checkpoint gần nhất, xóa checkpoint đó, và in ra số tập hiện tại.
Input
Dòng đầu tiên chứa số ~N~ ~(N \leq 2 \times 10^5)~ và ~Q~ ~(Q \leq 2 \times 10^5)~ lần lượt là số tập và số truy vấn.
~Q~ dòng tiếp theo bao gồm các truy vấn gồm một trong ba loại (ý nghĩa của từng loại truy vấn như trên):
~union~ ~u~ ~v~ ~(1 \le u, v \le N, u < v)~
~persist~
~rollback~
Output
Với mỗi truy vấn loại ~union~ hoặc ~rollback~, in ra đáp án tương ứng.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~25~ | ~N, Q \le 3000~ |
| 2 | ~75~ | Không có điều kiện gì thêm |
Sample Input 1
5 10
persist
union 1 2
union 3 4
persist
union 1 4
union 2 3
rollback
union 4 5
rollback
union 1 5
Sample Output 1
4
3
2
2
3
2
5
4
Sample Input 2
4 10
persist
union 1 2
union 2 3
persist
union 1 3
persist
union 1 4
rollback
rollback
rollback
Sample Output 2
3
2
2
1
2
2
4
Notes
Giải thích test đề ~1~:
Đầu tiên, ta đặt checkpoint đầu tiên (nếu lúc sau ta có rollback về checkpoint này, ta sẽ phải xóa đi tất cả những cạnh trước đây)
Sau đó, ta gộp các tập ~(1, 2)~ và ~(3, 4)~. Khi đó chúng ta còn lại lần lượt ~4~ và ~3~ tập.
Ta tiếp tục đặt thêm ~1~ checkpoint.
Ta gộp các tập chứa ~1~ và ~4~. Khi đó ta còn ~2~ tập — ~1~ tập chứa ~{1, 2, 3, 4}~ và tập còn lại chứa ~5~.
Ta gộp tập chứa ~2~ và ~3~, tuy nhiên do ~2~ và ~3~ thuộc cùng ~1~ tập nên truy vấn này không làm thay đổi số tập.
Ta rollback, tức quay lại trạng thái trước checkpoint thứ ~2~, và xóa đi checkpoint này. Khi đó ta có ~2~ tập lần lượt là ~{1, 2, 5}~ và ~{3, 4}~
Ta tiếp tục rollback về lại checkpoint đầu tiên, và xóa đi tất cả các lần gộp từ đầu tới giờ. Do đó ta quay trở về với ~5~ tập.
Ta gộp ~2~ tập ~{1, 5}~ và khi đó chúng ta có ~4~ tập.
Cho đơn đồ thị vô hướng gồm ~n~ đỉnh và ~m~ cạnh ảo, tức ban đầu đồ thị chưa có cạnh.
Có ~k~ vũ trụ song song khác nhau, vũ trụ song song thứ ~i~ (~1 \leq i \leq k~) được biểu diễn bởi cặp số ~l_i, r_i~ (~l_i \leq r_i~): tất cả cạnh có chỉ số từ ~l_i~ đến ~r_i~ sẽ biến thành cạnh thật, tức sẽ có ~r_i - l_i + 1~ cạnh tồn tại trên đồ thị. Các vũ trụ song song không có khả năng tác động đến nhau.
Với mỗi vũ trụ song song, đếm số lượng thành phần liên thông trên đồ thị.
Input
Dòng đầu gồm hai số nguyên ~n, m~ (~1 \leq n, m \leq 50000~).
~m~ dòng tiếp theo, dòng thứ ~i~ chứa hai số nguyên ~u_i, v_i~ biểu diễn một cạnh vô hướng của đồ thị (~1 \leq u_i, v_i \leq n~, ~u_i \neq v_i~).
Dòng tiếp theo chứa số nguyên ~k~ (~1 \leq k \leq 50000~).
Dòng thứ ~i~ trong ~k~ dòng tiếp theo chứa hai số nguyên ~l_i, r_i~ (~1 \leq l_i \leq r_i \leq m~) biểu diễn một vũ trụ song song.
Output
Xuất ra ~k~ dòng, dòng thứ ~i~ là đáp án cho vũ trụ song song thứ ~i~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~20\%~ | ~n, m, k \leq 2000~. |
| 2 | ~30\%~ | ~l_i \leq 10~ (~1 \leq i \leq k~) và ~r_i \leq r_{i+1}~ (~1 \leq i \leq k-1~). |
| 3 | ~50\%~ | Không có ràng buộc gì thêm. |
Sample Input 1
3 3
1 2
2 3
1 3
5
1 1
1 2
2 3
3 3
1 3
Sample Output 1
2
1
1
2
1
Sample Input 2
8 6
1 2
2 3
3 1
3 4
4 5
5 3
7
3 5
1 6
1 4
3 6
2 4
2 3
5 6
Sample Output 2
5
4
5
5
5
6
6
Notes
Trong test ví dụ thứ hai, đồ thị "ảo" nhìn như sau:
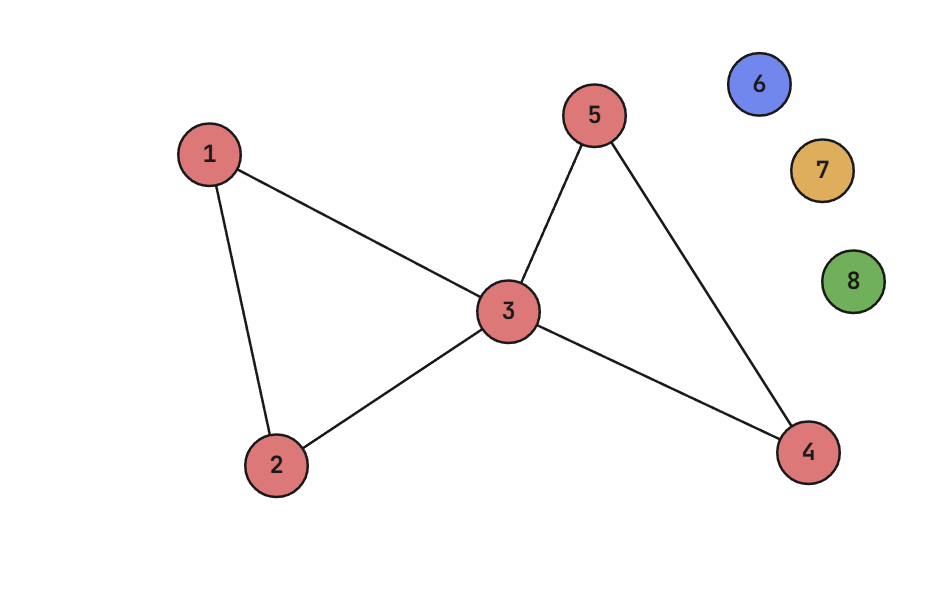
Đồ thị "thật" trong vũ trụ song song đầu tiên nhìn như sau, đồ thị được tô ~5~ màu tương ứng với ~5~ thành phần liên thông:
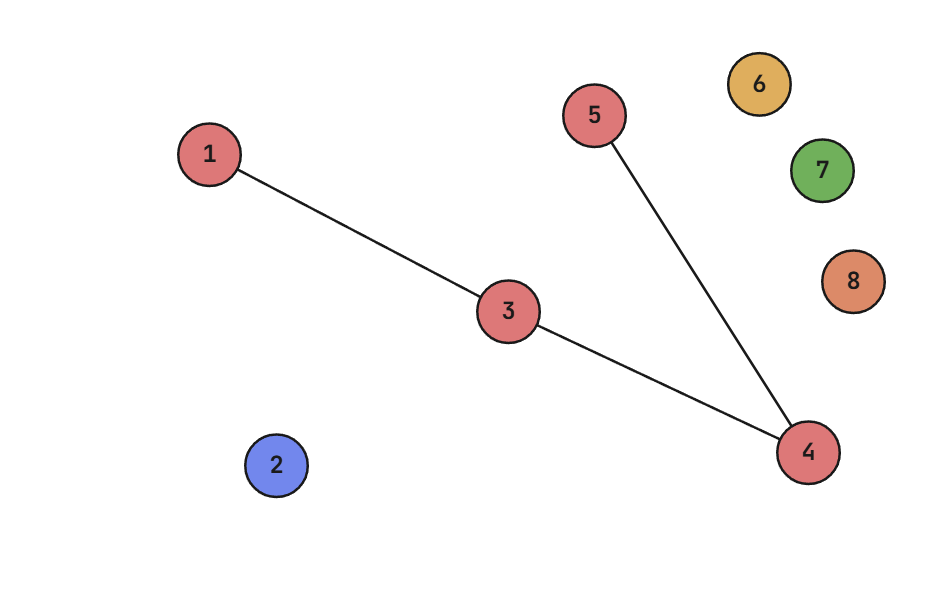
Điểm: 100
Bạn được cho một đồ thị vô hướng rỗng với ~n~ đỉnh. Bạn cần trả lời các truy vấn của ba loại sau:
"~+~ ~u~ ~v~" — thêm một cạnh vô hướng ~u - v~ vào đồ thị.
"~-~ ~u~ ~v~" — xóa một cạnh vô hướng ~u - v~ khỏi đồ thị.
"~?~" — tính số lượng thành phần liên thông trong đồ thị.
Input
Dòng đầu tiên gồm hai số nguyên ~n~ và ~m~ ~(1 \le n \le 3 \cdot 10^5, 0 \le m \le 3 \cdot 10^5)~ — số lượng đỉnh và số lượng truy vấn.
~m~ dòng tiếp theo mô tả các truy vấn thuộc một trong ba loại sau:
~+~ ~u~ ~v~ ~(1 \le u \neq v \le n)~. Đảm bảo rằng đồ thị không có cạnh ~u - v~ trước đó.
~-~ ~u~ ~v~ ~(1 \le u \neq v \le n)~. Đảm bảo rằng đồ thị có cạnh ~u - v~ trước đó.
~?~
Output
Với mỗi truy vấn ~?~, in ra số lượng thành phần liên thông trong đồ thị tại thời điểm truy vấn đó, mỗi kết quả in ra trên một dòng riêng biệt.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~30~ | ~n, m \le 5000~ |
| 2 | ~70~ | Không có ràng buộc gì thêm |
Sample Input 1
5 11
?
+ 1 2
+ 2 3
+ 3 4
+ 4 5
+ 5 1
?
- 2 3
?
- 4 5
?
Sample Output 1
5
1
1
2
Sample Input 2
11 16
?
+ 2 8
+ 9 10
+ 5 6
+ 4 11
- 4 11
+ 8 11
?
?
- 5 6
- 8 11
- 9 10
+ 6 11
- 2 8
?
+ 10 11
Sample Output 2
11
7
7
10
Notes
Giải thích bộ test đầu tiên:
Ban đầu các thành phần liên thông là (1); (2); (3); (4); (5)
Sau truy vấn thứ hai, các thành phân liên thông là (1, 2); (3); (4); (5)
Sau truy vấn thứ ba, các thành phần liên thông là (1, 2, 3); (4); (5)
~\dots~