[Mirror] Code Tour 2024 - Final Round
Điểm: 500
Cho dãy gồm ~n~ số nguyên dương ~a_1, a_2, \ldots, a_n~. Ban dãy ~a~ thỏa mãn điều kiện ~a_1 \le 2\cdot a_i~ với mọi ~2 \le i \le n~. Đây được gọi là điều kiện cân bằng của dãy ~a~.
Được phép thực hiện dãy các tác sau không hoặc nhiều lần:
Chọn chỉ số ~i~ (~2 \le i \le n~) và số nguyên ~x~ sao cho ~x \le a_i~.
Thực hiện biến đổi ~a_1 \gets a_1 + x~ và ~a_i \gets a_i - x~.
Sau phép biến đổi, điều kiện cân bằng của mảng ~a~ phải được thỏa mãn.
~x~ được gọi là điểm số cho thao tác này.
Tìm tổng điểm số lớn nhất có thể sau khi thực hiện thao tác trên không hoặc nhiều lần.
Input
Bộ dữ liệu gồm nhiều test case. Dòng đầu tiên của bộ dữ liệu chứa số nguyên dương ~t~ (~1 \le t \le 100~) là số lượng test case. Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa số nguyên ~n~ (~2 \le n \le 200\,000~) — độ dài dãy ~a~.
Dòng thứ hai gồm ~n~ số nguyên ~a_1, a_2, \ldots, a_n~ (~1 \le a_i \le 10^9~, ~a_1 \le 2 a_i~ với mọi ~2 \le i \le n~).
Dữ liệu đảm bảo rằng tổng ~n~ trong tất cả các test case không quá ~2 \cdot 10^5~.
Output
Với mỗi test case, hãy in ra tổng điểm số tối đa có thể đạt được sau khi thực hiện thao tác không hoặc vài lần.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~250~ | ~n \le 100~, ~a_i \le 100~ |
| 2 | ~250~ | Không có ràng buộc gì thêm |
| Tổng | ~500~ |
Sample Input 1
3
3
2 3 4
2
1 11
4
5 3 3 3
Sample Output 1
2
7
0
Notes
Với testcase thứ nhất, tổng điểm số tối đa có thể đạt được là ~2~:
ta có ~x = 1~ điểm khi chọn ~i = 2~. Lúc này ta có dãy ~a = [3, 2, 4]~
ta có ~x = 1~ điểm khi chọn ~i = 3~. Lúc này ta có dãy ~a = [4, 2, 3]~.
Với testcase thứ hai, tổng số điểm ta có thể đạt được là ~7~ bằng cách chuyển ~x = 7~ điểm từ vị trí ~i = 2~. Ta thu được dãy ~a = [8, 4]~.
Ở test case thứ ba, ta không có cách tăng điểm nào để thỏa mãn điều kiện cân bằng của dãy ~a~.
Điểm: 1000
Một trong những yếu tố quan trọng giúp VNG vươn lên trong top 5 doanh nghiệp có môi trường làm việc tốt nhất Việt Nam năm 2023 chính là tinh thần đoàn kết mạnh mẽ giữa các nhân viên. Chính nhờ tinh thần này mà mọi công việc nhóm trong công ty đều được hoàn thành không chỉ nhanh chóng mà còn đạt chất lượng vượt trội. Đặc biệt, đối với các nhân viên mới, nhất là các lập trình viên trẻ, VNG không ngừng tổ chức những khóa huấn luyện về tinh thần đồng đội và kỹ năng làm việc nhóm. Hãy cùng khám phá một trò chơi rèn luyện đầy thú vị mà VNG đã tổ chức dưới đây.
Ban đầu, tất cả mọi nhân viên tham gia trò chơi đều được chia vào các nhóm. Có ~2^k~ nhóm, nhóm thứ ~i~ có ~a_i~ nhân viên. Trò chơi cũng có một quản trò sẽ ra các hiệu lệnh. Sau mỗi hiệu lệnh, số lượng nhóm và số lượng thành viên trong các nhóm sẽ thay đổi. Trò chơi sẽ kết thúc khi người quản trò đọc xong tất cả các câu lệnh.
Giả sử ở thời điểm hiện tại đang có ~2^x~ nhóm, nhóm thứ ~i~ đang có ~a'_i~ nhân viên. Hiệu lệnh mà người quản trò sẽ ra thuộc một trong hai loại sau:
Hiệu lệnh 0: Đây là hiệu lệnh gộp nhóm, sẽ có 2 nhóm được gộp lại thành một nhóm lớn hơn. Quá trình gộp nhóm diễn ra như sau:
Nhóm ~2^{x-1}~ sẽ gộp vào nhóm ~1~, tạo ra nhóm có ~a_1 + a_{2^{x-1}}~ nhân viên;
Nhóm ~2^{x-1} + 1~ sẽ gộp vào nhóm ~2~, tạo ra nhóm có ~a_2 + a_{2^{x-1} + 1}~ nhân viên;
...
Nhóm ~2^x~ sẽ gộp vào nhóm ~2^{x-1} - 1~, tạo ra nhóm có ~a_{2^{x-1} - 1} + a_{2^x}~ nhân viên.
Số lượng nhóm giảm xuống còn ~2^{x-1}~, và các nhóm được đánh số từ ~1~ đến ~2^{x-1}~ theo thứ tự vừa mô tả.
Người quản trò đảm bảo rằng tại thời điểm này đang có ít nhất 2 đội.
Hiệu lệnh 1: Đây là hiệu lệnh tách nhóm, mỗi nhóm sẽ được tách thành 2 nhóm nhỏ. Số lượng nhóm sẽ tăng lên thành ~2^{x+1}~, các nhóm sẽ được đánh số từ ~1~ đến ~2^{x+1}~. Trong quá trình này, mỗi nhân viên ở nhóm ~i~ có thể chọn ở lại nhóm thứ ~i~, hoặc di chuyển đến nhóm thứ ~i + 2^x~. Sau thao tác này, một số nhóm có thể không chứa thành viên nào cả.
Giả sử khi trò chơi kết thúc, số nhóm mà mọi người được chia vào sẽ là ~2^h~, nhóm thứ ~i~ sẽ có ~b_i~ nhân viên. Nhiệm vụ của tất cả mọi người tham gia trò chơi là khi trò chơi kết thúc, dãy ~b~ được tạo thành cần phải là dãy có thứ tự từ điển nhỏ nhất có thể tạo được trong tất cả các dãy có thể được tạo ra.
Đây là một trò chơi mang tính đồng đội rất cao, do đó mọi nhân viên đều có thể thảo luận chiến thuật trước khi chơi. Là một người cũng tham gia trò chơi này, hãy giúp tất cả mọi người đưa ra một chiến thuật chơi tối ưu và tìm ra dãy ~b~ có thứ tự từ điển nhỏ nhất có thể.
Một dãy ~a~ được gọi là có thứ tự từ điển nhỏ hơn dãy ~b~ khi và chỉ khi một trong hai điều sau đúng:
~a~ là tiền tố của ~b~, nhưng ~a \ne b~;
Tại vị trí đầu tiên mà ~a~ và ~b~ khác nhau, phần tử của dãy ~a~ nhỏ hơn phần tử của dãy ~b~.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên chứa số lượng test case ~t~ (~1 \leq t \leq 50~). Mô tả của mỗi test case như sau.
Dòng đầu chứa một số nguyên ~k~ (~0 \le k \le 16~). Ban đầu sẽ có ~2^k~ nhóm.
Dòng thứ hai chứa ~2^k~ số nguyên không âm ~a_1, a_2, \ldots, a_{2^k}~ ~(0 \le a_i \le 10^5)~ – số lượng nhân viên của mỗi nhóm.
Dòng cuối cùng nhập một dãy nhị phân ~s~ – danh sách hiệu lệnh của người quản trò. Kí tự ~s_i~ sẽ thể hiện hiệu lệnh thứ ~i~.
Dữ liệu đảm bảo rằng:
tổng ~|s|~ trong tất cả các testcase không quá ~10^5~, và
tổng số lượng vị trí sau cùng (độ dài dãy ~b~), trong tất cả các test không quá ~2^{16}~.
Output
Với mỗi testcase, in ra một dãy gồm ~2^h~ phần tử ~b_1, b_2, \ldots, b_{2^h}~ là dánh sách số lượng nhân viên của từng nhóm có thứ tự từ điểm nhỏ nhất khi trò chơi kết thúc.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~300~ | ~k \le 10~, tổng ~\vert s \vert~ trong tất cả các testcase không quá ~100~ |
| 2 | ~300~ | ~0 \le a_i \le 1~ trong mọi testcase |
| 3 | ~400~ | Không có giới hạn gì thêm |
| Total | ~1000~ |
Sample Input 1
2
1
4 2
10
1
4 2
01
Sample Output 1
4 2
0 6
Notes
Trong testcase đầu tiên, ban đầu có ~2^k = 2^1 = 2~ nhóm, với số lượng thí sinh thể hiện bởi dãy ~a = [4, 2]~. Dãy hiệu lệnh của người quản trò thể hiện bởi xâu ~s = \texttt{10}~.
Hiệu lệnh đầu tiên là hiệu lệnh ~1~, tức hiệu lệnh tách nhóm. Từ dãy ~a = [{\color{red}4}, {\color{blue}2}]~, người chơi có thể tạo thành các nhóm với dãy ~a = [{\color{red}1}, {\color{blue}1}, {\color{red}3}, {\color{blue}1}]~.
Hiệu lệnh thứ hai là hiệu lệnh ~0~, tưc hiệu lệnh gộp nhóm. Từ dãy ~a = [{\color{red}1}, {\color{blue}1}, {\color{red}3}, {\color{blue}1}]~, người chơi có thể tạo thành các nhóm với dãy ~a = [{\color{red}4}, {\color{blue}2}]~.
Điểm: 1750
Nằm trong lòng công nghiệp công nghệ sôi động, VNG đã khẳng định vị thế là một trong những công ty hàng đầu tại Việt Nam. Với cam kết xây dựng một môi trường làm việc tuyệt vời, VNG không chỉ chú trọng vào sự phát triển chuyên môn mà còn đặc biệt quan tâm đến sự cân bằng giữa công việc và cuộc sống cá nhân của nhân viên.
Để nâng cao sự hài lòng và năng suất của nhân viên, VNG thường xuyên tổ chức các hoạt động thú vị và thử thách, như những câu đố và trò chơi logic. Một trong những thử thách nổi bật mà công ty đưa ra là "Cái cân Hà Nội" – một trò chơi biến thể từ trò chơi Tháp Hà Nội.
Cái cân Hà Nội là một chiếc cân đĩa. Mỗi bên cân có một cái cọc, và ngoài ra có một cái cọc phụ nữa ở ngoài. Ban đầu, có một quả tạ với khối lượng ~s~ gram nằm ở cân phía bên phải. Cọc ở cân phía bên trái có chứa ~n~ đĩa tạ, lần lượt có khối lượng là ~2^0, 2^1, 2^2, \ldots, 2^{n - 1}~ gram theo thứ tự từ trên xuống dưới.
Được phép thực hiện thao tác sau không hoặc nhiều lần:
Chọn một cọc ~A~ đang có ít nhất một đĩa tạ.
Gọi quả cân trên cùng ở cọc ~A~ là ~x~.
Chọn một cọc ~B~ khác cọc ~A~ sao cho cọc ~B~ không chứa đĩa tạ nào có khối lượng nhỏ hơn đĩa tạ ~x~.
Di chuyển ~x~ từ cọc ~A~ sang cọc ~B~. Lúc này đĩa tạ trên cùng cọc ~B~ sẽ là ~x~.
Hãy tìm số lần di chuyển ít nhất sao cho đến cuối cùng:
Hai bên cân của cái cân Hà Nội cân bằng, và
mọi đĩa tạ đều nằm ở hai cọc trên cái cân Hà Nội.
Nếu không tồn tại cách di chuyển thỏa mãn, hãy chỉ ra điều đó.
Input
Đầu vào gồm nhiều bộ dữ liệu. Dòng đầu tiên của đầu vào chứa số nguyên ~t~ (~1 \le t \le 10\,000~) – số lượng bộ dữ liệu. Mô tả của mỗi bộ dữ liệu như sau.
Dòng đầu tiên và duy nhất của mỗi bộ dữ liệu gồm hai số nguyên ~s~ và ~n~ (~1 \le s \le 10^{18}~, ~1 \le n \le 60~) – khối lượng quả cân ở đĩa bên phải tính theo gram, và số lượng đĩa tạ nằm trên cọc ở đĩa cân bên trái.
Output
Với mỗi bộ dữ liệu, nếu như không tồn tại cách di chuyển làm cái cân Hà Nội cân bằng, hãy in ra ~-1~. Ngược lại hãy in ra một số nguyên duy nhất là số lần di chuyển ít nhất sao cho hai bên cân của cái cân Hà Nội cân bằng và mọi đĩa tạ đều nằm ở hai cọc trên cái cân Hà Nội.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~750~ | ~n \le 8~ |
| 2 | ~1000~ | Không có giới hạn gì thêm |
| Tổng | ~1750~ |
Sample Input 1
5
1 2
3 2
4 2
1 3
3 3
Sample Output 1
1
0
-1
3
3
Notes
Dưới đây là minh họa cho ví dụ đầu tiên:
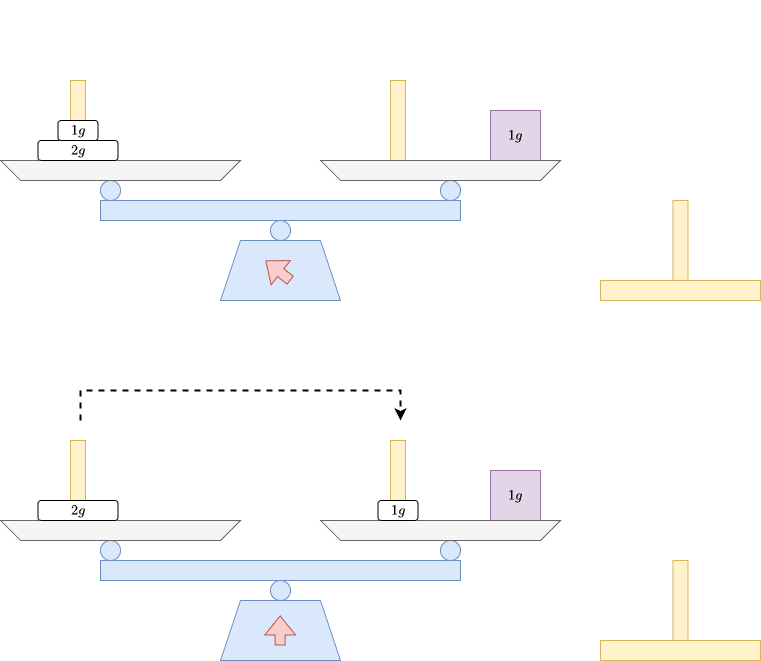
Ở ví dụ thứ hai, ở bên trái bao gồm đĩa tạ có khối lượng lần lượt là ~2^0~ và ~2^1~ gram, còn bên phải có quả cân có khối lượng ~3~ gram. Như vậy cái cân Hà Nội đã cân bằng, và ta không cần phải di chuyển tạ.
Ở ví dụ thứ ba, ở bên trái bao gồm đĩa tạ có khối lượng lần lượt là ~2^0~ và ~2^1~ gram, tổng cộng là ~3~ gram. Còn ở bên phải có quả cân có khối lượng ~4~ gram. Bên trái nhẹ hơn bên phải, do đó nếu ta di chuyển tạ thì không thể tăng được khối lượng ở đĩa cân bên trái. Vì vậy không có cách di chuyển hợp lệ.
Dưới đây là minh họa cho ví dụ thứ tư:
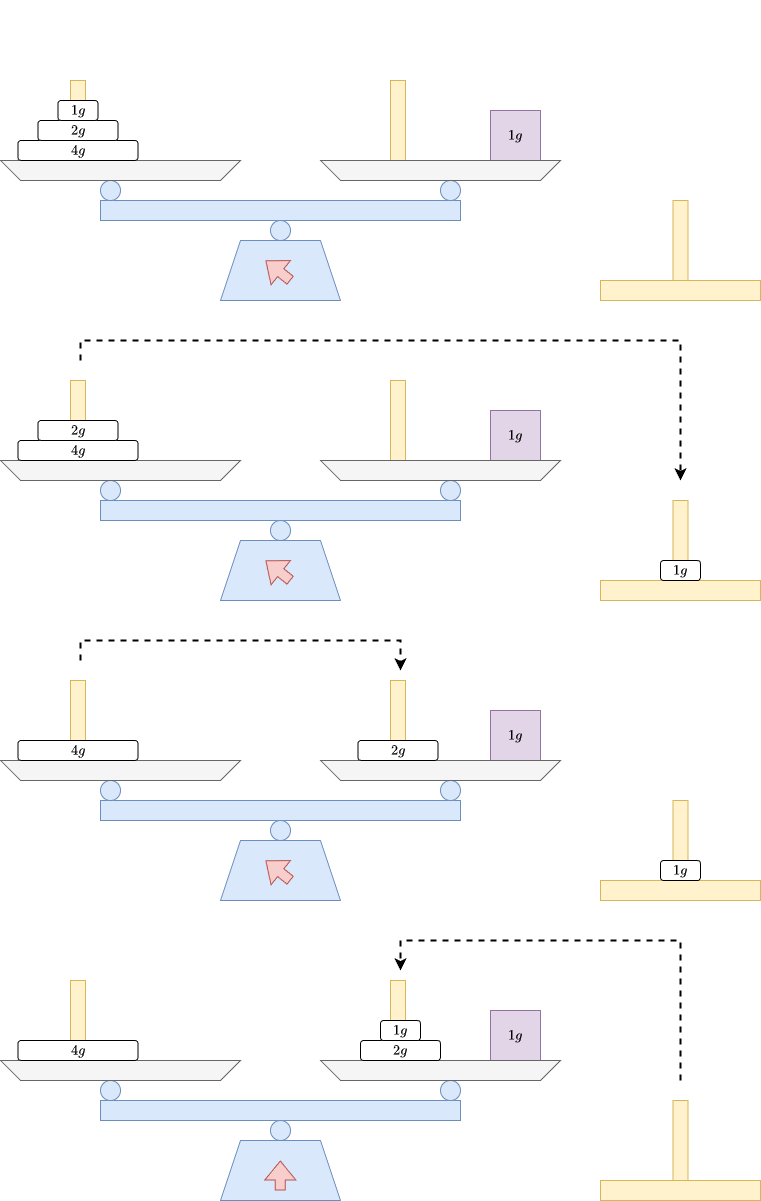
Dưới đây là minh họa cho ví dụ thứ năm:
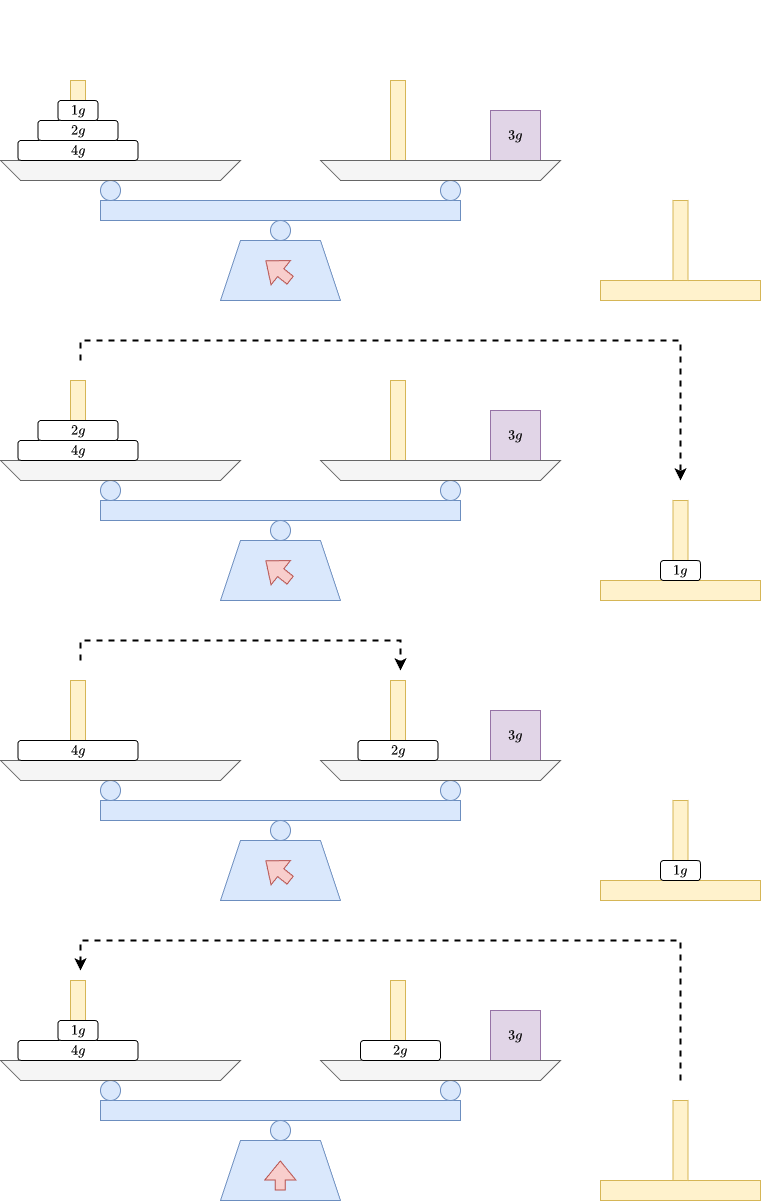
Điểm: 1750
"OK" là một cụm từ viết tắt phổ biến, thường được sử dụng để biểu đạt sự đồng ý, sự chấp nhận hoặc sự tán thành. Thậm chí người nói có thể lặp lại "OK" nhiều lần để nhấn mạnh sự tán thành. Để phủ định cụm từ này, trong tiếng Việt ta có thể thêm "không" vào đằng trước, và cụm từ này lại thường được viết tắt là "KO". Và ta có thể thêm nhiều "KO" vào trước để phủ định nhiều lần.
Như vậy một xâu có thể có ý nghĩa tán thành hoặc không tán thành. Ta định nghĩa sự tán thành của một xâu như sau:
Một xâu rỗng mang ý nghĩa tán thành;
Xâu có dạng ~\texttt{"OK"} + s~ sẽ có sự tán thành tương tự với xâu ~s~; cụ thể:
Xâu có dạng ~\texttt{"OK"} + s~ sẽ mang ý nghĩa tán thành, nếu ~s~ mang ý nghĩa tán thành;
Xâu có dạng ~\texttt{"OK"} + s~ sẽ mang ý nghĩa không tán thành, nếu ~s~ mang ý nghĩa không tán thành;
Xâu có dạng ~\texttt{"KO"} + s~ sẽ có sự tán thành ngược lại với xâu ~s~; cụ thể:
Xâu có dạng ~\texttt{"KO"} + s~ sẽ mang ý nghĩa tán thành, nếu ~s~ mang ý nghĩa không tán thành;
Xâu có dạng ~\texttt{"KO"} + s~ sẽ mang ý nghĩa không tán thành, nếu ~s~ mang ý nghĩa tán thành;
Các xâu không có dạng trên đều không có ý nghĩa.
Ví dụ:
~\texttt{""}~, ~\texttt{"OK"}~, ~\texttt{"KOKO"}~, ~\texttt{"KOKOOK"}~, ~\texttt{"KOOKKO"}~ và ~\texttt{"KOOKKOOK"}~ là các xâu tán thành.
~\texttt{"KO"}~, ~\texttt{"KOOK"}~, ~\texttt{"OKKO"}~, ~\texttt{"OKKOOK"}~, và ~\texttt{"KOOKKOKOOK"}~ là các xâu không tán tành.
~\texttt{"K"}~, ~\texttt{"O}~, ~\texttt{"KOO"}~, ~\texttt{"OKK"}~ và ~\texttt{"KOOOK"}~ là các xâu không có ý nghĩa.
Cho một xâu ~s~ chỉ gồm các kí tự ~\texttt{O}~ và ~\texttt{K}~. Ban đầu ~s~ chưa chắc đã mang ý nghĩa tán thành. Được phép chọn một vài kí tự trong ~s~ (các kí tự không nhất thiết phải liên tiếp, có thể không xóa kí tự nào). Ta cần thực hiện thao tác xóa để biến xâu ~s~ thành một xâu có ý nghãi tán thành.
Hãy đếm số cách xóa để thu được xâu mang ý nghĩa tán thành theo modulo ~10^9 + 7~.
Hai cách xóa được gọi là khác nhau nếu tồn tại một vị trí được xóa ở một cách, nhưng vị trí này không được xóa ở cách kia.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên chứa số lượng test case ~t~ (~1 \leq t \leq 10\,000~). Mô tả của mỗi test case như sau.
Dòng đầu tiên và duy nhất của test case chứa xâu ~s~ (~1 \le |s| \le 2 \cdot 10^5~) chỉ bao gồm các kí tự ~\texttt{O}~ và ~\texttt{K}~.
Đảm bảo rằng tổng của ~|s|~ qua tất cả các test case không vượt quá ~2 \cdot 10^5~.
Output
Với mỗi test case, in ra một số nguyên duy nhất là số cách xóa kí tự của xâu ~s~ để thu được xâu mang ý nghĩa tán thành, modulo ~10^9 + 7~.
Scoring
| Subtask | Score | Constraints |
|---|---|---|
| 1 | ~750~ | ~\vert s \vert \le 8~ với mọi test case |
| 2 | ~1000~ | Không có ràng buộc gì thêm |
| Total | ~1750~ |
Sample Input 1
4
KO
OK
KOOKO
KOKOKOKOKOKO
Sample Output 1
1
2
5
327
Notes
Ở test case thứ nhất, cách duy nhất là xóa hết toàn bộ xâu.
Ở test case thứ hai, có ~2~ cách là xóa hết xâu hoặc không xóa kí tự nào.
Ở test case thứ ba, có ~5~ cách tạo xâu mang ý nghĩa tán thành như sau (các kí tự gạch chân là các kí tự bị xóa):
~\underline{\texttt{KOOKO}}~ (xâu rỗng)
~\underline{\texttt{K}}\texttt{O}\underline{\texttt{O}}\texttt{K}\underline{\texttt{O}} \to \texttt{OK}~
~\underline{\texttt{KO}}\texttt{OK}\underline{\texttt{O}} \to \texttt{OK}~
~\texttt{KO}\underline{\texttt{O}}\texttt{KO} \to \texttt{KOKO}~
~\texttt{K}\underline{\texttt{O}}\texttt{OKO} \to \texttt{KOKO}~
Điểm: 2500
UpRace, dự án chạy bộ vì cộng đồng do VNG đề xuất, đang càng ngày càng có sức lan tỏa và ảnh hưởng trong cộng đồng. Năm nay, VNG đã đề xuất thêm một cuộc thi đặc biệt, Robot UpRace, nhằm khuyến khích phong trào tìm hiểu về trí tuệ nhân tạo và tự động hóa ở thế hệ trẻ Việt Nam.
Các robot sẽ tiến hành cuộc đua trên một lưới chữ nhật kích thước ~n \times n~. Các dòng được đánh số từ ~1~ đến ~n~, các cột cũng được đánh số từ ~1~ đến ~n~. Ô nằm tại dòng ~i~ và cột ~j~ được gọi là ô ~(i, j)~. Mỗi ô đều được ghi một số nguyên từ ~1~ đến ~n^2~.
Phần thi của một Robot sẽ bắt đầu khi robot xuất phát tại ô ~(1, 1)~, và sẽ kết thúc khi robot di chuyển đến ô ~(n, n)~. Ở mỗi bước, robot chỉ có thể đi đến một trong bốn ô kề cạnh với ô hiện tại. Robot không được phép di chuyển ra ngoài lưới chữ nhật. Ban tổ chức định nghĩa điểm số của một phần thi là số nguyên dương nhỏ nhất không xuất hiện tại các ô mà robot đi qua trong phần thi đó. Ban tổ chức sẽ xếp hạng các đội dựa vào điểm số của phần thi, điểm số càng nhỏ thì thứ hạng càng cao.
Hãy tìm điểm số nhỏ nhất có thể đạt được trong một phần thi.
Input
Bộ dữ liệu gồm nhiều test case. Dòng đầu tiên của bộ dữ liệu chứa số nguyên dương ~t~ (~1 \le t \le 100~) là số lượng test case. Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa số nguyên ~n~ (~2 \le n \le 2000~) — kích thước của lưới chữ nhật.
Dòng thứ ~i~ trong số ~n~ dòng tiếp theo gồm ~n~ số nguyên ~a_{i,1}, a_{i,2}, \ldots, a_{i,n}~ (~1 \le a_{i,j} \le n^2~) — các số được ghi tại các ô trên dòng ~i~.
Dữ liệu đảm bảo rằng tổng ~n^2~ trong tất cả các test case không quá ~4 \cdot 10^6~.
Output
Với mỗi test case, hãy in ra điểm số nhỏ nhất có thể đạt được trong một phần thi.
Scoring
| Subtask | Điểm | Ràng buộc |
|---|---|---|
| 1 | ~500~ | ~n \le 8~ |
| 2 | ~500~ | ~n \le 50~ |
| 3 | ~1500~ | Không có ràng buộc gì thêm |
| Tổng | ~2500~ |
Sample Input 1
2
3
3 1 2
1 3 2
1 1 4
2
2 3
3 4
Sample Output 1
2
1
Notes
Ở ví dụ thứ nhất, một trong số các phần thi có điểm số nhỏ nhất là ~(1, 1) \to (1, 2) \to (2, 2) \to (2, 1) \to (3, 1) \to (3, 2) \to (3, 3)~. Giá trị của các ô trên đường đi là ~[3, 1, 3, 1, 1, 1, 4]~, và điểm số của phần thi là ~2~.
Ở ví dụ thứ hai, một trong số các phần thi có điểm số nhỏ nhất là ~(1, 1) \to (1, 2) \to (2, 2)~. Giá trị của các ô trên đường đi là ~[2, 3, 4]~, và điểm số của phần thi là ~1~.
Điểm: 3250
Lưu ý: bài có giới hạn thời thời gian không bình thường.
Tập ~S~ là một tập hợp chứa các số nguyên không âm. Tập hợp này có một tính chất đặc biệt là nó có thể mang nhiều trạng thái chồng lập khác nhau sau mỗi biến đổi. Để giải thích kĩ hơn ta có thể nhìn vào hai thao tác biến đổi ~S~ sau:
"-" – xóa đi một phần tử của ~S~.
Ví dụ với tập ~S~ đang có duy nhất 1 trạng thái, và đang chứa phần tử ~\lbrace 1, 2, 3 \rbrace~, sau một thao tác "-", ~S~ có thể có 3 trạng thái là ~\lbrace 1, 2 \rbrace~, ~\lbrace 2, 3 \rbrace~ và ~\lbrace 1, 3 \rbrace~.
Nếu ta tiếp tục áp dụng thêm một thao tác "-" vào tập hợp, ~S~ lúc này sẽ có các trạng thái là ~\lbrace 1 \rbrace~, ~\lbrace 2 \rbrace~ và ~\lbrace 3 \rbrace~.
"+ ~x~" – thêm phần tử ~x~ vào ~S~.
Ví dụ, nếu như ~S~ đang có trạng thái ~\lbrace 1 \rbrace~ và ~\lbrace 2 \rbrace~, nếu ta áp dụng thao thao tác "+ 3", tập ~S~ sẽ mang các trạng thái ~\lbrace 1, 3 \rbrace~ và ~\lbrace 2, 3 \rbrace~.
Nếu như ta tiếp tục áp dụng thêm thao tác "+ ~1~", lúc này tập ~S~ sẽ mang các trạng thái ~\lbrace 1, 3 \rbrace~ và ~\lbrace 1, 2, 3 \rbrace~.
Hai thao tác trên có thể được kết hợp với nhau để tập ~S~ có nhiều trạng thái khác nhau. Ngoài ra khi áp dụng thao tác "-" vào ~S~, nếu hiện tại ~S~ đang có một trạng thái là rỗng thì trạng thái này sẽ được bỏ qua.
Ban đầu ~S~ có duy nhất một trạng thái là rỗng. Hãy thực hiện ~q~ truy vấn với tập ~S~, mỗi truy vấn thuộc một trong 3 thao tác sau:
"+ ~x~" – thao tác thêm phần tử vào ~S~;
"-" – thao tác xóa một phần tử khỏi ~S~;
"? ~k~" – hãy tìm số ~x~ lớn nhất có thể sao cho tồn tại một trạng thái của ~S~ mà ~x~ là phần tử lớn thứ ~k~ trong trạng thái đó, hoặc chỉ ra rằng không có trạng thái nào có ít nhất ~k~ phần tử.
Input
Dòng đầu tiên chứa một số tự nhiên ~q~ (~1 \le q \le 200\,000~) – số truy vấn cần xử lý.
Mỗi dòng trong ~q~ dòng tiếp theo sẽ thuộc một trong ba dạng sau:
"+ ~x~" (~1 \le x \le 200\,000~) – thao tác thêm phần tử vào ~S~.
"-' – thao tác xóa phần tử khỏi ~S~.
"? ~k~" (~1 \le k \le 10~) – truy vấn tìm số ~x~ lớn nhất có thể sao cho tồn tại một trạng thái của ~S~ mà ~x~ là phần tử lớn thứ ~k~ trong trạng thái đó.
Dữ liệu đảm bảo rằng tại mọi thời điểm, ~S~ lúc nào cũng có ít nhất một trạng thái.
Output
Với mỗi truy vấn loại "? ~k~", hãy in ra số ~x~ lớn nhất có thể sao cho tồn tại một trạng thái của ~S~ mà ~x~ là phần tử lớn thứ ~k~ trong trạng thái đó, hoặc in ra ~-1~ nếu không tồn tại trạng thái nào có ít nhất ~k~ phần tử.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~500~ | Không có hai sự kiện thêm quà nào có cùng giá trị ~x~. |
| 2 | ~750~ | ~k = 1~ |
| 3 | ~750~ | ~k \le 5~ |
| 4 | ~1250~ | Không có ràng buộc gì thêm. |
| Tổng | ~3250~ |
Sample Input 1
10
+ 5
+ 4
? 2
? 1
-
+ 5
? 2
? 1
-
? 2
Sample Output 1
4
5
4
5
-1
Sample Input 2
7
+ 3
+ 2
-
? 1
+ 3
-
? 1
Sample Output 2
3
3
Notes
Với ví dụ thứ nhất:
Sau hai thao tác đầu tiên, tập ~S~ sẽ có duy nhất một trạng thái là ~\lbrace 4, 5 \rbrace~
Tại truy vấn ? 2 đầu tiên, trạng thái duy nhất của ~S~ là ~\lbrace 4, 5 \rbrace~ có phần tử lớn thứ ~k = 2~ là ~4~, do đó đáp án là ~4~.
Tại truy vấn ? 1 ngay sau đó, tập ~S~ chưa có thay đổi gì. Đáp án là ~5~.
Tại truy vấn - đầu tiên, ~S~ sẽ mang các trạng thái ~\lbrace 4 \rbrace~ và ~\lbrace 5 \rbrace~.
Tại truy vấn + 5 ngay sau đó, ~S~ sẽ mang các trạng thái ~\lbrace 4, 5 \rbrace~ và ~\lbrace 5 \rbrace~.
Tại truy vấn ? 2 tiếp đó, ~S~ có duy nhất một trạng thái có hai phần tử là ~\lbrace 4, 5 \rbrace~. Đáp án là ~4~ do ~4~ là phần tử lớn thứ ~k = 2~ trong trạng thái này.
Tại truy vấn ? 1, cả hai trạng thái của ~S~ đều có phần tử lớn nhất là ~k = 5~.
Sau truy vấn - thứ hai, ~S~ sẽ không có trạng thái nào có ít nhất ~2~ phần tử, nên truy vấn ? 2 cuối cùng có đáp án là ~-1~.
Với ví dụ thứ hai:
Sau hai thao tác đầu tiên, tập ~S~ sẽ có duy nhất một trạng thái là ~\lbrace 2, 3 \rbrace~
Tại truy vấn - tiếp đó, tập ~S~ sẽ có các trạng thái ~\lbrace 2 \rbrace~ và ~\lbrace 3 \rbrace~.
Tại truy vấn ? 1 đầu tiên, trạng thái có phần tử lớn thứ ~k = 1~ lớn nhất là trạng thái ~\lbrace 3 \rbrace~. Đáp án là ~3~.
Tại truy vấn + 3 sau đó, tập ~S~ sẽ có các trạng thái ~\lbrace 2, 3 \rbrace~ và ~\lbrace 3 \rbrace~.
Tại truy vấn - sau đó, tập ~S~ sẽ có các trạng thái ~\lbrace 2\rbrace~, ~\lbrace 3 \rbrace~ và ~\lbrace \rbrace~ (trạng thái rỗng).
Tại truy vấn ? 1 cuối cùng, đán án là ~3~. Trạng thái có phần tử lớn thứ ~k = 1~ lớn nhất là ~\lbrace 3 \rbrace~.
UpRace Day là sự kiện chạy tập trung diễn ra trong khuôn khổ UpRace — dự án chạy bộ cộng đồng có sức ảnh hưởng lớn nhất Việt Nam. Sắp tới, Alpha sẽ là thành phố tiếp theo được lựa chọn để tổ chức sự kiện. Thành phố Alpha bao gồm ~n~ địa điểm được kết nối bởi ~n-1~ con đường hai chiều, đảm bảo giữa hai địa điểm bất kì luôn có đường đi đến nhau. Để sự kiện diễn ra suôn sẻ, thị trưởng thành phố đã lên kế hoạch vận chuyển ~m~ chuyến hàng phục vụ đồ ăn, nước uống và các vật dụng cần thiết. Chuyến hàng thứ ~i~ xuất phát từ địa điểm ~x_i~ và giao đến địa điểm ~y_i~. Chi phí để giao một chuyến hàng được tính bằng số con đường đi qua trên đường giao hàng. Mỗi chuyến hàng luôn lựa chọn tuyến đường có chi phí nhỏ nhất để di chuyển.
Nhận thấy thực trạng giao thông của thành phố còn nhiều hạn chế, thị trưởng đã gom góp hết ngân khố, cũng chỉ đủ để xây dựng thêm một con đường một chiều giữa hai địa điểm ~a~, ~b~ bất kì phục vụ riêng cho sự kiện đặc biệt này. Con đường này sẽ không tốn chi phí khi đi qua.
Bạn hãy giúp thị trưởng chọn con đường đường tốt nhất để xây dựng sao cho tiết kiệm được nhiều chi phí dành cho việc vận chuyển nhất.
Input
Mỗi test gồm nhiều test case. Dòng đầu tiên chứa số lượng test case ~t~ (~1 \leq t \leq 100~). Mô tả của mỗi test case như sau.
Dòng đầu tiên chứa hai số nguyên ~n~, ~m~ (~2 \leq n, m \leq 1500~) — số địa điểm trong thành phố Alpha và số chuyến hàng cần giao.
Dòng thứ ~i~ trong số ~n-1~ dòng tiếp theo chứa hai số nguyên ~u_i, v_i~ (~1 \leq u_i, v_i \leq n~) — hai địa điểm nối con đường thứ ~i~ của vương quốc.
Dòng thứ ~i~ trong ~m~ dòng tiếp theo chứa hai số nguyên ~x_i, y_i~ (~1 \leq x_i, y_i \leq n~) — địa điểm xuất phát và kết thúc của chuyến hàng thứ ~i~.
Dữ liệu đảm bảo rằng tổng ~n~ trong tất cả các testcase không vượt quá ~1500~, tổng ~m~ trong tất cả các testcase không vượt quá ~1500~.
Output
Với mỗi test case, in ra một số nguyên duy nhất là tổng chi phí nhỏ nhất để giao các chuyến hàng.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~500~ | Tổng ~n~ trong tất cả các testcase không vượt quá ~500~, tổng ~m~ trong tất cả các testcase không vượt quá ~500~. |
| 2 | ~1000~ | Mỗi địa điểm có tối đa hai đường nối tới các địa điểm khác. |
| 3 | ~2000~ | Không có giới hạn gì thêm. |
| Total | ~3500~ |
Sample Input 1
2
5 4
1 2
5 3
3 4
4 2
1 3
2 5
2 3
1 5
8 4
1 4
7 2
2 1
5 7
6 4
8 4
3 1
8 2
4 7
6 1
5 6
Sample Output 1
4
8
Notes
Trong ví dụ đầu tiên, thị trưởng sẽ xây dựng con đường nối từ địa điểm ~1~ đến địa điểm ~3~.

Sơ đồ thành phố cho ví dụ 1
Trong ví dụ thứ hai, thị trưởng sẽ xây dựng con đường nối từ địa điểm ~5~ đến địa điểm ~6~.
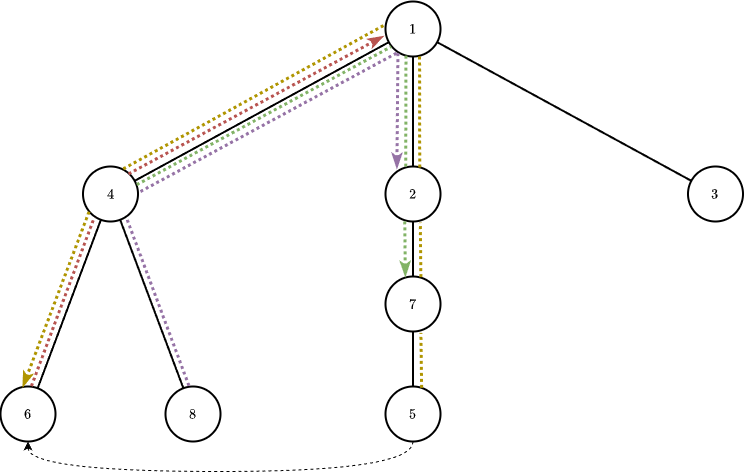
Sơ đồ thành phố cho ví dụ 2