Bạn có muốn tham gia nhận áo VNOI không?

Input

Gồm số nguyên không âm ~n~ duy nhất. ~(n \leq 100)~

Output

In ra dòng chữ "l want" và ~n~ dấu chấm than ở phía sau.

Sample Input

Sample Output

Bài chỉ được chấp nhận các ngôn ngữ C, C++ và Pascal

Vào ngày hè nắng nóng, sau khi giải xong 300 bài code thiếu nhi, Muối mở game lên và chơi nhưng do hay tải game lậu nên máy Muối đã bị nhiễm virus và hiện lên thông báo yêu cầu Muối phải giải được bài toán sau đây: Cho số nguyên không âm ~n~, gọi tích ~n~ số nguyên không âm ~a_i~ là ~G~, bội chung nhỏ nhất ~n~ số nguyên không âm ~a_i~ là ~F~, hãy tính ~\frac{G}{F}~. Vì đã khá mệt sau khi giải nhiều bài, Muối cần bạn giúp.

Input

• Dòng đầu tiên, chứa số ~n~.
• Dòng thứ hai, chứa ~n~ số ~a_i~ ( ~a_i \le 10^7~ ).

Output

• Một dòng chứa số nguyên duy nhất là đáp án. Nếu không có đáp án in ra ~impossible~. Dữ liệu đảm bảo đáp án không lớn hơn ~10^{18}~

Sample Input 1

3
1 2 3

Sample Output 1

1

Subtask

• ~50\%~ số test có ~n \le 21~
• ~50\%~ số test còn lại có ~n \le 100~

Giải thích ví dụ

Ở ví dụ, ta có: ~G~ = ~1 \times 2 \times 3 = 6~, ~F~ = ~6~ => ~\frac{G}{F}~ = ~\frac{6}{6}~ = ~1~ .

Cho một mảng ~A~ gồm ~N~ số nguyên. Như bạn đã biết, trên mảng này có tổng cộng ~\frac{N(N + 1)}{2}~ đoạn con liên tiếp. Bạn được yêu cầu in ra đoạn con liên tiếp có tổng lớn thứ ~K~ (Đoạn con liên tiếp có tổng lớn thứ 1 là đoạn con liên tiếp có tổng lớn nhất mảng).

Input

Dòng đầu tiên gồm hai số nguyên ~N~ và ~K~ ~(1 \le N \le 10^5)~ ~(1 \le K \le \frac{N(N + 1)}{2})~.

Dòng thứ hai gồm ~N~ số nguyên mô tả mảng ~A~ ~(-10^9 \le A_i \le 10^9)~.

Output

In ra một số nguyên duy nhất là giá trị của đoạn con liên tiếp có tổng lớn thứ ~K~.

Sample Input 1

3 1
1 2 3

Sample Output 1

6

Sample Input 2

3 1
-1 -2 -3

Sample Output 2

-1

Subtask

• ~50\%~ số test có ~N \le 1000~
• ~50\%~ số test còn lại không có điều kiện gì thêm

Chắc hẳn các bạn ai cũng đã từng chơi trò dò mìn (Minesweeper). Trong trò chơi này, người chơi khởi đầu với một bảng ô vuông trống thể hiện bãi mìn. Người chơi sẽ phải click chuột vào một trong số các ô vuông trong bảng.

Nếu không may trúng phải ô có mìn thì trò chơi kết thúc. Trường hợp khác là ô đó không có mìn và một vùng các ô sẽ được mở ra cùng với những con số. Số trên một ô là số lượng mìn có trong ~8~ ô nằm quanh ô đó.

Một bảng mìn có thể có dạng như sau:

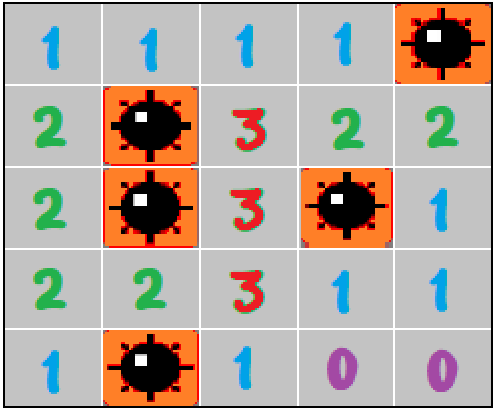
Bạn được cho một ma trận ~n \times m~ , mỗi ô chứa số ~0~ hoặc ~1~ lần lượt đại diện cho ô không có mìn và ô có mìn. Bạn hãy tìm một ma trận ~01~ khác có cùng kích thước sao cho tổng giá trị các số trong các ô không có mìn của nó bằng với ma trận ban đầu. (Số trên một ô không mìn là số lượng mìn có trong ~8~ ô nằm xung quanh ô đó)

Input

• Dòng đầu tiên chứa ~2~ số nguyên dương ~n,m~ là kích thước của ma trận.

• ~n~ dòng tiếp theo, mỗi dòng chứa ~m~ số nguyên là giá trị các ô trong ma trận.

Output

• Một ma trận ~n \times m~ khác thỏa mãn yêu cầu đề bài.

(Nếu có nhiều ma trận thỏa mãn, in ra bất kỳ. Ngược lại, nếu không tìm được ma trận thỏa mãn, in ra ~-1~.

Sample Input

4 5
0 1 0 1 1
0 0 0 1 0
1 0 0 0 0
0 0 1 0 0

Sample Output

0 0 0 0 0 
1 1 0 1 0 
0 1 1 1 0 
1 1 1 1 0

Giải thích ví dụ:

Ma trận input mô tả bãi mìn sau:

Ma trận output mô tả bãi mìn sau:

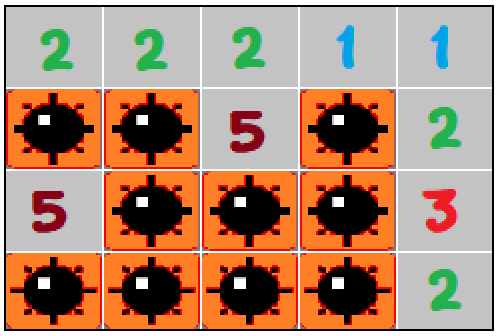
Tổng các số trong những ô không có mìn ở cả ~2~ ma trận đều là ~25~.

Subtask

• Có ~40\%~ số lượng test thỏa mãn điều kiện: ~n \times m \leq 20~.

• ~20\%~ khác thỏa mãn: ~n = 1, m \leq 10^{3}~.

• ~40\%~ số test còn lại thỏa mãn: ~n, m \leq 7 \cdot 10^{3}~ và ~n \times m \leq 10^{6}~.

Bạn được cho một mảng ~a~ gồm ~n~ số nguyên dương, mỗi phần tử ban đầu được bọc trong một "phản tế bào". Mỗi phản tế bào có thế chứa nhiều phần tử liên tiếp nhau, tuy nhiên theo định nghĩa trên thì ban đầu mỗi phản tế bào chỉ chứa một phần tử. Trái với việc phân chia của một tế bào thành hai tế bào con giống nhau, hai phản tế bào cạnh nhau có thể ghép lại thành một phản tế bào lớn hơn với toàn bộ phần tử từ hai phản tế bào này nếu tổng các phần tử trong hai phản tế bào này là như nhau.

Bạn cũng nhận được một dãy ~b~ rỗng, và một số nguyên dương ~i~ được gán bằng ~1~. Nhiệm vụ của bạn là thay đổi dãy ~b~ sử dụng các thao tác sau:

• Nếu ~i = n + 1~, dừng thao tác thay đổi dãy ~b~.
• Xét phản tế bào đang chứa phần tử ~a_i~ (gọi là ~X~), và phản tế bào liền kề trước ~X~ (gọi là ~Y~). Bạn được quyền lựa chọn việc ghép ~X~ và ~Y~ nếu như ~Y~ tồn tại và tổng các phần tử trong ~X~ bằng tổng các phần tử trong ~Y~. Lưu ý là nếu cả hai điều kiện là hợp lệ, bạn có thể chọn ghép hoặc không ghép hai phản tế bào này.
• Nếu bạn chọn không ghép (hoặc bạn không thể ghép) ~X~ và ~Y~, tăng ~i~ lên ~1~.
• Nếu bạn chọn ghép ~X~ và ~Y~, ghép hai phản tế bào lại và thêm ~i~ vào đuôi của ~b~. Lưu ý ta không tăng ~i~ nếu chọn ghép.

Ta có thể chứng minh thao tác trên sẽ luôn kết thúc (tức sau hữu hạn bước ta sẽ có ~i = n + 1~). Bạn cần đếm có bao nhiêu dãy ~b~ khác nhau có thể tạo được sử dụng các thao tác này. Hai dãy ~c~ và ~d~ khác nhau nếu ~|c| \ne |d|~ hoặc tồn tại một vị trí ~i~ sao cho ~c_i \ne d_i~.

Input

Dòng đầu tiên chứa số nguyên dương ~n~ (~1 \le n \le 2 \cdot 10^5~) - số lượng phần tử trong ~a~.

Dòng thứ hai chứa ~n~ số nguyên dương ~a_1, a_2, a_3, \dots, a_n~ (~1 \le a_i \le 10^9~) - các phần tử trong ~a~.

Output

Ghi ra số lượng dãy ~b~ khác nhau có thể tạo được từ các thao tác đã cho. Vì số lượng dãy ~b~ có thể rất lớn, ghi ra con số này dưới modulo ~10^9 + 7~.

Sample Input

4
1 1 1 1

Sample Output

6

Subtask

• ~20\%~ số test có ~n \le 20~
• ~80\%~ số test còn lại không có điều kiện gì thêm

Note

Một ví dụ về dãy ~b~ có thể tạo được như sau. Các phản tế bào sẽ được đánh nhau bằng các phần tử giữa ngoặc vuông.

• ~a = [1][1][1][1]~, ~i=1~, ~b=[]~, không thể ghép vì không tồn tại ~Y~.
• ~a = [1][1][1][1]~, ~i=2~, ~b=[]~, chọn ghép hai phản tế bào ~[1]~ và ~[1]~.
• ~a = [1, 1][1][1]~, ~i=2~, ~b=[2]~, không thể ghép vì không tồn tại ~Y~.
• ~a = [1, 1][1][1]~, ~i=3~, ~b=[2]~, không thể ghép vì ~[1, 1]~ và ~[1]~ không cùng tổng.
• ~a = [1, 1][1][1]~, ~i=4~, ~b=[2]~, chọn ghép hai phản tế bào ~[1]~ và ~[1]~.
• ~a = [1, 1][1, 1]~, ~i=4~, ~b=[2, 4]~, chọn không ghép hai phản tế bào ~[1, 1]~ và ~[1, 1]~.
• ~a = [1, 1][1, 1]~, ~i=5~, ~b=[2, 4]~, kết thúc thao tác. Dãy ~b~ cuối cùng là ~[2, 4]~.