Bedao OI Contest 3 - Day 2
Điểm: 7
Ở khu xóm "Tà tưa" có ~n~ ngôi nhà. Các ngôi nhà được kết nối với nhau bởi ~m~ con đường hai chiều có độ dài khác nhau. Từ một ngôi nhà bất kì, ta có thể đến được các ngôi nhà còn lại.
Người dân ở đây đều là những người nghiện trà sữa, do đó đã có ~k~ nhà tự mở quán trà sữa để phục vụ xóm làng. Họ muốn biết khoảng cách để tới quán trà sữa gần nhất. Với những ngôi nhà tự mở quán, có một vài người không muốn uống ở nhà nên sẽ tìm quán gần nhất khác quán của mình.
Yêu cầu: Với từng ngôi nhà, cho biết khoảng cách ngắn nhất để đi tới một quán trà sữa.
Input
Dữ liệu vào từ file văn bản milktea.inp
Dòng đầu tiên gồm ba số nguyên ~n, m, k~ (~2 \le k \le n \le 10^5, n - 1 \le m \le min(\frac{n \times (n-1)}{2}, 2 \times 10^5~)) — lần lượt là số ngôi nhà, số con đường và số quán trà sữa.
~m~ dòng tiếp theo, mỗi dòng gồm ba số nguyên ~u, v, w~ (~1 \le u, v \le n, 1 \le w \le 10^9~) — mô tả một con đường hai chiều nối hai ngôi nhà ~u~ và ~v~ với độ dài ~w~. Đầu vào đảm bảo không có con đường nào nối một ngôi nhà tới chính nó, cũng như không tồn tại hai con đường nối cùng một cặp ngôi nhà.
~k~ dòng tiếp theo, mỗi dòng gồm hai số nguyên ~p_i~ và ~t_i~ (~1 \le p_i \le n, t_i \in \{0, 1\}~) — mô tả quán trà sữa thứ ~i~. Nếu ~t_i = 1~ thì người ở nhà ~p_i~ cần tìm một quán trà sữa khác ~p_i~ để uống, ngược lại nếu ~t_i = 0~ thì có thể uống luôn tại nhà. Đầu vào đảm bảo các số ~p_i~ là phân biệt đôi một.
Output
Kết quả in ra file văn bản milktea.out
- Gồm một dòng chứa ~n~ số nguyên ~d_1, d_2, \dots, d_n~, với ~d_i~ là khoảng cách từ ngôi nhà thứ ~i~ đến quán trà sữa gần nhất.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~20~ | ~2 \le n \le 1\,000~ |
| 2 | ~20~ | ~t_i = 0~ ~\forall i: 1 \le i \le k~ |
| 3 | ~25~ | ~m = n - 1~ |
| 4 | ~35~ | Không có ràng buộc gì thêm |
Sample Input 1
5 6 2
1 2 3
2 4 6
5 3 4
1 3 5
3 4 2
4 5 9
1 0
5 1
Sample Output 1
0 3 4 6 9
Notes
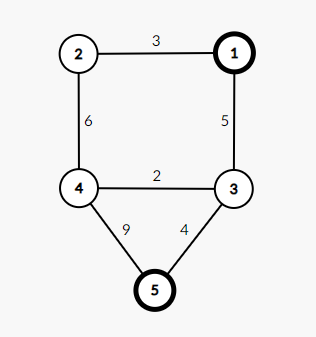
Mô tả ví dụ.
Trong ví dụ trên, có ~2~ quán trà sữa đặt tại các nhà ~1~ và ~5~. Người ở nhà ~1~ có thể uống trà sữa ngay tại nhà nên ~d_1 = 0~, còn người ở nhà ~5~ phải đi đến quán trà sữa ở nhà ~1~ theo con đường ~5 \rightarrow 3 \rightarrow 1~.
Điểm: 7
Cho một xâu ~S~ gồm các chữ cái Latinh viết hoa, một số nguyên dương ~C~ và một dãy gồm ~|S|~ phần tử ~A_1, A_2, \cdots, A_{|S|}~.
Xuất phát tại một vị trí ~1 \le i \le |S|~, hãy tìm chi phí nhỏ nhất để di chuyển và biến đổi xâu ~S~ thành palindrome.
Biết rằng từ vị trí ~i~ di chuyển tới ~i - 1~ hoặc ~i + 1~ sẽ tốn ~C~ chi phí. Tại một vị trí ~j~ bất kì, ta được phép biến đổi ~S_j~ thành bất cứ kí tự nào với chi phí là ~A_j~.
In ra chi phí nhỏ nhất với mọi vị trí.
Input
Dữ liệu vào từ file văn bản palin.inp:
Dòng đầu tiên chứa số nguyên ~T~ (~1 \le T \le 1000~) — Số test. Với mỗi test:
Dòng đầu tiên của test chứa xâu ~S~ (~1 \le |S| \le 10^6~) — Xâu ~S~ chỉ gồm các chữ cái Latin viết hoa.
Dòng tiếp theo chứa số nguyên dương ~C~ (~1 \le C \le 10^9~) — Chi phí một bước di chuyển.
Dòng cuối cùng chứa ~|S|~ số nguyên ~A_1, A_2, \cdots, A_n~ (~1 \le A_i \le 10^9~) — Chi phí một phép biến đổi của mỗi vị trí.
Dữ liệu đảm bảo tổng ~|S|~ của tất cả các test không vượt quá ~10^6~.
Output
Dữ liệu in ra file văn bản palin.out:
Với mỗi test, trên một dòng in ra ~|S|~ số nguyên là chi phí nhỏ nhất để biến đổi xâu ~S~ thành palindrome với mọi vị trí.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~10\%~ | Tổng ~|S| \le 40~ |
| 2 | ~20\%~ | Tổng ~|S| \le 500~ |
| 3 | ~20\%~ | Tổng ~|S| \le 5000~ |
| 4 | ~50\%~ | Không có ràng buộc gì thêm |
Sample Input 1
2
ABCDE
1
7 1 4 5 1
ABCDA
1
7 1 4 5 1
Sample Output 1
6 5 6 6 5
2 1 2 3 4
Notes
Ở ví dụ thứ nhất, bắt đầu ở vị trí ~1~, một trong những cách tối ưu là di chuyển sang vị trí ~2~ tốn ~1~, đổi "B" thành "D" tốn ~1~, sau đó di chuyển đến vị trí ~5~ tốn ~3~ và đổi "E" thành "A" tốn ~1~. Tổng cộng là ~6~.
Điểm: 6
Do quá đam mê bộ truyện tranh trinh thám "Thám tử lừng danh Conan", đặc biệt là hâm mộ nhân vật siêu trộm Kaito Kid, ba anh chàng Giang, Tâm và Thắng đã bàn nhau kế hoạch đột nhập vào ngân hàng đề thi quốc tế và cuỗm đi bộ đề thi của kì thi ICPC World Final. Sau một thời gian tìm hiểu, Giang đã phân tích và phát hiện ra rằng cấu trúc của khóa cửa ngân hàng đề thi được thiết kế vô cùng đặc biệt.
Khóa mỗi chiếc cửa là một bảng có kích thước ~R~ hàng, ~C~ cột. Để mở khóa của mỗi cửa, người mở cần chiếu một tia laser vào hàng trên cùng theo hướng từ trái sang phải. Trên bảng người ta thiết kế các tấm gương (~\backslash~ và ~/~ - những tấm gương được đặt ở góc chéo ~45^{\circ}~) để làm thay đổi quỹ đạo của tia laser một góc ~90^{\circ}~. Cửa sẽ được mở ra nếu tia laser đi ra khỏi hàng cuối cùng của bảng theo hướng từ trái sang phải.
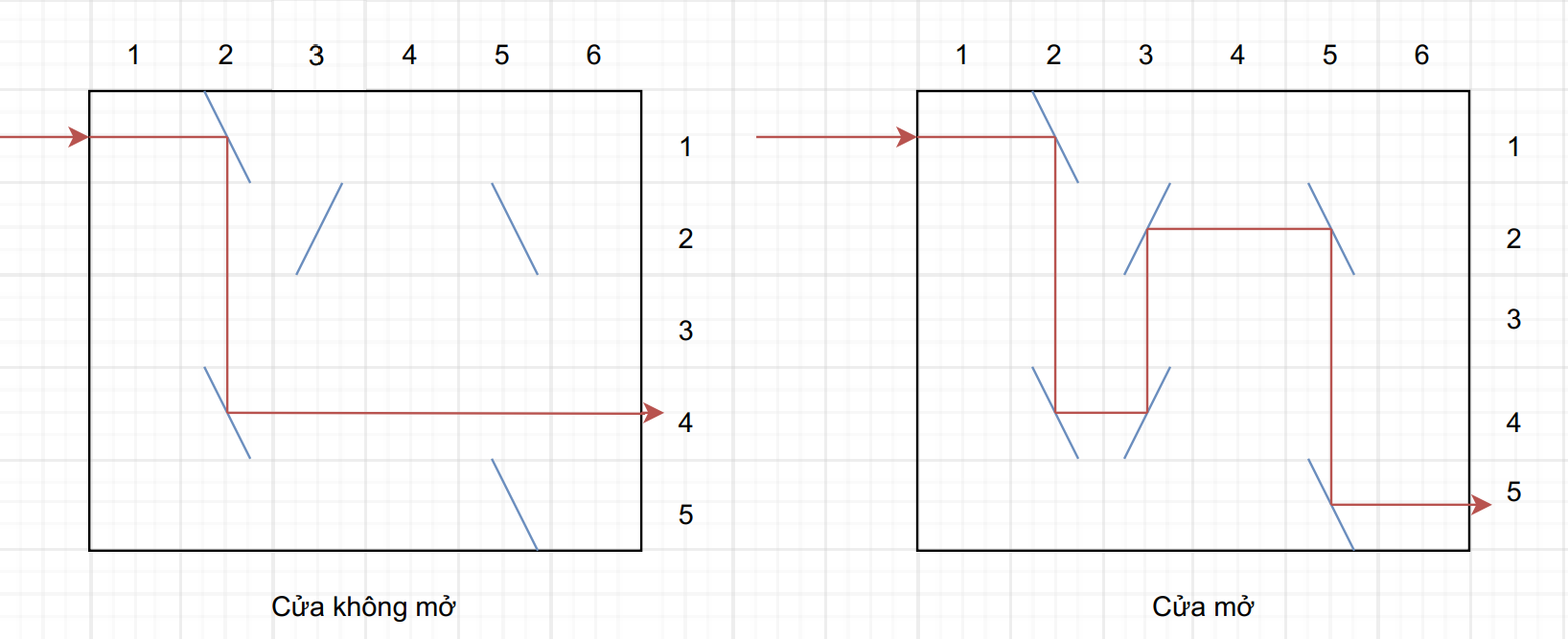
Để tăng độ bảo mật, nhà sản xuất có thể bỏ bớt một tấm gương trong bảng để chỉ người nắm giữ quyền hạn mới biết cách thêm tấm gương vào đúng vị trí để mở cửa. Để tiến đến được nơi cất giữ đề thi, nhóm trộm cần vượt qua hàng loạt cửa khác nhau. Bằng tài năng dự đoán, Tâm và Thắng đã vẽ ra được sơ đồ của toàn bộ những cánh cửa mà họ cần vượt qua. Điều khó khăn duy nhất hiện tại là tìm cách để mở khóa một số cánh cửa được bảo mật (những cách cửa bị thiếu một tấm gương) hoặc phát hiện những cánh cửa bị sản xuất lỗi và không có cách để mở cửa bằng cách thêm tấm gương.
Mặc dù có rất nhiều tài năng nhưng đối mặt với bài toán hóc búa này ba chàng trai cần sự trợ giúp từ cộng đồng VNOI. Các bạn hãy giúp họ thực hiện việc đó nhé!
Input
Dữ liệu vào từ file văn bản laser.inp:
Gồm nhiều nhóm dữ liệu (có tối đa ~10~ nhóm dữ liệu), trong đó mỗi nhóm dữ liệu mô tả sơ đồ của một cửa mà nhóm cần vượt qua:
Dòng đầu tiên gồm ~4~ số nguyên dương ~R~, ~C~, ~M~ và ~N~ (~1 \le R, C \le 1\ 000\ 000~ và ~0 \le M, N \le 200\ 000~) - lần lượt là số dòng, số cột của bảng và số vị trí đặt tấm gương '~/~' và '~\backslash~'.
~M~ dòng tiếp theo, mỗi dòng chứa ~2~ số nguyên dương ~x_i~,~y_i~ (~1 \le x_i \le R~, ~1 \le y_i \le C~) - là tọa độ của các tấm gương ~/~.
~N~ dòng tiếp theo, mỗi dòng chứa ~2~ số nguyên dương ~x_i~,~y_i~ (~1 \le x_i \le R~, ~1 \le y_i \le C~) - là tọa độ của các tấm gương ~\backslash~.
Dữ liệu đảm bảo tọa độ của ~M + N~ tấm gương là đôi một phân biệt.
Output
Kết quả in ra file văn bản laser.out:
Với mỗi nhóm dữ liệu, in ra đáp án trên một dòng:
In ra ~0~ nếu chiếc cửa đó có thể mở mà không cần thêm bất cứ tấm gương nào.
In ra ~k~ ~r~ ~c~ nếu cần thêm một tấm gương để mở được cánh cửa, trong đó có chính xách ~k~ vị trí có thể thêm tấm gương vào để mở cửa và ~(r, c)~ là vị trí có thứ tự từ điển nhỏ nhất. Nếu ở một tọa độ ~(x,y)~ mà tồn tại ~2~ cách thêm tấm gương khác nhau thì chỉ tính ~1~ lần.
In ra ~impossible~ nếu không tồn tại cách nào thêm tấm gương để mở được cửa.
Một điểm ~(x_1, y_1)~ được coi là có thứ tự từ điển nhỏ hơn điểm ~(x_2, y_2)~ nếu ~x_1 < x_2~ hoặc ~x_1 = x_2~ và ~y_1 < y_2~.
Scoring
| Subtask | Điểm | Giới hạn |
|---|---|---|
| 1 | ~10~ | ~R = 1~ hoặc ~C = 1~ hoặc ~N = 0~ |
| 2 | ~40~ | ~M, N \le 2000~ |
| 3 | ~50~ | Không có ràng buộc gì thêm. |
Sample Input 1
5 5 1 4
2 3
1 2
2 5
4 2
5 5
10 10 0 2
1 8
10 8
1000000 1000000 0 0
Sample Output 1
2 4 3
0
impossible